
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямые измерения с многократными наблюдениями
Обработка результатов наблюдений производится в следующей последовательности: 1. Исключить известные систематические погрешности из результатов наблюдений (введением поправки). 2. Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения:
3. Вычислить оценку среднего квадратического отклонения (СКО) результатов наблюдений
Вычислив оценку СКО результата наблюдений, целесообразно проверить наличие в группе наблюдений грубых погрешностей, помня, что при нормальном законе распределения ни одна случайная погрешность 4. Вычислить оценку СКО результата измерения
5. Проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению. Приближенно о характере распределения можно судить, построив гистограмму. Строгие методы проверки гипотез осуществляются с использованием специальных критериев ( При числе наблюдений 6. Вычислить доверительные границы
где 7. Вычислить границы суммарной неисключенной систематической погрешности (НСП) результата измерений. Неисключенная систематическая погрешность результата образуется из неисключенных систематических погрешностей метода, средств измерений, погрешностей поправок и др. При суммировании эти составляющие рассматриваются как случайные величины. При отсутствии данных о виде распределения неисключенных составляющих систематических погрешностей их распределения принимают за равномерные. При равномерном распределении неисключенных систематических погрешностей границы неисключенной систематической погрешности результата измерения
где Доверительную вероятность для вычисления границ НСП принимают той же, что при вычислении границ случайной погрешности результата измерения. 8. Вычислить доверительные границы погрешности результата измерения. Анализ соотношения между неисключенной систематической погрешностью и случайной погрешностью показывает, что если Если оба неравенства не выполняются, вычисляют СКО результата как сумму неисключенной систематической погрешности и случайной составляющей: Границы погрешности результата измерения в этом случае вычисляют по формуле
Коэффициент
Стандартом регламентирована и форма записи результатов измерений. При симметричном доверительном интервале погрешности результат измерения представляют в форме При отсутствии данных о видах функции распределения составляющих погрешности результата или при необходимости дальнейшей обработки результатов, результат измерения представляют в форме
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.218.147 (0.008 с.) |
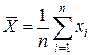 .
.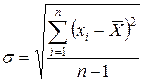 .
.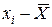 , с вероятностью практически равной единице, не может выйти за пределы
, с вероятностью практически равной единице, не может выйти за пределы 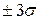 . Наблюдения, содержащие грубые погрешности, исключают из группы и заново повторяют вычисления
. Наблюдения, содержащие грубые погрешности, исключают из группы и заново повторяют вычисления 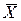 и
и 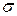 .
.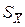 по формуле
по формуле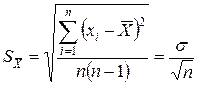 .
.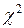 - Пирсона,
- Пирсона, 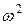 -Мизеса-Смирнова и др.).
-Мизеса-Смирнова и др.).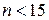 принадлежность их к нормальному распределению не проверяют, а доверительные границы случайной погрешности результата определяют лишь в том случае, если достоверно известно, что результаты наблюдений принадлежат нормальному закону.
принадлежность их к нормальному распределению не проверяют, а доверительные границы случайной погрешности результата определяют лишь в том случае, если достоверно известно, что результаты наблюдений принадлежат нормальному закону.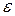 случайной погрешности результата измерения при заданной вероятности
случайной погрешности результата измерения при заданной вероятности 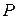 :
: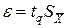 ,
,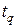 - коэффициент Стьюдента.
- коэффициент Стьюдента.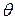 вычисляют по формуле
вычисляют по формуле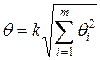 , (7)
, (7) 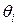 - граница
- граница 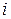 - й неисключенной составляющей систематической погрешности;
- й неисключенной составляющей систематической погрешности; 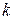 - коэффициент, определяемый принятой доверительной вероятностью (при
- коэффициент, определяемый принятой доверительной вероятностью (при 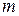 - количество неисключенных составляющих.
- количество неисключенных составляющих.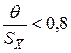 , то неисключенной систематической погрешностью можно пренебречь и принять границы погрешности результата
, то неисключенной систематической погрешностью можно пренебречь и принять границы погрешности результата 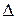 равным
равным 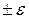 . Если
. Если 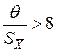 , то случайной погрешностью можно пренебречь и принять границы погрешности результата равным
, то случайной погрешностью можно пренебречь и принять границы погрешности результата равным  .
.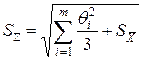 . (8)
. (8) 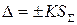 .
.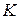 вычисляют по эмпирической формуле
вычисляют по эмпирической формуле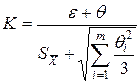 .
.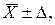
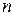 ,
, 


