Второе положение - так называемый закон радиуса.

Обращает на себя внимание не только спекулятивный характер этого закона, но и то обстоятельство, что Кеплер вообще искал такого рода закономерности, оставив попытки построения эквантной окружности. Тем самым он уже отошел от аксиомы Платона, то есть от утверждения, что планеты движутся с постоянной угловой скоростью. Определяющим здесь было его мистическое отношение к Солнцу. Воображаемые точки, вокруг которых, как считалось, вращаются небесные тела, были для него чем-то призрачным. Его тревожило уже то, что в системе Коперника Солнце на самом деле не находилось в центральной точке (и потому она не могла быть названа "гелиоцентрической" в строгом смысле) [47] и выполняло лишь вспомогательную роль источника света. Для Кеплера же Солнце представляло собой священный центр Вселенной, воплощение Бога-Отца. Поэтому от Солнца должна была исходить сила, заставлявшая планеты кружиться вокруг него (Кеплер связывал ее со Святым Духом, а неподвижные звезды - с Богом-Сыном). Поэтому так важно было определить эту силу, и поэтому вычислению подлежало движение планет по отношению именно к Солнцу, а не к воображаемой точке в пространстве.

Именно эта страстная убежденность в гелиоцентризме дала Кеплеру возможность искать и находить нечто вроде закона радиуса, а непоколебимая уверенность, выросшая на почве возрожденческого гуманизма, в том, что принципы устройства Вселенной постижимы для человеческого разума, придавала ему смелость, позволявшую видеть в рискованных экстраполяциях силу доказательства. Вдохновляемый своей философией, он неотступно продвигался вперед, приступив к решению задачи, которая не могла не казаться аристотелианцам изумительной дерзостью - связать закон радиуса с принципом рычага, а затем с гильбертовским магнетизмом, тем самым связывая небесные и земные движения. Отсюда уже было недалеко до воззрения на Вселенную не как на подобие божественной формы жизни (instar divine animalis), а как на подобие часового механизма (instar horologii) ^[48]. Однако в своей гипотезе о причинах движения планет, которую можно было бы рассматривать как предвосхищение теории тяготения Ньютона, он вновь возвращается к аристотелизму, абсолютно противопоставляя покой и движение (он полагал, что если бы не сила, генерируемая Солнцем, то движение планет из-за их естественной инерции остановилось бы). Это закрывало ему путь к закону инерции и, следовательно, как мы теперь понимаем, к наиболее важному аргументу в пользу идеи Коперника.

После размышлений над небесной механикой он вернулся к теории движения Марса. Рассмотрим рис. 2.

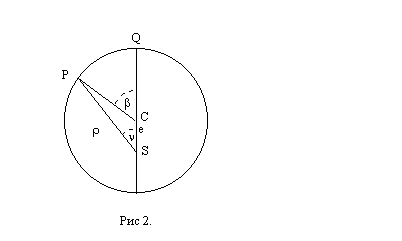
По закону радиуса скорость планеты в точке P на орбите с центром C обратно пропорциональна расстоянию = PS до Солнца S: следовательно, время, затрачиваемое на движение в этом сегменте, пропорционально PS. Но как выразить эту зависимость точной формулой? Казалось невозможным найти прямое отношение между радиусом и временем движения. И здесь Кеплер вспомнил так называемую теорему Архимеда, выражающую отношение площади круга и радиуса окружности. Согласно этой теореме площадь сектора QCP можно рассматривать как предел суммы бесконечного числа бесконечно малых треугольников с высотой, равной радиусу окружности. Это подсказало Кеплеру идею связать время, за которое планета проходит путь PQ, не непосредственно с радиусом окружности, а с площадью сектора, описываемого радиус-вектором. Не долго думая, он применил теорему Архимеда, благодаря чему в его распоряжении оказалось достаточно сомнительное средство выражения через площадь, описываемую отрезком CP (то есть радиус-вектором орбиты) времени, необходимого для прохождения планетой соответственной дуги орбиты, и тем самым он получил по крайней мере косвенную возможность выразить соотношение времени и радиус-вектора в следующей формуле:

(1)

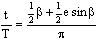
где t - время прохождения планетой дуги PQ, а Т - время, затрачиваемое планетой на прохождение всей орбиты. Если r = 1, то площадь QCP = 1/2, площадь CSP = 1/2 e sin, а - площадь круга.

Из (1) следует:

(2)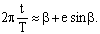