
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практическое применение интерференции светаСодержание книги
Поиск на нашем сайте
Явление интерференции находит широкое практическое применение. Исследуя, например, интерференционную картину «полосы равной толщины» можно измерять малые углы клиновых деталей, диаметры очень тонких проволочек, а также контролировать качество обработки поверхности (ведь мельчайшая шероховатость на поверхности клина приведет к искажению интерференционной картины). Кроме того, рассчитывая интерференционные картины в различных опытах, можно довольно точно определять длину волны света, показатель преломления среды, радиус кривизны линзы и многие другие параметры. В технике также широко применяют оптические измерительные приборы, основанные на явлении интерференции – интерферометры.
Рис. 3.10 Остановимся кратко на одном из практических применений интерференции – просветлении оптики. Современные оптические приборы содержат много различных линз, проходя через которые, свет испытывает многократное отражение, вследствие чего ослабляется интенсивность прошедшего света. А это, в свою очередь, приводит к уменьшению эффективности использования оптического прибора. Кроме того, вышеупомянутое многократное отражение света приводит к возникновению бликов. Чтобы устранить эти недостатки на поверхности линз наносят тонкие «просветляющие» пленки, показатель n пл преломления которых, меньше, чем показатель n л преломления линз (рис. 3.10). Кроме того эти пленки имеют малый коэффициент отражения. Толщина «просветляющей» пленки подбирается так, чтобы при интерференции световых волн 1 и 2 (см. рис. 3.10), отраженных от поверхностей пленки и линзы, они гасили друг друга. Рассмотрим нормальное падение света на поверхность пленки. Так как отражение волн 1 и 2 происходит от оптически более плотных сред, то их оптическую разность хода можно записать, как где n – показатель преломления пленки. Поскольку на объективы фотоаппаратов падает белый свет, то невозможно с помощью просветляющей пленки добиться одновременного гашения всех длин волн, составляющих его. Толщину пленки подбирают так, чтобы она гасила лучи с l0 = 555 нм (зеленый цвет), к которым наиболее всего восприимчив глаз человека. «Просветленные» таким образом объективы фотоаппаратов кажутся в белом свете голубовато–красными. Вопросы и задания для самоконтроля к лекции 9 1. 2. Световая волна падает на стеклянную пластинку с показателем преломления n из воздуха (см. рис.). Используя обозначения указанные на рисунке, запишите оптическую разность хода лучей выходящих из пластинки. 3. Тонкую пленку освещают белым светом. Вследствие явления интерференции в отраженном свете наблюдается зеленый цвет. Каким будет ее цвет при уменьшении толщины 4. Монохроматический пучок света (l = 600 нм) падает по нормали на стеклянный клин с углом 5. Объясните явление просветление оптических стекол. На поверхность объектива (n об = 1,5) нанесена тонкая пленка (n пл < n об) толщиной 110 нм, на которую нормально падает монохроматический свет (l = 600 нм). Найдите значение n пл показателя преломления пленки, при котором она будет «просветляющей» для света указанной длины волны.
Лекция 10 Основные понятия и законы, которые должны быть освоены в ходе лекции: дифракция, принцип Гюйгенса – Френеля, зоны Френеля и их свойства; расчет амплитуды и интенсивности световой волны в точке наблюдения; дифракция Френеля на отверстии и на диске; зонные пластинки. Дифракция Дифракция света – комплекс явлений, наблюдаемых при распространении световой волны в среде с резкими оптическими неоднородностями и связанных с нарушением законов геометрической оптики: в результате дифракции свет отклоняется от прямолинейного распространения и, огибая препятствия, оказывается в области геометрической тени. При этом наблюдается пространственное перераспределение интенсивности световой волны – интерференция. Для наблюдения дифракции необходимо, чтобы размеры оптических неоднородностей (преград, экранов, щелей) были соизмеримы с длиной световой волны. Для объяснения дифракции используют принцип Гюйгенса – Френеля (сформулирован в 1815 г.), в соответствии с которым каждая точка волнового фронта является источником вторичных волн, когерентных между собой. Огибающая этих волн определяет положение волнового фронта в следующий момент времени. В случае распространения света в однородной изотропной среде, вторичные когерентные волны являются сферическими. Вторичные когерентные волны, накладываясь друг на друга, интерферируют между собой. Учитывая амплитуды и фазы вторичных волн, можно рассчитать амплитуду результирующей волны в любой точке пространства. В качестве примера объяснения дифракции на основе принципа Гюйгенса – Френеля, рассмотрим преграду с узкой щелью, на которую падает плоская волна (рис. 3.11).
Рис. 3.11 В момент времени Метод зон Френеля Рассмотрим точечный источник света S, от которого в однородной среде распространяется сферическая волна, возбуждающая в точке P световое колебание (рис. 3.12).
Рис. 3.12 Для нахождения амплитуды световой волны в точке P воспользуемся принципом Гюйгенса – Френеля. Пусть a = 0 S – расстояние от точечного источника S света до волнового фронта, а b = 0 P – расстояние от фронта волны до точки наблюдения P. Френель разбил волновой фронт на кольцевые зоны – зоны Френеля, построенные так, что расстояния от краев соседних зон до точки наблюдения P отличаются на
Рис. 3.13 Выражая радиус rm произвольной зоны Френеля с номером m, с помощью теоремы Пифагора из D SAB и D ABP, и учитывая, что высота сферического сегмента h мала (см. рис. 3.13) получим: Если волна плоская (источник света удален на бесконечность: Расчеты показывают, что на полностью открытом волновом фронте укладывается огромное количество зон Френеля, причем площади всех зон примерно одинаковы. Однако, с увеличением номера зоны Френеля, уменьшается ее угловой размер (угол, под которым эта зона видна из точки наблюдения) и увеличивается расстояние от нее до точки наблюдения P. Все это приводит к тому, что с увеличением номера зоны амплитуда А m колебания, возбуждаемого вторичной волной, приходящей от зоны Френеля с номером m, в точке P уменьшается. Таким образом, для амплитуд колебаний, возбуждаемых в точке P наблюдения зонами Френеля, справедливы неравенства
Кроме того амплитуда световой волны, приходящей в точку наблюдения от зоны с номером m может быть выражена в виде
Учтем, что согласно построению зон Френеля, волны, приходящие в точку наблюдения P от соседних зон, имеют оптическую разность хода
При полностью открытом волновом фронте Таким образом, при полностью открытом волновом фронте, амплитуда световой волны в точке P равна половине амплитуды, создаваемой только лишь одной первой (центральной) зоной Френеля Если на пути световой волны поместить непрозрачный экран с отверстием, открывающим только одну первую зону Френеля, то амплитуда световых колебаний в точке P будет равна A 1, т. е. в два раза больше, а интенсивность света ( Дифракция Френеля на диске. Пусть на пути сферической волны, распространяющейся от точечного источника света S, расположена преграда в виде диска, перекрывающая m зон Френеля (рис. 3.14, а). Тогда амплитуда результирующей световой волны в точке P равна следовательно, в точке P всегда наблюдается светлое пятно – интерференционный максимум, соответствующий половине действия первой открытой зоны Френеля (зоны с номером m +1).
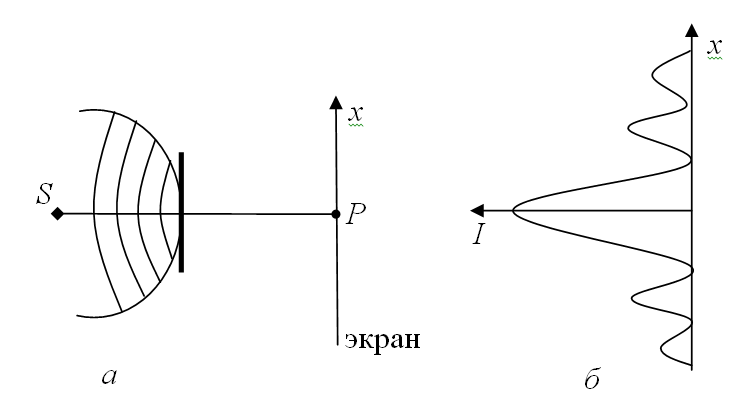
Рис. 3.14 Наблюдаемый на экране центральный максимум, окружен концентрическими темными и светлыми кольцами, возникающими на границе геометрической тени. Распределение интенсивности I света на экране в этом случае изображено на рис. 3.14, б. В случае, если преграда перекрывает много зон Френеля (m – велико),
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.57.41 (0.012 с.) |


 . Приравнивая оптическую разность хода к условию минимума, находим минимальную толщину пленки (при m = 0), при которой отраженные от пленки световые волны гасят друг друга
. Приравнивая оптическую разность хода к условию минимума, находим минимальную толщину пленки (при m = 0), при которой отраженные от пленки световые волны гасят друг друга , (3.17)
, (3.17)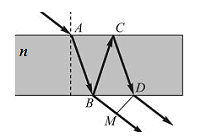 Сформулируйте определение полос равной толщины и равного наклона.
Сформулируйте определение полос равной толщины и равного наклона. при его вершине. Рассчитайте количество светлых интерференционных полос, приходящихся на 1 см длины клина и наблюдаемых в отраженном свете.
при его вершине. Рассчитайте количество светлых интерференционных полос, приходящихся на 1 см длины клина и наблюдаемых в отраженном свете.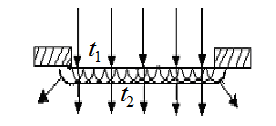
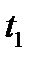 фронт волны находится в этой щели и его каждая точка является источником вторичных когерентных сферических волн, проходящих за время dt расстояние
фронт волны находится в этой щели и его каждая точка является источником вторичных когерентных сферических волн, проходящих за время dt расстояние 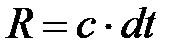 . Положение фронта волны в момент времени
. Положение фронта волны в момент времени 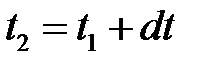 находится, как огибающая фронтов вторичных волн. Поскольку скорость волны в каждой точке волнового фронта перпендикулярна к нему, то имеются участки фронта волны, обеспечивающие проникновение света в область геометрической тени (см. рис. 3.11). Если размеры этих участков фронта волны соизмеримы с размерами щели, то дифракция света будет наблюдаться. Если же они существенно меньше размеров щели, то свет будет проходить через щель в соответствии с законами геометрической оптики, а явление дифракции будет не заметно [5].
находится, как огибающая фронтов вторичных волн. Поскольку скорость волны в каждой точке волнового фронта перпендикулярна к нему, то имеются участки фронта волны, обеспечивающие проникновение света в область геометрической тени (см. рис. 3.11). Если размеры этих участков фронта волны соизмеримы с размерами щели, то дифракция света будет наблюдаться. Если же они существенно меньше размеров щели, то свет будет проходить через щель в соответствии с законами геометрической оптики, а явление дифракции будет не заметно [5].
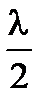 (l – длина световой волны в той среде, в которой распространяется волна).
(l – длина световой волны в той среде, в которой распространяется волна).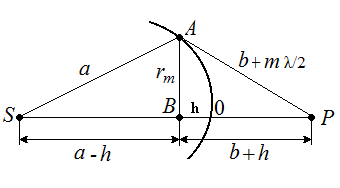
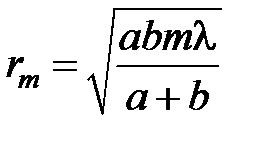 . (3.18)
. (3.18)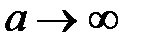 ), то радиус rm зоны Френеля с номером m может быть выражен:
), то радиус rm зоны Френеля с номером m может быть выражен: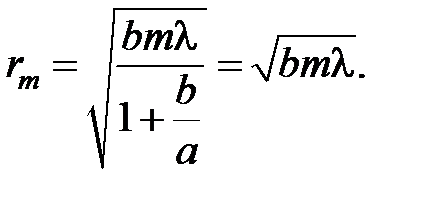 (3.19)
(3.19)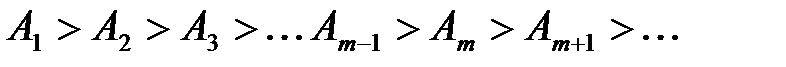
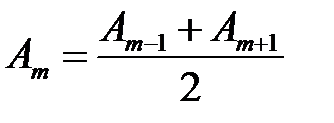 .
.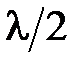 (что соответствует разности фаз, равной π) и, в соответствии с условием интерференционного минимума, ослабляют друг друга. Поэтому амплитуду результирующей световой волны в точке P можно найти в виде:
(что соответствует разности фаз, равной π) и, в соответствии с условием интерференционного минимума, ослабляют друг друга. Поэтому амплитуду результирующей световой волны в точке P можно найти в виде: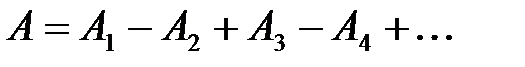 , или
, или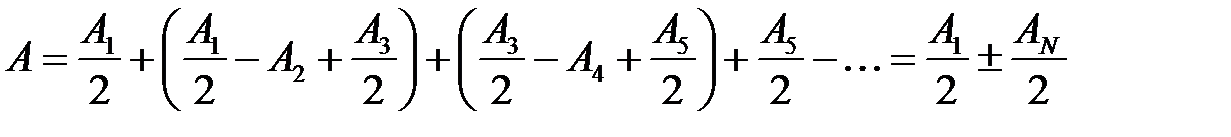
 , поэтому вклад зоны Френеля с номером N пренебрежимо мал по сравнению с вкладом от первой зоны Френеля (
, поэтому вклад зоны Френеля с номером N пренебрежимо мал по сравнению с вкладом от первой зоны Френеля (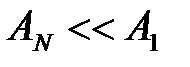 ).
). . (3.20)
. (3.20)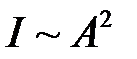 ) – в четыре раза больше, чем при отсутствии экрана.
) – в четыре раза больше, чем при отсутствии экрана.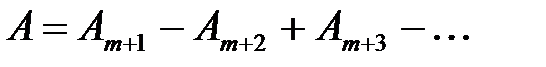
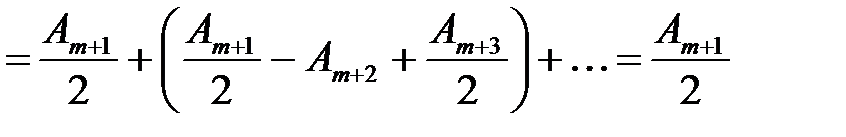 ,
,
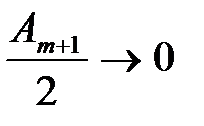 и
и  . Если диск закрывает лишь часть центральной (первой) зоны Френеля, то интенсивность света I на экране остается практически одинаковой во всех точках.
. Если диск закрывает лишь часть центральной (первой) зоны Френеля, то интенсивность света I на экране остается практически одинаковой во всех точках.


