
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Явление электромагнитной индукцииСодержание книги
Поиск на нашем сайте
ОГЛАВЛЕНИЕ Электромагнитные явления. 7 Лекция 1. 7 1.1. Явление электромагнитной индукции. 7 1.1.1 Опыты Фарадея. 7 1.1.2. Закон электромагнитной индукции Фарадея. 8 1.1.3. Природа сторонних сил. 8 1.1.4. Правило Ленца. 10 1.1.5. Токи Фуко. 11 Вопросы и задания для самоконтроля к лекции 1. 12 Лекция 2. 13 1.2. Явление самоиндукции. 13 1.2.1. Индуктивность контура. Индуктивность соленоида. 13 1.2.2. ЭДС самоиндукции. Правило Ленца. 14 1.2.3. Зависимость силы тока от времени при размыкании и замыкании цепи 15 1.2.4. Энергия магнитного поля контура с током. Объемная плотность энергии магнитного поля. 16 Вопросы и задания для самоконтроля к лекции 2. 17 Колебания и волны.. 19 Лекция 3. 19 2.1. Классификация колебаний. 19 2.2. Незатухающие механические колебания. 20 2.2.1.Условия возникновения колебаний. 20 2.2.2. Уравнение незатухающих гармонических колебаний. Основные характеристики незатухающих колебаний. 21 2.3. Затухающие колебания. 24 2.3.1. Уравнение затухающих колебаний. 24 2.3.2. Основные характеристики затухающих колебаний. 26 2.4. Вынужденные механические колебания. 27 2.4.1. Уравнение вынужденных механических колебаний. 27 2.4.2. Механический резонанс. 28 Вопросы и задания для самоконтроля к лекции 3. 29 Лекция 4. 31 2.5. Сложение гармонических колебаний. 31 2.5.1. Диаграмма вектора амплитуды. Сложение гармонических колебаний одного направления и одинаковой частоты.. 31 2.5.2. Биения. 33 2.5.3. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу 35 Вопросы и задания для самоконтроля к лекции 4. 37 Лекция 5. 38 2.6. Свободные незатухающие электромагнитные колебания. 38 2.6.1. Условия возникновения колебаний. 38 2.6.2. Уравнения незатухающих электромагнитных колебаний. 39 2.7. Затухающие электромагнитные колебания 2.7.1. Уравнение затухающих электромагнитных колебаний. 41 2.7.2. Характеристики затухающих электромагнитных колебаний. 43 Вопросы и задания для самоконтроля к лекции 5. 45 Лекция 6. 46 2.8. Волны в упругой среде. 46 2.8.1. Основные характеристики волн. 47 2.8.2. Уравнение плоской механической волны. 48 2.8.3. Волновое уравнение. 49 Вопросы и задания для самоконтроля к лекции 6. 50 Лекция 7. 51 2.9. Электромагнитные волны.. 51 2.9.1. Основные свойства электромагнитных волн. Волновое уравнение 51 2.9.2. Объемная плотность энергии ЭМВ. Поток энергии. Вектор Умова – Пойнтинга. 55
Вопросы и задания для самоконтроля к лекции 7. 56 Волновая оптика. 57 Лекция 8. 57 3.1. Понятие световая волна и световой вектор. 57 3.2. Интерференция света. 57 3.2.1. Оптическая длина пути и оптическая разность хода. Условия максимума и минимума интенсивности света. 59 3.2.2. Расчет интерференционной картины от двух когерентных источников света (опыт Юнга) 61 Вопросы и задания для самоконтроля к лекции 8. 63 Лекция 9. 64 3.2.3. Интерференция в тонких пленках. 64 3.2.4. Полосы равной толщины (клин, кольца Ньютона) и полосы равного наклона. 66 3.2.5. Практическое применение интерференции света. 69 Вопросы и задания для самоконтроля к лекции 9. 71 Лекция 10. 72 3.3. Дифракция. 72 3.3.1. Метод зон Френеля. 73 3.3.2. Дифракция Френеля на диске. 76 3.3.4. Амплитудная и фазовая зонные пластинки. 78 Вопросы и задания для самоконтроля к лекции 10. 79 Лекция 11. 80 3.3.5. Дифракция в параллельных лучах на одной щели. 80 3.3.6 Дифракция на дифракционной решетке. 82 Вопросы и задания для самоконтроля к лекции 11. 85 Квантовая оптика. 86 Лекция 12. 86 4.1. Тепловое излучение. 86 4.1.1. Характеристики, вводимые для описания теплового 4.1.3. Экспериментальные законы теплового излучения а.ч.т. 89 4.1.4. Объяснение закономерностей теплового излучения а.ч.т. 91 Вопросы и задания для самоконтроля к лекции 12. 94 Лекция 13. 95 4.2. Внешний фотоэффект. 95 4.2.1. Вольт-амперная характеристика, ее основные 4.2.2. Уравнение Эйнштейна для фотоэффекта. 97 4.2.4. Зависимость задерживающего напряжения от частоты. 100 4.3. Эффект Комптона. 101 4.4. Природа электромагнитного излучения. Корпускулярно-волновой дуализм 103 Вопросы и задания для самоконтроля к лекции 13. 104 Элементы квантовой механики. 106 Лекция 14. 106 5.1. Гипотеза де Бройля. Опыты, подтверждающие волновые свойства микрочастиц. 106 5.2. Соотношения неопределенностей Гейзенберга. 109 5.2.1. Соотношения неопределенностей как проявление волновых свойств 109 5.2.2. Условия применимости классической механики для описания движения микрочастиц. 111 5.3. Волновая функция. Стандартные условия. 113 Вопросы и задания для самоконтроля к лекции 14. 114 Лекция 15. 115 5.4. Уравнение Шредингера. 115 5.4.1. Микрочастица в бесконечно глубокой прямоугольной потенциальной яме. 116
5.4.2. Туннельный эффект. 120 Вопросы и задания для самоконтроля к лекции 15. 123 Основы физики атомного ядра. 124 Лекция 16. 124 6.1. Строение и состав атомного ядра. 124 6.1.1.Характеристики атомного ядра. 124 6.1.2. Ядерные силы. Свойства ядерных сил. 125 6.2. Ядерные реакции. 128 6.3. Явление радиоактивности. 129 6.3.1. Виды радиоактивного распада ядер. 129 6.3.2. Основной закон радиоактивного распада. Активность радиоактивного вещества. 130 Вопросы и задания для самоконтроля к лекции 16. 132 Библиографический список. 133 Электромагнитные явления Лекция 1 Основные понятия и законы, которые должны быть освоены в ходе лекции: электромагнитная индукция, ЭДС индукции, закон Фарадея, сила индукционного тока, правило Ленца, вихревое электрическое поле. Опыты Фарадея В 1831 году Майкл Фарадей экспериментально обнаружил, возникновение электрического тока в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего данный контур. Это явление получило название электромагнитной индукции, а возникающий в этом явлении электрический ток – индукционного тока. В опытах Фарадея магнитный поток, пронизывающий первый контур (катушку 1), изменялся различными способами (рис. 1.1): 1) замыкалась и размыкалась цепь второго контура; 2) с помощью реостата изменялась сила тока во втором контуре; 3) второй контур приближался или удалялся относительно первого контура; 4) постоянный магнит приближался или удалялся относительно первого контура [1].
Рис. 1.1 Появление индукционного тока Ii в вышеперечисленных опытах свидетельствует о том, что при изменении магнитного потока сквозь контур, в последнем возникает ЭДС индукции ei. Причем индукционный ток изменял свое направление при смене направления движения магнита, направления движения контуров 1 и 2, при замене нарастающего тока в контуре 2 убывающим со временем током, при замене замыкания цепи второго контура ее размыканием [1]. Кроме того, было экспериментально доказано, что сила индукционного тока Ii и ЭДС индукции ei зависят от скорости изменения магнитного потока, пронизывающего проводящий контур, и не зависят от способа изменения магнитного потока F [1]. Природа сторонних сил Появление ЭДС индукции e i свидетельствует о том, что в проводящем контуре возникают сторонние силы, совершающие работу по разделению разноименных электрических зарядов. Природа сторонних сил различна и зависит от того, в какой ситуации они появляются. Случай 1. В постоянном магнитном поле находится контур переменной площади или вращается контур постоянной площади, или двигается проводник. В этом случае, возникновение ЭДС индукции eiсвязано с действием на свободные заряды силы Лоренца. На рис. 1.2, а, показано, что при движении проводника со скоростью
Рис. 1.2 Случай 2. Неподвижный контур постоянной площади находится в переменном магнитном поле. В этом случае на свободные заряды в проводнике сила Лоренца не действует, и для объяснения возникновения ЭДС индукции e i Максвелл сформулировал следующий постулат: переменное во времени магнитное поле порождает в окружающем пространстве вихревое электрическое поле.
Этот постулат является первым положением теории электромагнитного поля Максвелла. Согласно Максвеллу, линии вихревого электрического поля являются замкнутыми, они связаны с направлением вектора где Правило Ленца Направление индукционного тока можно найти по правилу Ленца: индукционный ток в контуре возникает такого направления, чтобы создаваемое им магнитное поле препятствовало любым изменениям магнитного потока, вызвавшего этот индукционный ток [1]. С правилом Ленца связан знак минус в формуле (1.1). Действительно, если магнитный поток F через плоскость контура возрастает, то тогда Алгоритм применения правила Ленца: 1. Определить в центре проводящего контура направление внешнего магнитного поля 2. Определить увеличивается или уменьшается магнитный поток сквозь контур. 3. Если магнитный поток увеличивается, то направление магнитного поля 4. Зная направление вектора На рис. 1.3 приведен пример определения направления индукционного тока I i с помощью правила Ленца. Пусть проводящий контур находится в возрастающем со временем
Рис. 1.3 Токи Фуко Токи Фуко – это индукционные токи, возникающие в массивных проводниках. Для таких проводников сопротивление R будет мало и поэтому индукционные токи (Ii =e i / R) достигают большой величины. Токи Фуко используются для нагревания и плавления металлических заготовок, получения особо чистых сплавов и соединений металлов. Для этого металлическую заготовку помещают в индукционную печь (соленоид, по которому пропускают переменный ток) [1]. При этом внутри металла возникают индукционные токи, разогревающие металл (вплоть до его плавления). Если в печи создать вакуум и применить левитационный нагрев (в этом случае силы электромагнитного поля не только разогревают металл, но и удерживают его в подвешенном состоянии вне контакта с поверхностью камеры), то получаются особо чистые металлы и сплавы [1]. Кроме того, токи Фуко могут приводить и к негативным эффектам – нагреву сердечников трансформаторов, электродвигателей и т. д. Чтобы уменьшить нежелательное воздействие токов Фуко, массивный проводник набирают в виде отдельных пластин. Сила индукционных токов в отдельных пластинах существенно меньше силы тока, текущего по целому массивному проводнику, поэтому в соответствии с законом Джоуля – Ленца ( Вопросы и задания для самоконтроля к лекции 1 1. Что называют явлением электромагнитной индукции? 2. Плоская проводящая рамка находится в магнитном поле (см. рис.). В каких случаях в рамке возникает ЭДС индукции? 3. 4. Используя закон Фарадея и определение силы тока, выведите формулу 5. Неподвижный проводящий контур находится в изменяющемся со временем магнитном поле. Что является причиной возникновения ЭДС индукции в контуре в этом случае? Лекция 2 Основные понятия и законы, которые должны быть освоены в ходе лекции: магнитный поток самоиндукции, индуктивность контура, ЭДС самоиндукции, ток самоиндукции, правило Ленца, силы тока при размыкании и замыкании цепи, энергия магнитного поля контура с током, объемная плотность энергии магнитного поля. Явление самоиндукции Колебания и волны Лекция 3 Основные понятия и законы, которые должны быть освоены в ходе лекции: гармонические колебания; квазиупругая сила; незатухающие и затухающие колебания; амплитуда, частота, циклическая частота, период и фаза колебаний; законы изменения смещения, скорости, ускорения, кинетической, потенциальной и полной энергии тела, совершающего незатухающие (затухающие) колебания и графики, выражающие эти законы; логарифмический декремент затухания, время релаксации, добротность системы, механический резонанс. Классификация колебаний
Колебания – это процессы, характеризующиеся определенной степенью повторяемости во времени. В зависимости от характера воздействия на колеблющуюся систему внешних сил различают свободные и вынужденные колебания. Свободные колебания совершаются в системе, предоставленной самой себе после однократного выведения ее из положения равновесия (например, качели). Свободные колебания могут быть незатухающими (в отсутствии трения или сопротивления среды) и затухающими. Вынужденные колебания обусловлены внешним периодическим воздействием (например, колебания иглы швейной машины). Колебания называют периодическими, если значения описывающих их величин повторяются через одинаковый промежуток времени, называемый периодом Т. Одними из самых распространенных периодических колебаний являются гармонические колебания – колебания, при которых описывающие их величины изменяются по закону косинуса (синуса). В дальнейшем будем рассматривать только гармонические колебания. Затухающие колебания Механический резонанс Механический резонанс – это явление резкого возрастания амплитуды вынужденных колебаний [3] при приближении частоты вынуждающей силы к некоторой характерной для данной системы частоте Резонансную частоту
откуда получаем выражение Амплитуда колебаний при резонансе равна: В случае если
Рис. 2.7 Зависимость амплитуды колебаний от частоты вынуждающей силы называется резонансной кривой. На рис. 2.7 представлены резонансные кривые для различных значений коэффициента затухания Вопросы и задания для самоконтроля к лекции 3 1. Что называют квазиупругой силой? Чему равен коэффициент квазиупругой силы в случае математического маятника? 2. Четыре системы с одинаковыми массами m и различными коэффициентами упругости k, совершают гармонические колебания в соответствие с нижеприведенными уравнениями. Для какой системы коэффициент упругости наименьший? 1)x = 6sin(3πt+π), см. 4)x = 5cos(5πt+π/2), см. 2)x = 3cos(2πt+π), см. 8)x = 2sin(4πt+π/2), см. 3. Что называют логарифмическим декрементом затухания? 4. Материальная точка совершает затухающие колебания в соответствие с законом 5. Амплитуда затухающих колебаний математического маятника за 1 минуту уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время 4 минуты? 6. Сформулируйте определение механического резонанса. Приведите встречающиеся примеры проявления механического резонанса. Лекция 4 Основные понятия и законы, которые должны быть освоены в ходе лекции: векторная диаграмма, биения, фигуры Лиссажу. Биения Биения − это колебания, с периодически изменяющейся амплитудой, получающиеся в результате сложения двух гармонических колебаний одного направления с близкими частотами. Сами биения не являются гармоническими колебаниями. Выведем уравнение биений. Для этого рассмотрим два гармонических колебания х 1 и х 2, происходящих в одном направлении с близкими частотами (
Тогда результирующее колебание будет происходить по закону где при выводе формулы (2.37) была учтена формула сложения косинусов ( Первый сомножитель в выражении (2.37) изменяется со временем значительно медленнее второго ( Под периодом где На рис. 2.10 приведены графики зависимости амплитуды биений
Рис. 2.10 В общем случае, когда складываются колебания близких частот, но не равных амплитуд, амплитуда результирующего колебания (биений) изменяется в пределах, заключенных в интервале от Приведем пример биений: источником двух звуковых сигналов является звуковой генератор. Сначала генерируются сигналы разных частот, таких, что человек различает эти сигналы как отдельные. По мере сближения с помощью звукового генератора частот этих сигналов, человек начинает вместо двух разных сигналов слышать один, но с переменной амплитудой (биения). При выравнивании частот сигналов человек слышит один звуковой сигнал с постоянной амплитудой. Биения можно использовать, например: 1) для настройки музыкальных инструментов, при анализе восприятия звуков человеком; 2) для определения частоты какого-либо гармонического электрического колебания. Для этого на вход осциллографа подают гармонические колебания от звукового генератора (частоту Лекция 5 Основные понятия и законы, которые должны быть освоены в ходе лекции: электромагнитные колебания (незатухающие и затухающие); колебательный контур; зависимости от времени величин, описывающих электромагнитные колебания и их графики; коэффициент затухания, логарифмический декремент затухания, время релаксации, критическое сопротивление, апериодический режим. Лекция 6 Основные понятия и законы, которые должны быть освоены в ходе лекции: волна; бегущие и стоячие волны; поперечные и продольные волны; волновая поверхность, фронт волны; фазовая скорость, период и длина волны; волновой вектор, волновое число; уравнение плоской механической волны, волновое уравнение. Волны в упругой среде Процесс распространения колебаний в пространстве с течением времени называется волной. Частицы среды, в которой распространяются колебания, волной не увлекаются, а лишь колеблются вблизи своих положений равновесия. Однако энергия колебаний переносится от источника к точкам среды. Волны, переносящие в направлении своего распространения энергию колебательного движения, называются бегущими. Механические волны могут распространяться только в упругих средах, между частицами которых действуют упругие силы. Смещение от положения равновесия какой-то одной частицы в упругой среде приводит к смещению соседней с ней частицы и т. д. – в среде распространяется упругая волна. Различают поперечные и продольные механические волны. Если частицы среды колеблются в направлении, перпендикулярном направлению распространения волны (рис. 2.18, а), то такие волны называются поперечными (например, волна на поверхности жидкости). Если же частицы среды колеблются в направлении распространения волны (рис.18, б), то такие волны называются продольными (например, звук).
Рис. 2.18 Поперечные волны распространяются только в тех средах, в которых возможна деформация сдвига (т. е. в твердых телах и на поверхности жидкостей). Продольные волны распространяются и в твердых телах, и в газах, и в жидкостях, т. е. в средах, в которых возможна деформация сжатия и растяжения. Волновое уравнение Уравнения (2.71), (2.72) плоской волны, распространяющейся в положительном (отрицательном) направлении оси Ох являются решениями дифференциального уравнения второго порядка, называемого волновым: Если плоская гармоническая волна распространяется в произвольном направлении, которое можно задать радиус-вектором Вопросы и задания для самоконтроля к лекции 6 1. Сформулируйте определения поперечной и продольной волны. В каких средах они могут распространяться? 2. Выберите утверждения, которые Вы считаете верными для волны, распространяющейся в упругой среде? 1) фронт волны является волновой поверхностью; 2) волновые поверхности при распространении волны перемещаются; 3) частицы среды вместе с волной не перемещаются, перемещается только фронт волны; 4) волновых поверхностей может быть бесконечное множество. 3. Для двух точек плоской гармонической волны, расстояние между которыми l =3l/4, разность фаз колебаний равна… 1) Dj=4π/3 2) Dj=3π/2 3) Dj=π/2 4) Dj=π 4. Чему равна длина волны с частотой 4 Гц, распространяющейся по шнуру со скоростью 8 м/с? 5. Лекция 7 Основные понятия и законы, которые должны быть освоены в ходе лекции: определение электромагнитной волны (ЭМВ, основные свойства ЭМВ; волновое уравнение; объемная плотность энергии электромагнитной волны; поток энергии; вектор Умова – Пойнтинга. Электромагнитные волны Волновая оптика Лекция 8 Основные понятия и законы, которые должны быть освоены в ходе лекции: световая волна и световой вектор; когерентность и монохроматичность волн; интерференция света и условия ее наблюдения; Оптическая длина пути и оптическая разность хода волн; условия максимума и минимума интенсивности света. Интерференция света Интерференция света – это такое наложение световых волн, при котором наблюдается пространственное перераспределение интенсивности результирующей волны: в одних точках пространства, накладываемые световые волны усиливают друг друга (светлые области), а в других – ослабляют (темные области). Не все световые волны могут интерферировать между собой. Интерференция наблюдается только при наложении когерентных световых волн. Волны являются когерентными, если их частоты одинаковы, а разность фаз с течением времени не изменяется. Кроме того для наблюдения интерференционной картины необходимо, чтобы колебания световых векторов Любые два независимых источника света излучают некогерентные световые волны. Чтобы получить когерентные волны, необходимо каким-либо образом разделить свет от одного источника на две части примерно одинаковой интенсивности. Рассмотрим некоторые способы получения когерентных световых волн. 1. Щели Юнга Две узкие (десятые доли мм) параллельные друг другу щели S 1 и S 2, вырезанные в непрозрачном экране, освещаются светом, прошедшим через столь же узкую щель S, равноотстоящую от S 1 и S 2 (рис. 3.1). Щели S 1 и S 2 являются источниками вторичных когерентных волн. Накладываясь друг на друга в точке А на экране Э, волны интерферируют.
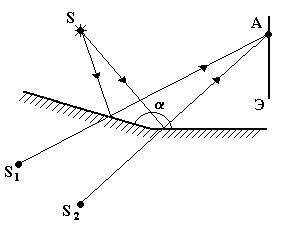
Рис. 3.1 2. Зеркала Френеля Как видно из рис. 3.2, световая волна одновременно падает на два зеркала, расположенных под углом a » 1800. Отраженные от зеркал лучи интерферируют на экране в точке А. Когерентные части волны распространяются так, как будто бы они испускаются двумя разными источниками S 1 и S 2.
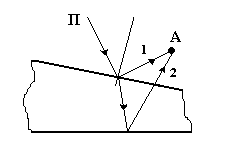
Рис. 3.2 3. Тонкая прозрачная пленка При отражении падающего светового луча П от нижней и верхней поверхностей пленки, возникают когерентные волны 1 и 2 (рис. 3.3), которые при наложении будут интерферировать.
Рис. 3.3 Лекция 9 Основные понятия и законы, которые должны быть освоены в ходе лекции: интерференция в тонких пленках; полосы равной толщины; кольца Ньютона; полосы равного наклона; просветление оптики. Лекция 10 Основные понятия и законы, которые должны быть освоены в ходе лекции: дифракция, принцип Гюйгенса – Френеля, зоны Френеля и их свойства; расчет амплитуды и интенсивности световой волны в точке наблюдения; дифракция Френеля на отверстии и на диске; зонные пластинки. Дифракция Дифракция света – комплекс явлений, наблюдаемых при распространении световой волны в среде с резкими оптическими неоднородностями и связанных с нарушением законов геометрической оптики: в результате дифракции свет отклоняется от прямолинейного распространения и, огибая препятствия, оказывается в области геометрической тени. При этом наблюдается пространственное перераспределение интенсивности световой волны – интерференция. Для наблюдения дифракции необходимо, чтобы размеры оптических неоднородностей (преград, экранов, щелей) были соизмеримы с длиной световой волны. Для объяснения дифракции используют принцип Гюйгенса – Френеля (сформулирован в 1815 г.), в соответствии с которым каждая точка волнового фронта является источником вторичных волн, когерентных между собой. Огибающая этих волн определяет положение волнового фронта в следующий момент времени. В случае распространения света в однородной изотропной среде, вторичные когерентные волны являются сферическими. Вторичные когерентные волны, накладываясь друг на друга, интерферируют между собой. Учитывая амплитуды и фазы вторичных волн, можно рассчитать амплитуду результирующей волны в любой точке пространства. В качестве примера объяснения дифракции на основе принципа Гюйгенса – Френеля, рассмотрим преграду с узкой щелью, на которую падает плоская волна (рис. 3.11).
Рис. 3.11 В момент времени Метод зон Френеля Рассмотрим точечный источник света S, от которого в однородной среде распространяется сферическая волна, возбуждающая в точке P световое колебание (рис. 3.12).
Рис. 3.12 Для нахождения амплитуды световой волны в точке P воспользуемся принципом Гюйгенса – Френеля. Пусть a = 0 S – расстояние от точечного источника S света до волнового фронта, а b = 0 P – расстояние от фронта волны до точки наблюдения P. Френель разбил волновой фронт на кольцевые зоны – зоны Френеля, построенные так, что расстояния от краев соседних зон до точки наблюдения P отличаются на
Рис. 3.13 Выражая радиус rm произвольной зоны Френеля с номером m, с помощью теоремы Пифагора из D SAB и D ABP, и учитывая, что высота сферического сегмента h мала (см. рис. 3.13) получим: Если волна плоская (источник света удален на бесконечность: Расчеты показывают, что на полностью открытом волновом фронте укладывается огромное количество зон Френеля, причем площади всех зон примерно одинаковы. Однако, с увеличением номера зоны Френеля, уменьшается ее угловой размер (угол, под которым эта зона видна из точки наблюдения) и увеличивается расстояние от нее до точки наблюдения P. Все это приводит к тому, что с увеличением номера зоны амплитуда А m колебания, возбуждаемого вторичной волной, приходящей от зоны Френеля с номером m, в точке P уменьшается. Таким образом, для амплитуд колебаний, возбуждаемых в точке P наблюдения зонами Френеля, справедливы неравенства
Кроме того амплитуда световой волны, приходящей в точку наблюдения от зоны с номером m может быть выражена в виде
Учтем, что согласно построению зон Френеля, волны, приходящие в точку наблюдения P от соседних зон, имеют оптическую разность хода
При полностью открытом волновом фронте | |||||||
|
| Поделиться: |

 . 41
. 41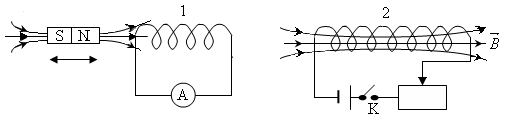
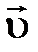 в магнитном поле, электроны под действием силы Лоренца перемещаются к одному концу проводника, вследствие чего, на нем возникает избыток электронов, а на другом конце – их недостаток. Таким образом, сторонней силой, разделяющей заряды, является сила Лоренца.
в магнитном поле, электроны под действием силы Лоренца перемещаются к одному концу проводника, вследствие чего, на нем возникает избыток электронов, а на другом конце – их недостаток. Таким образом, сторонней силой, разделяющей заряды, является сила Лоренца.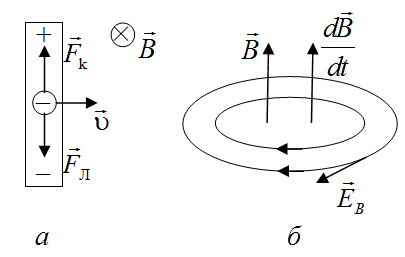
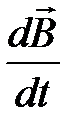 правилом левого буравчика и лежат в плоскости, перпендикулярной к вектору
правилом левого буравчика и лежат в плоскости, перпендикулярной к вектору 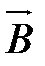 (рис. 1.2, б). Именно силы вихревого электрического поля совершают работу по разделению разноименных зарядов в проводнике, т. е. являются сторонними силами.
(рис. 1.2, б). Именно силы вихревого электрического поля совершают работу по разделению разноименных зарядов в проводнике, т. е. являются сторонними силами.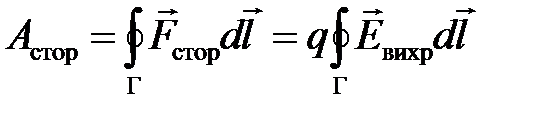 ; (1.3)
; (1.3)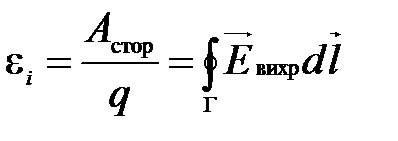 , (1.4)
, (1.4)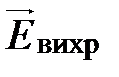 – вектор напряженности электрического поля, а контур (Г) (воображаемая линия) располагается внутри проводника (проводящего контура) [1].
– вектор напряженности электрического поля, а контур (Г) (воображаемая линия) располагается внутри проводника (проводящего контура) [1].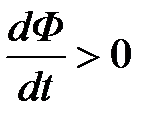 и согласно (1.1) e i <0, т. е. магнитный поток F i, создаваемый индукционным током, будет противоположен по знаку магнитному потоку F. При убывании F
и согласно (1.1) e i <0, т. е. магнитный поток F i, создаваемый индукционным током, будет противоположен по знаку магнитному потоку F. При убывании F 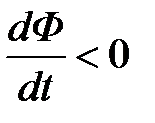 , e i >0 и магнитные потоки F i,и F совпадают по знаку[1].
, e i >0 и магнитные потоки F i,и F совпадают по знаку[1].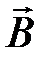 .
. , созданного индукционным током, должно быть противоположно направлению вектора
, созданного индукционным током, должно быть противоположно направлению вектора 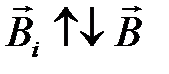 ), если магнитный поток уменьшается, то –
), если магнитный поток уменьшается, то – 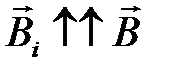 .
.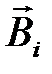 , по правилу Буравчика (правой руки) определить направление индукционного тока I i.
, по правилу Буравчика (правой руки) определить направление индукционного тока I i.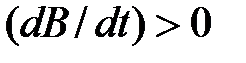 внешнем магнитном поле. Тогда магнитный поток F, пронизывающий контур, тоже увеличивается. Следовательно, силовые линии магнитного поля
внешнем магнитном поле. Тогда магнитный поток F, пронизывающий контур, тоже увеличивается. Следовательно, силовые линии магнитного поля 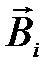 , созданного появившемся индукционным током, направлены противоположно линиям
, созданного появившемся индукционным током, направлены противоположно линиям 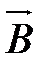 индукции внешнего магнитного поля. Зная направление вектора
индукции внешнего магнитного поля. Зная направление вектора 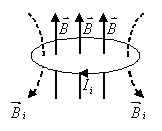
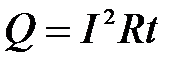 ), уменьшается выделяемое в проводнике количество теплоты.
), уменьшается выделяемое в проводнике количество теплоты.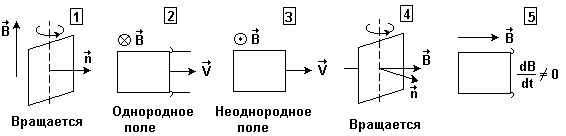
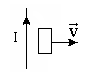 Прямоугольная проводящая рамка удаляется от прямолинейного проводника с током в перпендикулярном к нему направлении, как показано на рисунке. С помощью правила Ленца, определите направление возникающего в рамке индукционного тока.
Прямоугольная проводящая рамка удаляется от прямолинейного проводника с током в перпендикулярном к нему направлении, как показано на рисунке. С помощью правила Ленца, определите направление возникающего в рамке индукционного тока.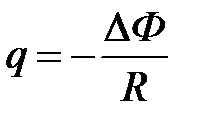 – для заряда, протекшего по замкнутому проводящему контуру за время изменения магнитного потока
– для заряда, протекшего по замкнутому проводящему контуру за время изменения магнитного потока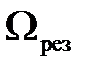 .
.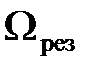 находим как частоту, при которой амплитуда вынужденных колебаний достигает максимального значения (знаменатель выражения (2.29) при этом имеет минимум):
находим как частоту, при которой амплитуда вынужденных колебаний достигает максимального значения (знаменатель выражения (2.29) при этом имеет минимум):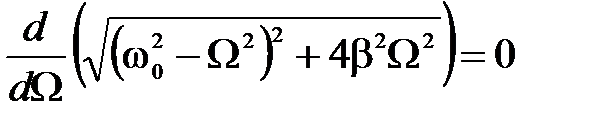 ,
,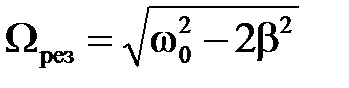 . (2.31)
. (2.31)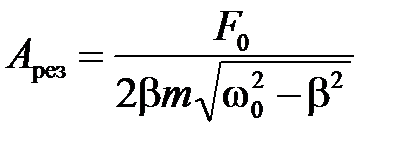 . (2.32)
. (2.32)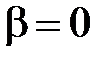 (сопротивление среды отсутствует), из формулы (2.31) следует, что
(сопротивление среды отсутствует), из формулы (2.31) следует, что 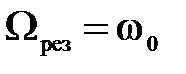 , а амплитуда вынужденных колебаний
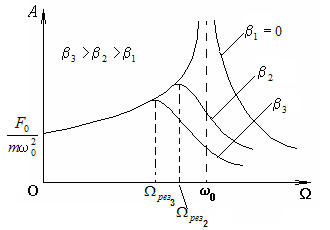
, а амплитуда вынужденных колебаний 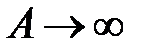 .
.
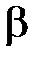 . Высота и ширина резонансного пика, зависят от коэффициента затухания
. Высота и ширина резонансного пика, зависят от коэффициента затухания 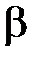 .
.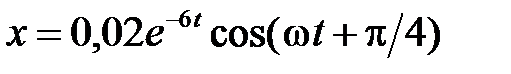 . Логарифмический декремент затухания колебаний λ=0,001. Определите коэффициент затухания b и частоту w затухающих колебаний.
. Логарифмический декремент затухания колебаний λ=0,001. Определите коэффициент затухания b и частоту w затухающих колебаний. >>
>> 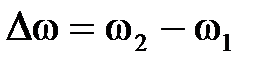 ) и равными амплитудами (для удобства расчетов):
) и равными амплитудами (для удобства расчетов):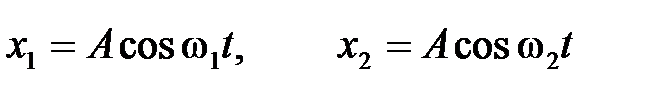 .
.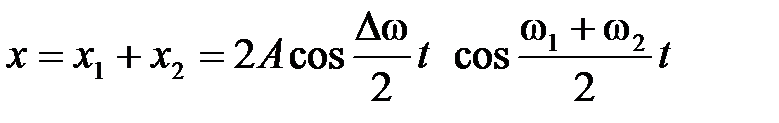 , (2.37)
, (2.37)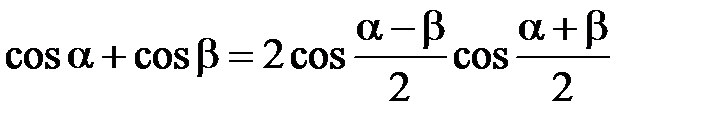 ).
).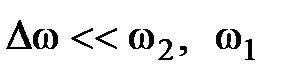 ), поэтому можно считать, что результирующее колебание
), поэтому можно считать, что результирующее колебание 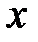 представляет собой колебание с циклической частотой
представляет собой колебание с циклической частотой 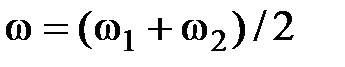 и с изменяющейся со временем амплитудой [3]
и с изменяющейся со временем амплитудой [3]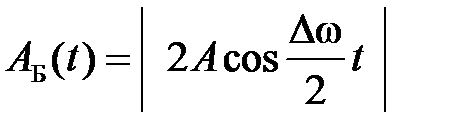 . (2.38)
. (2.38)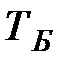 биений – понимают период изменения амплитуды результирующего колебания:
биений – понимают период изменения амплитуды результирующего колебания: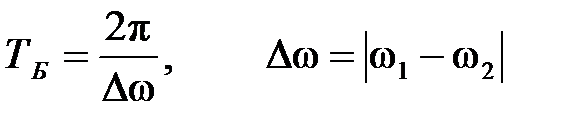 , (2.39)
, (2.39)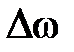 – циклическая частота биений [3].
– циклическая частота биений [3].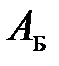 и смещения
и смещения  м.т. от времени t [3].
м.т. от времени t [3].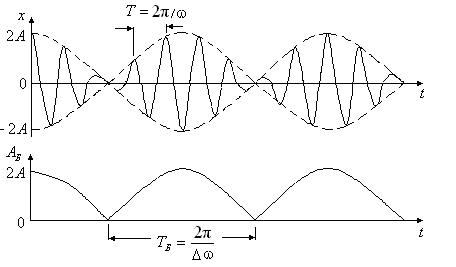
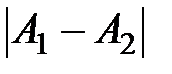 до (
до (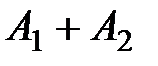 ).
).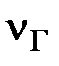 этих колебаний можно изменять) и гармонические колебания с неизвестной частотой
этих колебаний можно изменять) и гармонические колебания с неизвестной частотой 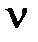 от какого-либо источника. По наблюдаемой на экране осциллографа картине биений определяют период биений
от какого-либо источника. По наблюдаемой на экране осциллографа картине биений определяют период биений 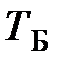 и частоту колебаний (
и частоту колебаний (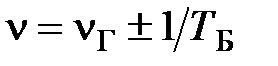 ) [3].
) [3].
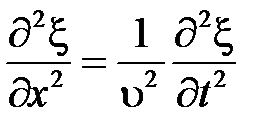 . (2.75)
. (2.75)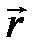 ,то ее волновое уравнение и уравнение волны запишутся, соответственно, следующим образом
,то ее волновое уравнение и уравнение волны запишутся, соответственно, следующим образом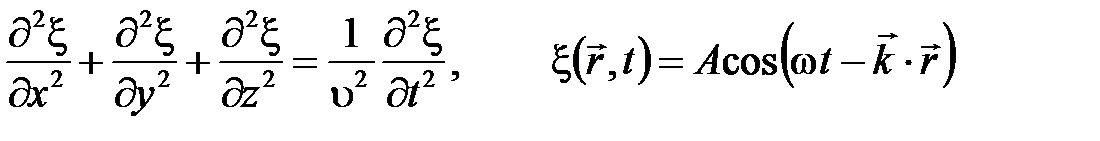 , (2.76)
, (2.76)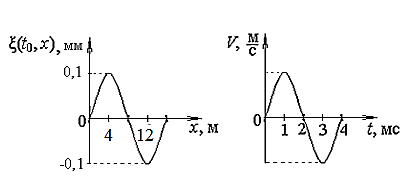 На рисунке приведены фотография плоской волны, распространяющейся в упругой среде вдоль оси 0 х, в некоторый момент времени и зависимость скорости колебаний произвольной частицы среды от времени. Используя приведенные зависимости, определите фазовую скорость волны и максимальную скорость колебаний частиц среды.
На рисунке приведены фотография плоской волны, распространяющейся в упругой среде вдоль оси 0 х, в некоторый момент времени и зависимость скорости колебаний произвольной частицы среды от времени. Используя приведенные зависимости, определите фазовую скорость волны и максимальную скорость колебаний частиц среды.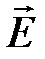 , интерферирующих волн, совершались вдоль одного или близких направлений.
, интерферирующих волн, совершались вдоль одного или близких направлений.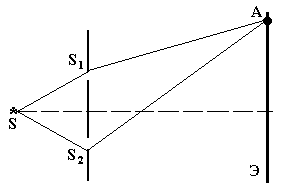
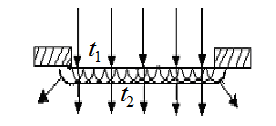
 фронт волны находится в этой щели и его каждая точка является источником вторичных когерентных сферических волн, проходящих за время dt расстояние
фронт волны находится в этой щели и его каждая точка является источником вторичных когерентных сферических волн, проходящих за время dt расстояние 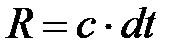 . Положение фронта волны в момент времени
. Положение фронта волны в момент времени 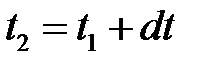 находится, как огибающая фронтов вторичных волн. Поскольку скорость волны в каждой точке волнового фронта перпендикулярна к нему, то имеются участки фронта волны, обеспечивающие проникновение света в область геометрической тени (см. рис. 3.11). Если размеры этих участков фронта волны соизмеримы с размерами щели, то дифракция света будет наблюдаться. Если же они существенно меньше размеров щели, то свет будет проходить через щель в соответствии с законами геометрической оптики, а явление дифракции будет не заметно [5].
находится, как огибающая фронтов вторичных волн. Поскольку скорость волны в каждой точке волнового фронта перпендикулярна к нему, то имеются участки фронта волны, обеспечивающие проникновение света в область геометрической тени (см. рис. 3.11). Если размеры этих участков фронта волны соизмеримы с размерами щели, то дифракция света будет наблюдаться. Если же они существенно меньше размеров щели, то свет будет проходить через щель в соответствии с законами геометрической оптики, а явление дифракции будет не заметно [5].
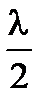 (l – длина световой волны в той среде, в которой распространяется волна).
(l – длина световой волны в той среде, в которой распространяется волна).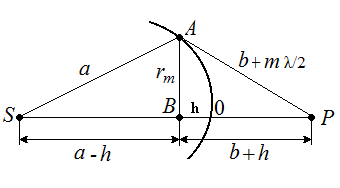
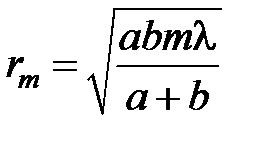 . (3.18)
. (3.18)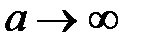 ), то радиус rm зоны Френеля с номером m может быть выражен:
), то радиус rm зоны Френеля с номером m может быть выражен: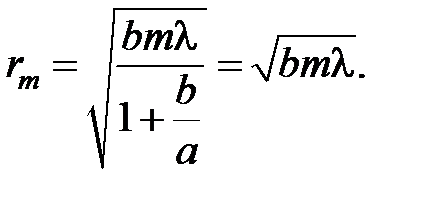 (3.19)
(3.19)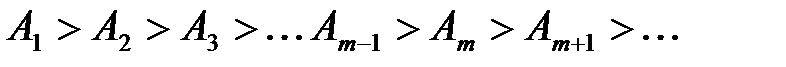
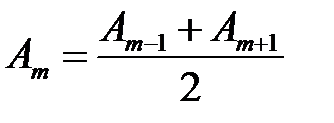 .
.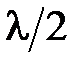 (что соответствует разности фаз, равной π) и, в соответствии с условием интерференционного минимума, ослабляют друг друга. Поэтому амплитуду результирующей световой волны в точке P можно найти в виде:
(что соответствует разности фаз, равной π) и, в соответствии с условием интерференционного минимума, ослабляют друг друга. Поэтому амплитуду результирующей световой волны в точке P можно найти в виде: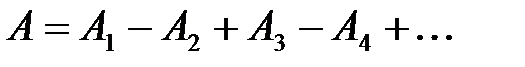 , или
, или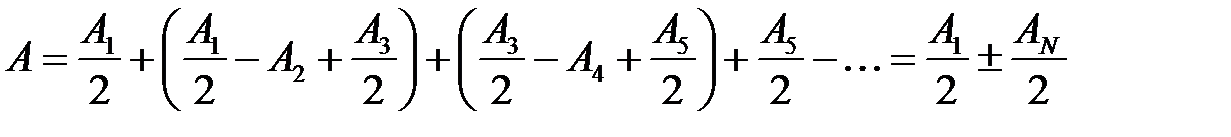
 , поэтому вклад зоны Френеля с номером N пренебрежимо мал по сравнению с вкладом от первой зоны Френеля (
, поэтому вклад зоны Френеля с номером N пренебрежимо мал по сравнению с вкладом от первой зоны Френеля (


