
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение гармонических колебанийСодержание книги
Поиск на нашем сайте
Диаграмма вектора амплитуды. Сложение гармонических колебаний одного направления и одинаковой частоты Гармонические колебания можно представить с помощью вектора амплитуды, вращающегося вокруг точки O с угловой скоростью w (рис. 2.8). Длина этого вектора равна амплитуде колебаний. В начальный момент времени угол между вектором амплитуды и положительным направлением оси x равен начальной фазе колебаний. Тогда проекция вектора
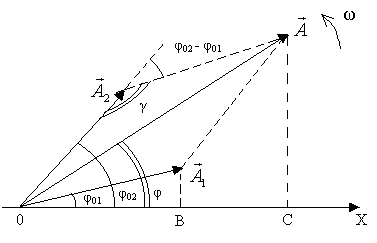
Рис. 2.8 С помощью векторной диаграммы удобно складывать колебания одинаковой частоты и одного направления. Рассмотрим подробнее. Пусть тело одновременно участвует в двух гармонических колебаниях одинаковой частоты, происходящих в одном направлении согласно законам Результирующее движение представляет собой сумму колебаний
Рис. 2.9 Чтобы найти амплитуду и начальную фазу результирующего колебания воспользуемся диаграммой вектора амплитуды. Из точки O проведем вектора Проекции векторов где A – амплитуда, Рассмотрим некоторые частные случаи сложения колебаний. 1. т. е. если разность фаз складываемых колебаний равна четному числу π, то тогда колебания максимально усиливают друг друга. 2. т. е. если разность фаз складываемых колебаний равна нечетному числу π, то тогда колебания максимально ослабляют друг друга [3]. 3. Биения Биения − это колебания, с периодически изменяющейся амплитудой, получающиеся в результате сложения двух гармонических колебаний одного направления с близкими частотами. Сами биения не являются гармоническими колебаниями. Выведем уравнение биений. Для этого рассмотрим два гармонических колебания х 1 и х 2, происходящих в одном направлении с близкими частотами (
Тогда результирующее колебание будет происходить по закону где при выводе формулы (2.37) была учтена формула сложения косинусов ( Первый сомножитель в выражении (2.37) изменяется со временем значительно медленнее второго ( Под периодом где На рис. 2.10 приведены графики зависимости амплитуды биений
Рис. 2.10 В общем случае, когда складываются колебания близких частот, но не равных амплитуд, амплитуда результирующего колебания (биений) изменяется в пределах, заключенных в интервале от Приведем пример биений: источником двух звуковых сигналов является звуковой генератор. Сначала генерируются сигналы разных частот, таких, что человек различает эти сигналы как отдельные. По мере сближения с помощью звукового генератора частот этих сигналов, человек начинает вместо двух разных сигналов слышать один, но с переменной амплитудой (биения). При выравнивании частот сигналов человек слышит один звуковой сигнал с постоянной амплитудой. Биения можно использовать, например: 1) для настройки музыкальных инструментов, при анализе восприятия звуков человеком; 2) для определения частоты какого-либо гармонического электрического колебания. Для этого на вход осциллографа подают гармонические колебания от звукового генератора (частоту
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.115.125 (0.009 с.) |

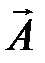 на ось
на ось 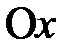 в момент времени t = 0 равна
в момент времени t = 0 равна 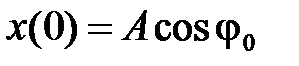 . С течением времени проекция на ось O х вращающегося вектора амплитуды изменяется по гармоническому закону
. С течением времени проекция на ось O х вращающегося вектора амплитуды изменяется по гармоническому закону 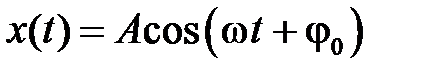 . Такой способ представления гармонических колебаний называют векторной диаграммой или диаграммой вектора амплитуды.
. Такой способ представления гармонических колебаний называют векторной диаграммой или диаграммой вектора амплитуды.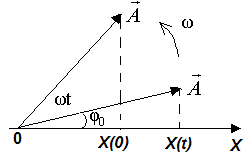
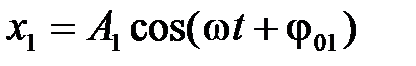 , (2.33)
, (2.33)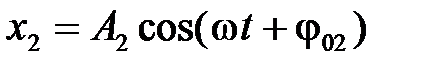 . (2.34)
. (2.34)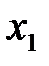 и
и 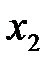 и будет также гармоническим колебанием той же циклической частоты
и будет также гармоническим колебанием той же циклической частоты 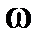 [3]
[3] 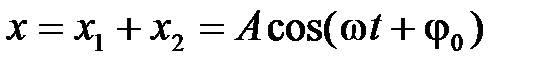 .
. 
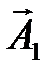 и
и 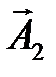 под углами j01 и j02 к оси
под углами j01 и j02 к оси 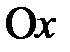 (рис. 2.9) и приведем их во вращение с угловой скоростью
(рис. 2.9) и приведем их во вращение с угловой скоростью 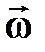 .
.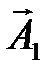 и
и 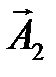 на ось
на ось 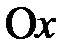 при этом совершают гармонические колебания в соответствии с уравнениями (2.33, 2.34). Результирующее колебание будет изображаться проекцией на ось
при этом совершают гармонические колебания в соответствии с уравнениями (2.33, 2.34). Результирующее колебание будет изображаться проекцией на ось 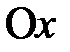 вектора
вектора 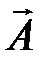 , полученного из векторов
, полученного из векторов 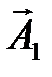 и
и 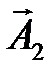 по правилу параллелограмма [3]. Из построения на рис. 2.9 и теоремы косинусов следует, что
по правилу параллелограмма [3]. Из построения на рис. 2.9 и теоремы косинусов следует, что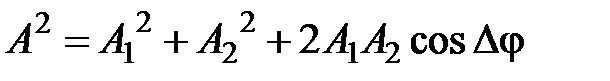 , (2.35)
, (2.35)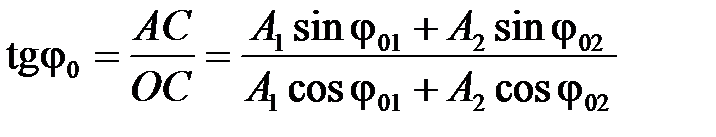 , (2.36)
, (2.36)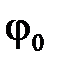 – начальная фаза результирующего колебания.
– начальная фаза результирующего колебания.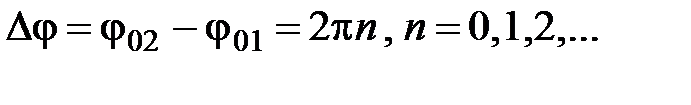
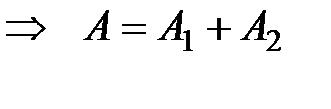 ,
,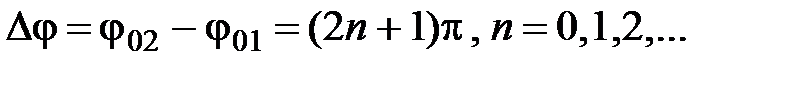
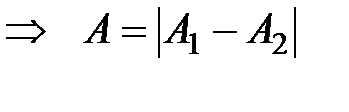 ,
,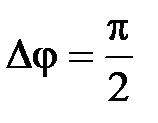
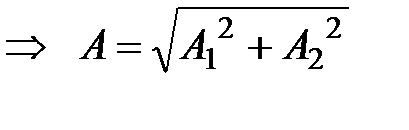 .
.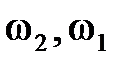 >>
>> 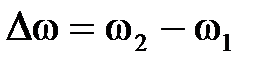 ) и равными амплитудами (для удобства расчетов):
) и равными амплитудами (для удобства расчетов):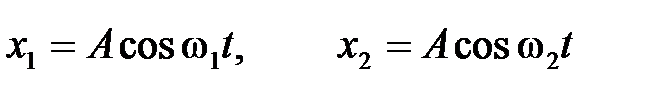 .
.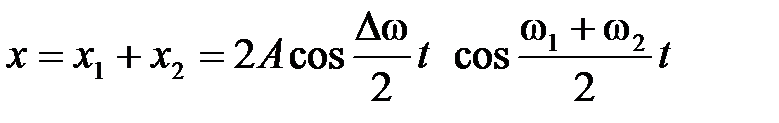 , (2.37)
, (2.37)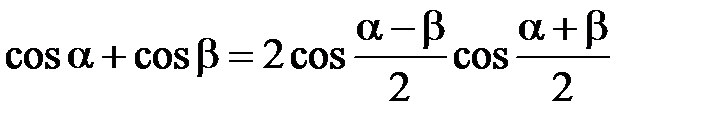 ).
).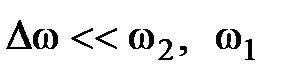 ), поэтому можно считать, что результирующее колебание
), поэтому можно считать, что результирующее колебание 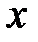 представляет собой колебание с циклической частотой
представляет собой колебание с циклической частотой 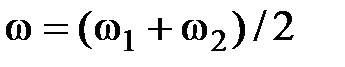 и с изменяющейся со временем амплитудой [3]
и с изменяющейся со временем амплитудой [3]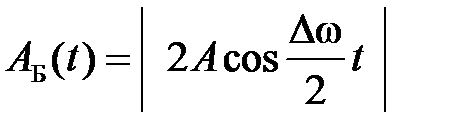 . (2.38)
. (2.38)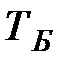 биений – понимают период изменения амплитуды результирующего колебания:
биений – понимают период изменения амплитуды результирующего колебания: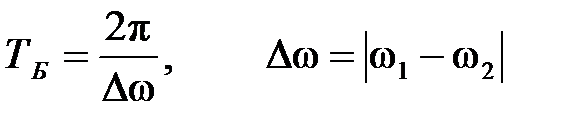 , (2.39)
, (2.39)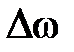 – циклическая частота биений [3].
– циклическая частота биений [3]. и смещения
и смещения  м.т. от времени t [3].
м.т. от времени t [3].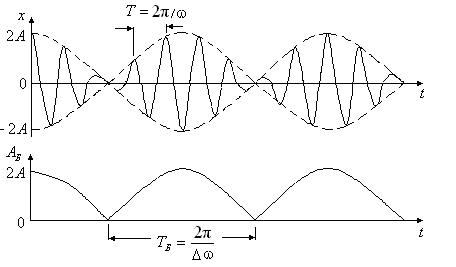
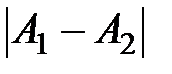 до (
до (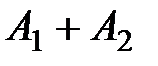 ).
).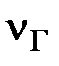 этих колебаний можно изменять) и гармонические колебания с неизвестной частотой
этих колебаний можно изменять) и гармонические колебания с неизвестной частотой 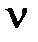 от какого-либо источника. По наблюдаемой на экране осциллографа картине биений определяют период биений
от какого-либо источника. По наблюдаемой на экране осциллографа картине биений определяют период биений 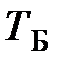 и частоту колебаний (
и частоту колебаний (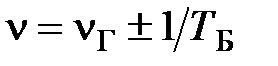 ) [3].
) [3].


