
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Микрочастица в бесконечно глубокой прямоугольной потенциальной яме
Потенциальной ямой называется область пространства, в которой потенциальная энергия частицы много меньше, чем в соседних областях. Постановка задачи. Рассмотрим одномерную задачу о движении частицы в силовом поле, в котором потенциальная энергия частицы задана следующими соотношениями [4]: Вид потенциального поля приведен на рис. 5.6, а. Видно, что частица находится в бесконечно глубокой потенциальной яме (
Рис. 5.6 Решение уравнения Шредингера. Так как микрочастица локализована в области
Решением этого уравнения является сумма двух плоских монохроматических волн де Бройля (бегущей и отраженной)
Учитывая, что волновая функция должна быть непрерывна, запишем граничные условия в этой задаче:
В формулу для волновой функции входит номер квантового состояния Используя условие нормировки, находим постоянную
Таким образом, собственные волновые функции, описывающие поведение частицы в бесконечно глубокой потенциальной яме, имеют вид Для собственных значений энергии частицы получим:
Анализ полученного решения. Из формулы (5.14) следует, что энергетический спектр частицы является дискретным (энергия частицы может принимать только определенные значения) и расходящимся, минимальное значение энергии отлично от нуля и равно Состояние частицы при квантовом числе Для сравнения: в классической механике энергетический спектр частицы является непрерывным (энергия может принимать абсолютно любые значения), минимальное значение энергии равно нулю.
Как видно, выводы классической и квантовой механики при малых значениях квантового числа Обсудим теперь вероятность обнаружения микрочастицы внутри потенциальной ямы. В классической механике частица движется равномерно по траектории от одной стенки до другой, и поэтому классическая плотность вероятности обнаружения частицы будет одинаковой во всех точках потенциальной ямы, так как частица одинаковое время находится вблизи любой точки [4]. Запишем формулу для квантовой плотности вероятности обнаружения микрочастицы внутри потенциальной ямы Из формулы (5.16) следует, что квантовая плотность вероятности обнаружения микрочастицы внутри потенциальной ямы зависит от координаты x и от номера квантового состояния n. Так, например, для квантового состояния с Вероятность обнаружения частицы в квантовом состоянии Итак, движение частицы внутри потенциальной ямы при небольших значениях
Причем для больших n происходит относительное сближение энергетических уровней, энергетический спектр становится квазинепрерывным Большое число максимумов и минимумов на графике зависимости плотности вероятности от координаты Cсоответствие выводов квантовой и классической теории при больших значениях квантовых чисел, является частным случаем принципа соответствия, согласно которому: при больших значениях квантовых чисел выводы квантовой механики должны соответствовать выводам классической механики [4]. Туннельный эффект Потенциальным барьером называется область пространства, в которой потенциальная энергия частицы больше, чем в соседних областях. Постановка задачи. Рассмотрим одномерную задачу о движении частиц с энергией W вдоль оси Согласно законам классической механики все частицы, для которых W < Решение уравнения Шредингера. В квантовой механике чтобы описать движение микрочастиц, при их встрече с потенциальным барьером, необходимо решить уравнение Шредингера в трех областях (см. рис. 5.7, а). Запишем уравнение Шредингера для каждой из областей и сразу приведем их решения. Область 1:
Область 2:
Область 3:
Из решения уравнения Шредингера для второй области видно, что
Рис. 5.7 Полученные в ходе решения уравнения Шредингера для трех областей волновые функции, необходимо «сшить» на границе этих областей, т. е. наложить на волновые функции стандартные условия. На рис. 5.7, б приведен график зависимости квадрата модуля волновой функции от координаты Анализ полученного решения. При встрече микрочастиц с потенциальным барьером возникает туннельный эффект – явление проникновения частиц сквозь высокий (W < U 0) потенциальный барьер. Коэффициент прозрачности D потенциального барьера – величина, определяющая вероятность проникновения частиц сквозь потенциальный барьер и равная отношению интенсивности волны, прошедшей потенциальный барьер, к интенсивности волны, падающей на барьер. Это отношение интенсивностей волн можно найти с учетом условий сшивания, накладываемых на волновую функцию на границах потенциального барьера (см. рис. 5.7) [4]
Как следует из формулы (5.19), коэффициент прозрачности прямоугольного потенциального барьера зависит от массы частицы ( В случае потенциального барьера Туннельный эффект объясняет многие наблюдаемые на опыте явления, такие например, как Вопросы и задания для самоконтроля к лекции 15 1. Запишите стационарное уравнение Шредингера и поясните все входящие в него величины. 2. Сформулируйте определение потенциальной ямы. Каким энергетическим спектром обладает микрочастица, находящая внутри бесконечно глубокой потенциальной ямы?
4. Сформулируйте определение потенциального барьера. В чем состоит туннельный эффект? 5. К потенциальному барьеру высотой U 0 > W и шириной d приближаются различные частицы с энергией одинаковой W: электрон, атом гелия, и молекула водорода. Для какой частицы коэффициент прозрачности барьера будет наименьшим? Основы физики атомного ядра Лекция 16 Основные понятия и законы, которые должны быть освоены в ходе лекции: ядерные силы и их свойства, дефект масс, энергия связи, удельная энергия связи; a-, b- и g-распады; основной закон радиоактивного распада, период и постоянная распада, среднее время жизни и активность радиоактивного ядра,; ядерные реакции и их энергия.
|
|||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.86.134 (0.016 с.) |
 (5.12)
(5.12) ), за пределы которой она выйти не может.
), за пределы которой она выйти не может.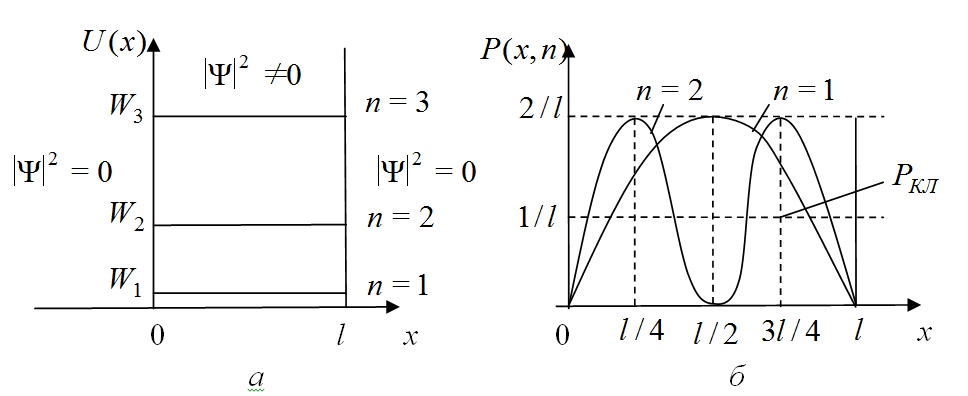
 , то уравнение Шредингера необходимо решать именно для этой области. Запишем уравнение Шредингера, учитывая, что в области ямы
, то уравнение Шредингера необходимо решать именно для этой области. Запишем уравнение Шредингера, учитывая, что в области ямы 
 .
.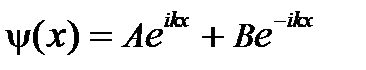 .
.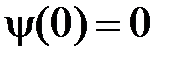 ,
,  . Подставляя данные граничные условия в волновую функцию, получим ее явный вид:
. Подставляя данные граничные условия в волновую функцию, получим ее явный вид: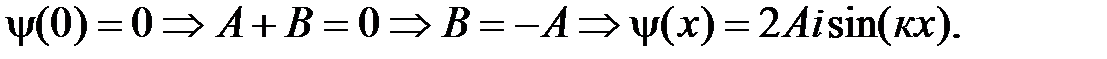

 , причем значение
, причем значение  исключается, так как
исключается, так как 
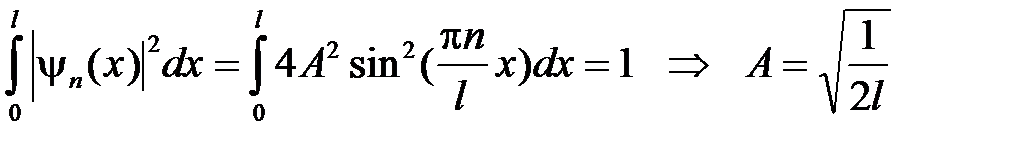 .
. (5.13)
(5.13)
 ,
,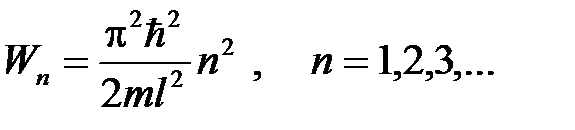 (5.14)
(5.14) (рис. 5.6, а)
(рис. 5.6, а) ,
, 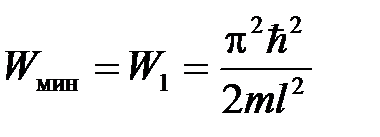 . (5.15)
. (5.15) = 1, называется основным состоянием частицы, а все остальные ее состояния называются возбужденными.
= 1, называется основным состоянием частицы, а все остальные ее состояния называются возбужденными. находятся в несоответствии между собой [4].
находятся в несоответствии между собой [4]. . (5.16)
. (5.16) плотность вероятности
плотность вероятности 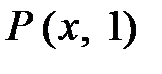 на краях потенциальной ямы равна нулю, а в ее середине будет максимальной. Число максимумов на зависимости
на краях потенциальной ямы равна нулю, а в ее середине будет максимальной. Число максимумов на зависимости 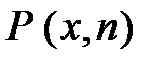 будет равно номеру квантового состояния
будет равно номеру квантового состояния  , а вся площадь под каждым графиком плотности вероятности равна единице (рис. 5.6, б), так как физический смысл площади под всем графиком – вероятность обнаружения частицы внутри ямы.
, а вся площадь под каждым графиком плотности вероятности равна единице (рис. 5.6, б), так как физический смысл площади под всем графиком – вероятность обнаружения частицы внутри ямы. равна площади под графиком соответствующей плотности вероятности
равна площади под графиком соответствующей плотности вероятности  и ограниченной по оси абсцисс значениями l 1 и l 2, а также может быть вычислена по формуле
и ограниченной по оси абсцисс значениями l 1 и l 2, а также может быть вычислена по формуле (5.17)
(5.17) необходимо описывать в рамках квантовой механики. Однако, при больших значениях квантового числа n возможно применение классической механики при описании движения микрочастицы. Это связано с тем, что при увеличении n возрастает модуль волнового вектора
необходимо описывать в рамках квантовой механики. Однако, при больших значениях квантового числа n возможно применение классической механики при описании движения микрочастицы. Это связано с тем, что при увеличении n возрастает модуль волнового вектора  (
(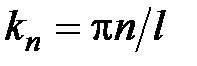 ), следовательно, уменьшается длина волны де Бройля (
), следовательно, уменьшается длина волны де Бройля (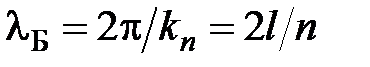 ), соответствующая движению частицы, и при некотором значении n будет выполняться условие применимости классической механики для описания движения микрочастицы:
), соответствующая движению частицы, и при некотором значении n будет выполняться условие применимости классической механики для описания движения микрочастицы:  <<
<<  [4].
[4].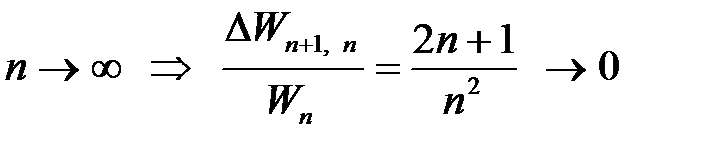 ,
,  (5.18)
(5.18)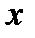 (при большом n) приводит к тому, что усредненное значение <
(при большом n) приводит к тому, что усредненное значение < 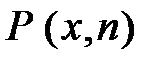 > квантовой плотности вероятности будет совпадать с классическим значением плотности вероятности.
> квантовой плотности вероятности будет совпадать с классическим значением плотности вероятности. . Частицы из области 1 налетают на прямоугольный потенциальный барьер (область 2) высотой
. Частицы из области 1 налетают на прямоугольный потенциальный барьер (область 2) высотой 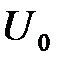 , причем W <
, причем W <  (см. рис. 5.7, а). Что же происходит с частицами при их встрече с потенциальным барьером?
(см. рис. 5.7, а). Что же происходит с частицами при их встрече с потенциальным барьером?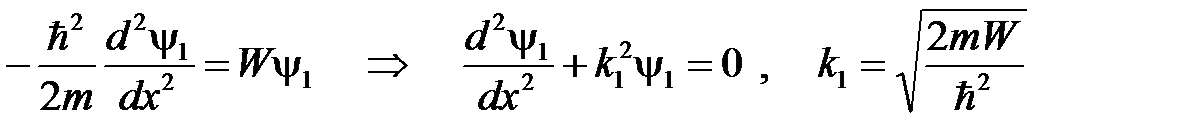 ,
,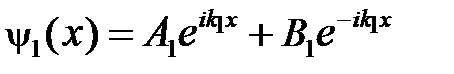 .
. ,
, .
. ,
,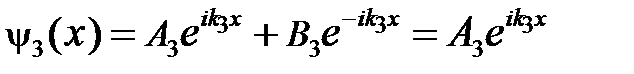 ,
,  .
. не носит волнового характера, т. е. ее нельзя представить в виде гармонической функции синуса (косинуса). Это означает, что частица не может находиться в этой области сколь угодно долго, по истечении определенного промежутка времени она должна покинуть эту область пространства [4]. В третьей области пространства отражения нет, поэтому отраженной волны в области не будет.
не носит волнового характера, т. е. ее нельзя представить в виде гармонической функции синуса (косинуса). Это означает, что частица не может находиться в этой области сколь угодно долго, по истечении определенного промежутка времени она должна покинуть эту область пространства [4]. В третьей области пространства отражения нет, поэтому отраженной волны в области не будет.
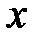 с учетом стандартных условий (условий сшивания), накладываемых на волновые функции на границах потенциального барьера. Из рис. 5.7, б видно, что вероятность обнаружения микрочастицы внутри потенциального барьера (вторая область) уменьшается с ростом координаты
с учетом стандартных условий (условий сшивания), накладываемых на волновые функции на границах потенциального барьера. Из рис. 5.7, б видно, что вероятность обнаружения микрочастицы внутри потенциального барьера (вторая область) уменьшается с ростом координаты  и что вероятность найти микрочастицу в области 3 (область за барьером) будет отлична от нуля [4].
и что вероятность найти микрочастицу в области 3 (область за барьером) будет отлична от нуля [4]. . (5.19)
. (5.19)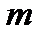 ), ширины барьера (
), ширины барьера (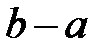 ) и соотношения между высотой потенциального барьера и полной энергией налетающей на него частицы (
) и соотношения между высотой потенциального барьера и полной энергией налетающей на него частицы (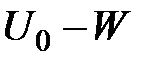 ).
). произвольной формы (рис. 5.7, в), коэффициент прозрачности барьера определяется по формуле:
произвольной формы (рис. 5.7, в), коэффициент прозрачности барьера определяется по формуле: . (5.20)
. (5.20)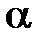 -распад ядер, холодную эмиссию электронов из металла.
-распад ядер, холодную эмиссию электронов из металла.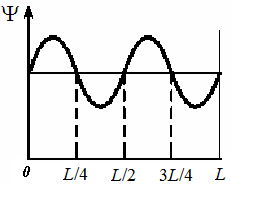 3. Протон находится в потенциальной яме с бесконечно высокими стенками. Волновая функция, описывающая его состояние имеет вид указанный на рисунке. Чему равна вероятность обнаружить протон на участке
3. Протон находится в потенциальной яме с бесконечно высокими стенками. Волновая функция, описывающая его состояние имеет вид указанный на рисунке. Чему равна вероятность обнаружить протон на участке  ?
?


