
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Московский авиационный институтСодержание книги
Поиск на нашем сайте
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ) МАИ ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА. ХИМИЧЕСКАЯ КИНЕТИКА. ФИЗИКО-ХИМИЧЕСКИЕ МЕТОДЫ АНАЛИЗА Учебное пособие к лабораторному практикуму по химии Под ред. канд. хим. наук Н.С. Будановой и А.А. Фармаковской Утверждено На заседании редсовета Октября 2007 г. М О С К В А Издательство МАИ−ПРИНТ 2009 ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА. ХИМИЧЕСКАЯ КИНЕТИКА. ФИЗИКО-ХИМИЧЕСКИЕ МЕТОДЫ АНАЛИЗА: Учебное пособие к лаб. практикуму по химии Под ред. Н.С. Будановой и А.А. Фармаковской.
− М.: Изд−во МАИ−ПРИНТ, 2009. − 95 с. ил.
Авторы: Н. С. Буданова, В. Н. Гразлов, С. И Селиванова, М. А Семенова, В. А Новожилов, А. А. Фармаковская, Н. П. Жарова, Г. Н. Устюжанинова.
Пособие содержит теоретические введения и описания лабораторных работ по двум основным разделам курса химии: «Химическая термодинамика» и «Химическая кинетика», а также по некоторым часто использующимся в аналитической практике физико-химическим методам анализа. В разделе «Растворы» рассмотрены вопросы, равновесия в растворах неэлектролитов и электролитов, буферные растворы, коллоидные растворы, адсорбционное равновесие, ионообменная хроматография. Раздел «Электрохимия» посвящен вопросам, связанным с теорией гальванических элементов, электролиза, коррозии, а также практическому применению электрохимических методов анализа. Пособие предназначено для студентов I курса всех технических факультетов МАИ дневной и вечерней форм обучения.
Рецензенты:
кафедра физики и физической химии Военно-инженерной академии им. Н.Е. Жуковского (зав. кафедрой профессор В. В. Чернышев); доктор химич. наук, профессор Н. Н. Желиговская (МГУ). РАЗДЕЛ I. ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
Химическая термодинамика изучает переходы энергии из одной формы в другую при химических реакциях и устанавливает направления и пределы их самопроизвольного протекания при заданных условиях. Объектом изучения в термодинамике является система. Под системой понимают вещество или группу взаимодействующих веществ, физически или мысленно обособленных от окружающей среды. К изолированным относятся те системы, которые не обмениваются массой и энергией с внешней средой. Если через границу, отделяющую систему от внешней среды, может осуществляться обмен веществом между системой и внешней средой, система называется открытой; если обмен веществом невозможен – система закрытая. Системы бывают гомогенными (однофазными), обладающими одинаковыми физическими и химическими свойствами в любой части объема, и гетерогенными, характеризующимися наличием поверхностей раздела, отделяющих части системы (фазы), различные по свойствам. Состояние системы описывается термодинамическими параметрами – температурой, давлением, объемом, концентрацией. Изменение термодинамических параметров состояния системы приводит к возникновению термодинамического процесса. Термодинамические функции, значения которых зависят от состояния системы, называются функциями состояния, и их изменения в каком-нибудь процессе зависят только от начального и конечного состояния системы и не зависят от пути перехода системы из одного состояния в другое. К важнейшим функциям состояния, характеризующим химические системы, относятся внутренняя энергия U, энтальпия H, энтропия S и энергия Гиббса G (изобарно-изотермический потенциал).
Первый закон термодинамики
Первый закон термодинамики может быть сформулирован следующим образом: «Каждая система обладает некоторым запасом внутренней энергии U, мерой изменений которой при обратимых процессах служит теплота q, поглощаемая системой, и работа А, совершаемая системой».
∆U = Q-A. (1.1) Механическая работа, совершаемая системой против внешнего давления, равна произведению этого давления на изменение объема: A = p∙∆V. Если объем в процессе перехода системы из состояния 1 в состояние 2 не меняется (V = const – изохорный процесс), то система не совершает работы, а изменение внутренней энергии равно тепловой энергии, выделяемой или поглощаемой системой:
∆U = Qv. (1.2)
Для изобарного процесса (р = const) изменение внутренней энергии при переходе системы из состояния 1 в состояние 2
∆U= Qр- p∙∆V,
откуда
Qр =∆U+p∆V.
Если р = const, то Qр = ∆(U+p∙V), где H = U+p∙V энтальпия, являющаяся функцией состояния, тогда
QP = ∆H (1. 3)
и тепловой эффект изобарного процесса определяется изменением энтальпии системы. Физический смысл энтальпии состоит в том, что она характеризует тепловой эффект реакций, протекающих в изобарных условиях. Из уравнений (1.2) и (1.3) можно записать
QP - Qv = ∆U+p∙∆V-∆U = p∙∆V. (1.4)
Из уравнения Менделеева−Клайперона p∙∆V = ∆n∙R∙T, откуда
QP - Qv = ∆n∙R∙T, (1.5) где ∆n − изменение числа молей в процессе реакции. Тепловые эффекты реакций Qv и QP измеряются экспериментально или вычисляются. Увеличение ∆U и ∆Н соответствует эндотермическому процессу (тепло поглощается), а их уменьшение − экзотермическому процессу (тепло выделяется). Второй закон термодинамики Второй закон термодинамики позволяет определить возможность протекания и направление процесса в изолированных системах при данных условиях. Для изолированных систем критерием, который характеризует возможность, направление и предел самопроизвольного протекания термодинамических процессов, служит особая функция состояния – энтропия S. Энтропия является мерой вероятности состояния системы. Она возрастает при переходе вещества из более упорядоченного состояния в менее упорядоченное, например при переходе вещества из кристаллического состояния в жидкое и из жидкого в газообразное, при растворении кристаллов, при расширении газов. Все процессы, в результате которых упорядоченность системы возрастает, сопровождаются уменьшением энтропии. Согласно второму закону термодинамики в изолированных системах могут совершаться только такие процессы, при которых энтропия системы возрастает, и подобный самопроизвольный процесс может идти только до такого состояния, при котором энтропия обладает максимальным значением (для данных условий). Изменение энтропии при обратимом превращении и постоянной температуре может быть выражено уравнением Обратимым превращением является бесконечно медленный переход системы из одного равновесного состояния в другое через непрерывный ряд равновесных состояний. При обратимом протекании процесса система все время находится в состоянии термодинамического равновесия, когда значения ее параметров в каждый момент одинаковы в любой точке и не меняются во времени. Для необратимых процессов
Самопроизвольно протекающие процессы необратимы, т.е. систему нельзя вернуть в исходное состояние, не производя каких-либо изменений в ней самой или в окружающей среде. Поскольку энтропия – функция состояния, ее изменение не зависит от того, как протекает процесс: обратимо или необратимо. Из (1.11) и (1.12) следует, что В изолированной системе Изменение энтропии в химических процессах вычисляется так же, как и изменение любой функции состояния:
В отличие от энтальпии образования энтропия простого вещества не равна нулю. На практике чаще всего имеют дело с закрытыми системами, которые обмениваются с внешней средой энергией, но не обмениваются веществом. Для такой реальной системы, находящейся при постоянной температуре и давлении, критерием направленности процесса является функция состояния, называемая изобарно-изотермическим потенциалом, или энергией Гиббса, и определяемая по уравнению ∆G = ∆H - T∆S. (1.14) Для изобарно-изотермических процессов условием равновесия будет ∆G = 0. Условием самопроизвольного протекания процесса − ∆G < 0. При ∆G > 0 реагенты не могут превращаться в продукты, а принципиально возможна обратная реакция – превращение продуктов в реагенты. Стандартный изобарно-изотермический потенциал образования соединения
Вопросы и задачи к главе 1 1. Что такое термодинамическая система? Какие вы знаете типы систем? 2. В чем сущность первого закона термодинамики? 3. Чему равен тепловой эффект изобарного и изохорного процессов? 4. Как формулируется закон Гесса и какие следствия из него вытекают? 5. Что такое функции состояния? 6. Что называется стандартной теплотой образования и сгорания? 7. В чем сущность второго закона термодинамики? 8. Что такое термодинамически обратимые и необратимые процессы? 9. Каков физический смысл энтропии? 10. Что такое изобарно-изотермический потенциал и как его можно вычислить? 11. Пользуясь теплотами образования, рассчитайте тепловой эффект следующих реакций в стандартных условиях: CO(r) + H2O(r) = CO2(r) + H2(r); Fl2O3(k) + 2Al(k) = Al2O3(k) + 2Fl(k). CO(r) - 110,6 H2O(r) - 241,98 CO2(r) - 393,8 Fl2O3(k) - 822,7 Al2O3(k) - 1676,8 Ответ: - 41,2 кДж, - 854,1 кДж. Рассчитайте 3H2(r) + N2(r) = 2NH3(r)
Ответ: - 206,8 кДж/моль град Рассчитайте изменение энтальпии, энтропии и энергии Гиббса для реакции окисления NO в NO2 в стандартных условиях; 2NO + О2 = 2NO2 NO 90,31 NO 210,7 NO2 33,00 NO2 240,2 O2 0 O2 205,0 Ответ:
Порядок выполнения работы Оборудование 1. Калориметр (рис. 1.1). 2. Бюретка. Порядок выполнения работы 1. Налить во внутренний стакан калориметра 40 мл титруемого раствора щелочи. 2. Опустить в раствор стеклянную мешалку и термометр Бекмана. 3. В течение 2-3 минут наблюдать за температурой, которая практически не должна измениться. 4. Опустить в калориметр кончик бюретки с титрующим раствором кислоты так, чтобы раствор из нее не попадал на термометр. 5. Приливать титрующий раствор к титруемому непрерывно и с постоянной скоростью, все время размешивая мешалкой. Записывать показания термометра Бекмана после каждого прилитого миллилитра. 6. На основании полученных данных построить график в координатах «температура − объем титрующего раствора в миллилитрах». 7. По перегибу кривой приближенно определить точку эквивалентности (обычно она лежит в интервале объемов 3-8 мл). 8. Провести по вышеописанной методике точный опыт, при котором записывать температуру через каждые 0,5 мл прилитого раствора кислоты. 9. Результаты нанести на график и уже точно определить точку эквивалентности. 10. Рассчитать концентрацию раствора щелочи.
ГЛАВА 2. ХИМИЧЕСКОЕ РАВНОВЕСИЕ Состояние химического равновесия определяется двумя признаками: ● если система находится в состоянии равновесия, то состав ее с течением времени при постоянных внешних условиях не изменяется; ● если система, находящаяся в равновесии, будет выведена из этого состояния вследствие внешних воздействий, то с прекращением их действий она возвратится в прежнее состояние. Химическое равновесие наступает в том случае, когда энтропия достигает максимума (для изолированных систем) или изобарно-изотермический потенциал – минимума (для открытых систем).
Адсорбционное равновесие
Процесс поглощения одного вещества поверхностью или объемом другого называется сорбцией. Сорбция, происходящая только на поверхности тела, называется адсорбцией. Величина адсорбции зависит от природы поглотителя (адсорбента) и поглощаемого вещества (адсорбата), от температуры и давления газа или концентрации растворов. В качестве адсорбентов применяют вещества, обладающие большой удельной площадью поверхности. Высокодисперсными адсорбентами являются активированный уголь, силикагель, глина, целлюлоза и другие материалы. Процесс отрыва частиц адсорбата от поверхности адсорбента, т.е. явление, обратное адсорбции, называют десорбцией. Если в системе «адсорбат – адсорбент» при заданных условиях скорость адсорбции равна скорости десорбции, состояние системы называют адсорбционным равновесием. Количественно адсорбцию выражают в молях адсорбата на единицу площади поверхности адсорбента, моль/м2. Поверхность адсорбента, на которой могут размещаться молекулы адсорбата, ограничена. Поэтому величина адсорбции не может превышать предельного значения Г = Г∞ . Соотношение Г / Г∞ называют степенью заполнения поверхности адсорбента данным адсорбатом Соответственно (Ө = 1) будет означать полное заполнение площади поверхности адсорбента адсорбатом. Равновесие между веществом, находящимся в адсорбированном состоянии на поверхности, и этим же веществом в растворе, характеризуется константой адсорбционного равновесия
где Ө − степень заполнения поверхности адсорбированным веществом; с – равновесная концентрация. С учетом соотношения (2.8) уравнение (2.9) может быть представлено в виде уравнения изотермы адсорбции Лэнгмюра Графически изотерма адсорбции Лэнгмюра, построенная в координатах Г = f(С), представляет собой гиперболу (рис. 2.1).
В области малых концентраций происходит линейное увеличение адсорбции с увеличением концентрации; в области больших концентраций адсорбция достигает предельного значения, равного адсорбции при полном заполнении поверхности мономолекулярным слоем Г∞. Значения Г∞ и Кадс можно определить графически по уравнению Лэнгмюра (2.10), преобразовав его в уравнение прямой линии Полученную численную зависимость представляют в виде графика в координатах Экспериментальные точки должны укладываться на прямую с наклоном а = tgφ = b = Г∞ =
Вопросы и задачи к главе 2
1. Каковы условия термодинамического равновесия? 2. Что такое константа равновесия и от чего она зависит? 3. Как выражается зависимость константы равновесия от температуры? 4. Какие факторы влияют на смещение химического равновесия? 5. Что называется адсорбцией? 6. Что такое адсорбционное равновесие? 7. Как зависит адсорбция от концентрации при постоянной температуре? 8. Какую зависимость выражает уравнение Лэнгмюра? Порядок выполнения работы
1. Взвесить сосуд (9) с исследуемым веществом (этиловый спирт, серный эфир) на аналитических весах (тубусы 5 и 7 должны быть закрыты пробками). 2. Собрать установку по приведенной схеме и погрузить сосуд в термостат. 3. Измерить температуру в термостате и атмосферное давление р. 4. При закрытом кране (2) влить в воронку 3,5 л воды (объем определить мерным цилиндром). 5. Открыть кран (2) и, отрегулировав скорость тока воздуха краном (4), следить за вытеканием воды из воронки (3). 6. Измерить избыточное давление 7. Когда вода из воронки (3) вытечет, закрыть кран (2), подождать, пока не окончится прохождение пузырьков воздуха через сосуд (9), извлечь его, закрыть тубусы пробками, вытереть фильтровальной бумагой и взвесить на аналитических весах. Проверить температуру и атмосферное давление. В случае изменения показаний, установленных в начале эксперимента, взять для расчетов средние значения.
Расчетная часть
Давление насыщенного пара вещества вычисляется по уравнению состояния идеального газа, причем предполагается, что смесь пара вещества с воздухом подчиняется закону Дальтона. Число молей сухого воздуха, прошедшего через сосуд вычисляется по формуле
где V − объем вытесненного из газометра воздуха; р − атмосферное давление (показание барометра); Это количество воздуха увлекает за собой По закону Дальтона парциальное давление газа (пара) равно его мольной доле, умноженной на общее давление. Смесь пара с воздухом покидает сосуд (9) при общем давлении
Давление пара необходимо определить при двух температурах и по уравнению (2.13) рассчитать теплоту испарения.
Таблица
Оборудование и реактивы 1. Термостат. 2. 4 конические колбы для титрования емкостью 100 мл. 3. 2 колбы с притертыми пробками емкостью 100 мл. 4. Пипетка на 15 мл. 5. 0,0128 М раствор сульфата железа (III) Fe2(SO4)2 . 6. 0,025 М раствор иодида калияKI. 7. Бюретка с 0,015 М раствором тиосульфата натрия Na2S2O3. 8. Раствор крахмала. 9. Баня со льдом. Порядок выполнения работы Для проведения реакции необходимо задаться определенным исходным составом реагирующей смеси (вариант I или вариант II):
1. Налить в две сухие колбы с притертыми пробками емкостью100 мл выбранные количества растворов исходных веществ. 2. Поместить колбы на 30 мин в водяной термостат при температуре 25оС. 3. За это время приготовить для титрования 4 конические колбы емкостью 100 мл, в каждую из которых налить по 30 мл дистиллированной воды и поставить их на лед. 4. По истечении 30 мин слить вместе содержимое колб 1 и 2 (момент слива отметить по часам), закрыть реакционную колбу пробкой и установить в термостат. 5. Определить момент наступления равновесия в реакционной смеси, для чего: 5.1. Через определенные промежутки времени от начала реакции (15, 30, 45 мин), не вынимая колбу из термостата, отобрать пипеткой пробу (15 мл) и перенести ее в охлажденную коническую колбу для титрования. Временем отбора пробы считать момент слива раствора из пипетки в колбу для титрования. 5.2. Сразу же после сливания пробы оттитровать выделившийся иод 0,015 М раствором тиосульфата натрия Na2S2O3 до бледно-желтой окраски раствора. 5.3. Добавить в раствор несколько капель раствора крахмала и продолжать титровать раствором тиосульфата до исчезновения синей окраски (светло-синяя окраска раствора, появляющаяся через некоторое время после титрования, не учитывается). 5.4. Перед отбором следующей пробы сполоснуть пипетку дистиллированной водой. 6. Построить график зависимости объема раствора тиосульфата, пошедшего на титрование проб от времени τ. Моменту наступления равновесия будет отвечать точка перегиба на кривой. 7. Рассчитать равновесную концентрацию иода по формуле, вытекающей из закона эквивалентов где
8. Рассчитать равновесный состав смеси, построив следующую таблицу:
9. Рассчитать константу равновесия К при температуре опыта Т1, используя найденные значения равновесных концентраций участников реакции по формуле закона действия масс:
10. В такой же последовательности (пункты 1.9) провести опыт при температуре Т2 и рассчитать константу равновесия при этой температуре 11. Рассчитать стандартные термодинамические параметры реакции: ● тепловой эффект ΔН0 по формуле ● изобарно-изотермический потенциал реакции (изменение свободной энергии Гиббса)
● изменение энтропии реакции: Оборудование 1. Коническая колба для растворения соли. 2. Воронка, бумажные фильтры. 3. Сосуд для измерения электропроводности. 4. Реохордный мост или кондуктометр. 5. Термостат. Порядок выполнения работы
1. Небольшое количество труднорастворимой соли тщательно растереть в ступке и перенести в коническую колбу с притертой пробкой, промыть соль два-три раза дистиллированной водой для удаления легкорастворимых примесей. 2. Отмытую соль залить 100 мл дистиллированной воды и, плотно закрыв пробкой, непрерывно перемешивать в течение 20 мин. Полученной суспензии дать отстояться. 3. После отстаивания осадка часть раствора слить в сосуд для измерения электропроводности и измерить сопротивление раствора 4. Оставшийся раствор с осадком поместить в термостат и выдержать в нем не менее 20 мин, при температуре Т2 = 40°С. 5. Часть горячего раствора слить в сосуд для измерения электропроводности и измерить сопротивление раствора 6. Рассчитать растворимость соли Sпри температурах Т1и Т2, полагая, что æ р-ра = 7. Определить величины произведения растворимости 8. Рассчитать
Оборудование 1. Термостат. 2. Четыре колбы на 250 мл каждая. 3. Четыре конические колбы для титрования. 4. Воронки, фильтровальная бумага. 5. Бюретка.
Порядок выполнения работы
Работу выполняют две пары студентов. Измерения проводят при комнатной температуре и при 40°С. Полученные каждой парой студентов результаты используются для расчетов теплоты адсорбции Hадс.
1. В четыре колбы налить по 25 мл растворов уксусной кислоты различных концентраций и внести в них по 0,5 г активированного угля, предварительно измельченного в ступке. Интенсивно взболтать содержимое колб и выдержать для достижения равновесия в течение 30 мин., постоянно помешивая растворы (для опыта при повышенной температуре использовать термостат). 2. Растворы с углем отфильтровать. 3. От каждого фильтрата отобрать пипеткой по 10 мл раствора в колбы для титрования. 4. Пробы титровать раствором NaOHизвестной концентрацией Nщс индикатором фенолфталеин, предварительно внеся его по три капли на каждую пробу. Титрующий раствор прибавлять по каплям до появления устойчивой светло-розовой окраски. 5. По результатам титрования рассчитать равновесную концентрацию уксусной кислоты, установившуюся после адсорбции:
6. Занести рассчитанные величины в таблицу. 7. По разности исходной и равновесной концентраций рассчитать величину адсорбции как число грамм-эквивалентов кислоты, поглощенной 1г угля:
где Сисх − исходная концентрация кислоты, г-экв/л; Сравн −равновесная концентрация кислоты, г-экв/л; Vр-ра −объем раствора кислоты, взятой для адсорбции, л; m− масса активированного угля, г. 8. По полученным данным построить изотерму адсорбции Г = f(Сравн)и линеаризованную изотерму 9. Рассчитать графически Г∞ и Кадс . 10. По величинам констант адсорбции при двух температурах рассчитать теплоту адсорбцииΔHадс по уравнению Вант-Гоффа:
где R = 8,314 Дж/моль∙К. Таблица
Влияние катализаторов Для многих реакций можно подобрать такое вещество, которое, присутствуя даже в небольшом количестве в смеси веществ, способствует химической реакции. Такие вещества, которые обязательно участвуют в процессе, но в конце реакции регенерируются и остаются химически неизменными, называются катализаторами. Поскольку принципиальная осуществимость и пределы протекания реакции определяются величиной и знаком изобарно-изотермического потенциала (∆G < 0), катализатор лишь ускоряет время достижения равновесного состояния, но не изменяет его. Действие катализаторов объясняется главным образом тем, что они уменьшают энергию активации реакции. В зависимости от того, находится ли катализатор в той же фазе, что и реагирующее вещество, или образует самостоятельную фазу, говорят о гомогенном или гетерогенном катализе. Механизм каталитического действия для них неодинаков, однако и в том и в другом случае происходит ускорение реакции за счет снижения Еакт. Для гомогенных реакций считают, что катализатор образует в той же фазе промежуточные реакционно-способные продукты. Медленно протекающий процесс, например реакция А + В = АВ в присутствии катализатора происходит в две стадии: А + К = АКи АК + В = АВ + К, т.е. сначала образуются частицы промежуточного соединения АК, которое, реагируя с веществом В, дает в итоге конечный продукт АВ с регенерацией катализатора К. При гетерогенном катализе ускорение процесса обычно связано с каталитическим действием поверхности твердого катализатора. Порядок величины ускоряющего действия катализатора может быть оценен по уравнени
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.235 (0.012 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

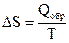 . (1.11)
. (1.11)
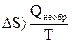 . (1.12)
. (1.12) 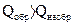 .
.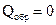 и
и 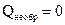 . Из этого следует, что в изолированной системе при обратимом протекании процесса
. Из этого следует, что в изолированной системе при обратимом протекании процесса 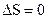 , а при необратимом
, а при необратимом 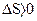 . Процессы с уменьшением энтропии, когда
. Процессы с уменьшением энтропии, когда 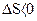 , в такой системе невозможны. Таким образом, энтропия является критерием направленности протекания процессов для изолированной системы. Процесс протекает самопроизвольно, если
, в такой системе невозможны. Таким образом, энтропия является критерием направленности протекания процессов для изолированной системы. Процесс протекает самопроизвольно, если 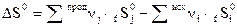 (1.13)
(1.13)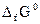 равен изменению изобарного потенциала при реакциях образования этого соединения из простых веществ в стандартных условиях (р = 1013 ГПа, Т = 298 К). Величину
равен изменению изобарного потенциала при реакциях образования этого соединения из простых веществ в стандартных условиях (р = 1013 ГПа, Т = 298 К). Величину  можно вычислить из табличных значений
можно вычислить из табличных значений 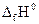 и
и 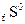 участников реакции. Свободную энергию Гиббса химической реакции, которая определяет возможность протекания любого химического превращения в стандартных условиях, можно рассчитать по уравнению
участников реакции. Свободную энергию Гиббса химической реакции, которая определяет возможность протекания любого химического превращения в стандартных условиях, можно рассчитать по уравнению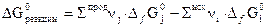 . (1.15)
. (1.15)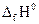 (кДж/моль);
(кДж/моль);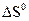 следующей реакции:
следующей реакции: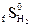 = 130,7 Дж/моль град
= 130,7 Дж/моль град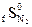 = 199,9 Дж/моль град
= 199,9 Дж/моль град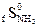 = 238,36 Дж/моль град
= 238,36 Дж/моль град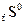 , кДж/ моль∙К
, кДж/ моль∙К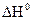 = - 56,8 кДж/ моль;
= - 56,8 кДж/ моль; 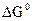 = - 29,0 кДж/ моль.
= - 29,0 кДж/ моль.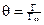 . (2.12)
. (2.12)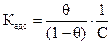 , (2.13)
, (2.13)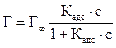 . (2.14)
. (2.14)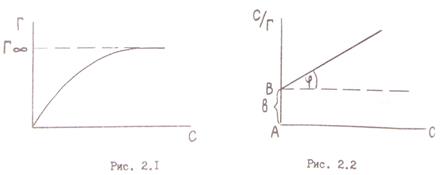
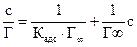 . (2.15)
. (2.15)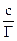 = f (с) (рис. 2.2).
= f (с) (рис. 2.2).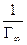 ,отсекающую на оси ординат отрезок
,отсекающую на оси ординат отрезок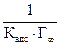 . Отсюда находят
. Отсюда находят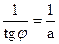 ;
; 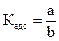 .
.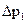 по манометру (12).
по манометру (12).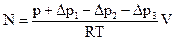 ,
,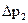 − температурная поправка;
− температурная поправка; 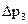 − давление насыщенных паров водыпри температуре опыта; Т − абсолютная температура в термостате; q− потеря в массе вещества (заключенного в сосуд 9 в процессе эксперимента); М– молекулярная масса вещества; р х − определяемое давление насыщенного пара.
− давление насыщенных паров водыпри температуре опыта; Т − абсолютная температура в термостате; q− потеря в массе вещества (заключенного в сосуд 9 в процессе эксперимента); М– молекулярная масса вещества; р х − определяемое давление насыщенного пара.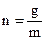 молей пара исследуемого вещества.
молей пара исследуемого вещества.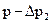 , следовательно
, следовательно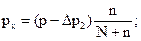
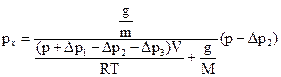 .
.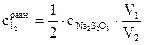 ,
,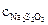 − молярная концентрация раствора тиосульфата натрия; V1 − объем раствора тиосульфата, пошедший на титрование иода в момент равновесия, мл; V2 − объем взятой пробы, мл.
− молярная концентрация раствора тиосульфата натрия; V1 − объем раствора тиосульфата, пошедший на титрование иода в момент равновесия, мл; V2 − объем взятой пробы, мл.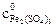
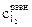
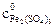
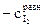
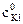
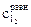
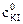
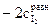
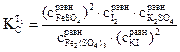 .
.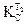 .
.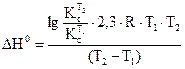 ;
;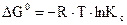 ;
;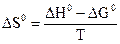 .
.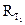 при комнатной температуре.
при комнатной температуре.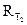 .
.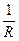 .
.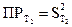 и
и 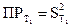 .
.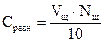 .
.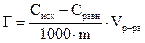 ,
,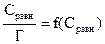 для обеих температур.
для обеих температур.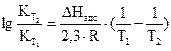 ,
,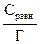 г/л
г/л



