Конические зубчатые передачи

 

Основные параметры

      

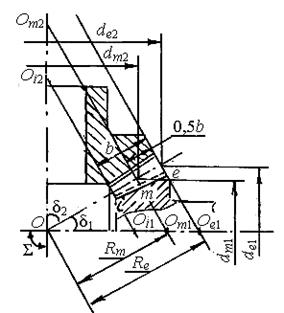
   Конические зубчатые передачи применяют для передачи энергии между пересекающимися осями валов. Наибольшее применение имеют ортогональные

передачи с межосевым углом Σ = 90° (рис. 4.10).

       Конические колеса бывают с прямыми (в открытых передачах) и круговыми (в редукторах) зубьями. Круговые зубья очерчены линиями по дугам окружности.

     Конуса с вершиной в точке О являются основными (рис.4.10). Внешние и внутренние торцы на конических зубчатых колесах формируют внешними (вершины О _е) и внутренними (вершины О _i) дополнительными конусами, образующие которых перпендикулярны образующей делительного конуса.

Расстояние между внешним (параметры обозначают с индексом е) и внутренним (параметры – с индексом i) дополнительными конусами определяет ширину b венца.      На длине 0,5 b расположен средний дополнительный конус с вершиной О m (параметры – с индексом m).      Расстояние от вершины О по образующей делительного конуса до внешнего торца е называют внешним конусным расстоянием R e, до середины ширины венца – средним конусным расстоянием R m (рис. 4.10).      Пересечения делительного конуса с дополнительными конусами определяют диаметры делительных окружностей ко-нического зубчатого колеса: d e – внеш-

-     Рис. 4.10

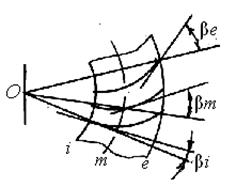
ний, d _m – средний, d _i – внутренний делительные диаметры.

     Угол наклона зубьев β определяют (рис. 4.11) углом между лучом, проведенным из вершины О, и касательной к линии зуба в рассматриваемой точке

зуба. Для прямых зубьев β = 0. У круговых зубьев угол β переменный:

    β _e > β _m > β _i. За расчетный принимают угол β _m в среднем сечении.

Рис. 4.11

Рис. 4.12         Лучше всего зарекомендовали себя передачи с круговыми зубьями с углом β m = 35°.

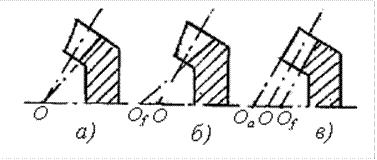
      Наличие угла наклона повышает плавность работы, контактную и изгибную прочность, уменьшает шум, но увеличивает нагрузки на опоры и валы.

     Зубья конических колес в зависимости от изменения размеров их нормальных сечений по длине выполняют в виде трех осевых форм (рис. 4.12).

      Осевая форма I - пропорционально понижающиеся зубья (рис. 4.12, а). Вершины конусов делительного и впадин совпадают, высота ножки зуба пропорциональна конусному расстоянию. Применяют для прямых зубьев.

      Осевая форма II  – нормальносужающиеся зубья (рис. 4.12, б). Вершина конуса впадин О _f расположена так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу пропорциональна конусному расстоянию. Эта форма позволяет одним инструментом обрабатывать сразу обе грани зубьев, повышая производительность. Является основной для колес с круговыми зубьями, особенно в массовом производстве.

     Осевая форма III – равновысокие зубья (рис.4.12, в). Образующие конусов делительного, впадин и вершин параллельны. Высота зуба постоянна по всей длине. Применяют для передач с межосевым углом Σ меньше 40° и круговыми зубьями при (z ₁² + z ₂²)^1/2 ≥ 60.

   За расчетное сечение конической передачи принято среднее сечение m.

      Для удобства измерения размеры конических колес принято определять по внешнему торцу е зуба.

Различают внешний окружной модуль m _{t е}, средний окружной модуль m _tm (для прямых зубьев), средний нормальный модуль круговых зубьев m _nm.

      Связь между модулями:

m _{t е} = m _tm / (1 – 0,5 К _be); m _{t е} = m _nm / [(1 – 0,5 К _be)cosβ _m ];

m _nm = m _{t е} (1 – 0,5 К _be) cosβ _m,

где К _be = b / R _e – коэффициент ширины зубчатого венца по внешнему конусному расстоянию; принимают К _be ≤ 0,3. Для большинства передач К _be = 0,285;

β _m – угол наклона зуба в среднем сечении.

36

    Для прямых зубьев стандартным (ГОСТ 9563-60) является модуль m _{t е}. В передачах с круговыми зубьями допускается не округлять модули по стандарту,

 

так как одной и той же зуборезной головкой можно нарезать зубья в определенном интервале модуля за счет наладки резцов в головке. Модуль следует вычислять с точностью 0,0001 мм.

     Диаметры делительных окружностей:

                           d _e = m _{t е} z; d _m = m _tm z = m _nm z / cosβ _m.

     Внешнее конусное расстояние

                                 R _e = [(0,5 d _{e 1})² + (0,5 d _{e 2})²]^1/2 = 0,5 d _{e 1}(1 + u ²)^1/2.

     Ширина зубчатого венца

                                 b = К _be R _e = 0,285∙0,5 d _{e 1}(1 + u ²)^1/2 = 0,143 d _{e 1}(1 + u ²)^1/2.

     Передаточное число

         и = d _{e 2} / d _{e 1} = d _{m 2} / d _{m 1} = z ₂ / z ₁ = 2 R _e sinδ₂ / (2 R _e sinδ₁) = sinδ₂ / sinδ₁.

     При δ₁ + δ₂ = 90^О, где δ – углы делительных конусов, имеем δ₁ = 90^О – δ₂ и тогда  и = tgδ₂. Так же δ₂ = 90^О – δ₁ и и = сtgδ₁.

     Для передачи с круговыми зубьями профили зубьев конических колес в среднем нормальном сечении близки к профилям зубьев эквивалентных цилиндрических прямозубых колес. Приведение к последним осуществляют в два этапа:

1. К эквивалентным цилиндрическим косозубым колесам с углом наклона зубьев β _m;

2. От них к эквивалентным прямозубым цилиндрическим колесам.

     Из-за двойного приведения параметры называютбиэквивалентными:

m _v = m _nm; b _v = b; d _vnm = d _m / (cosδcos²β _m); z _vnm = z / (cosδcos³β _m);

и _v = z _{vnm 2} / z _{vnm 1} = z ₂cosδ₁cos³β _m / (z ₁cosδ₂cos³β _m) = (z ₂ / z ₁)tgδ₂ = u ².

       Для прямых зубьев в приведенных формулах следует принять β _m = 0.

4.6.2. Силы в зацеплении

 

 

	Рис. 4.13

 

 

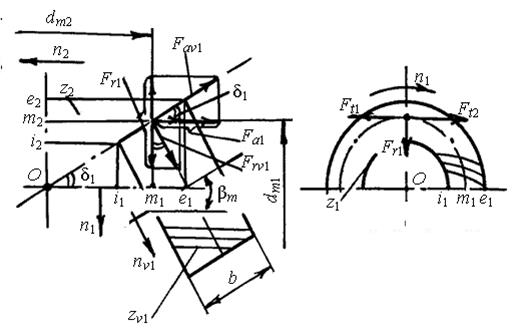
        1. Окружная сила (рис. 4.13) F _t = 2000 Т / d _m.

             

 

         2. Радиальная сила на шестерне F _{r 1}, равная осевой силе на колесе F _{а 2}:

                         F _{r 1} = F _{а 2} = F _t (tgα _n cosδ₁ m sinβ _m sinδ₁) / cosβ _m.               (4.13)

    3. Осевая сила на шестерне F _{а 1}, равная радиальной силе на колесе F _{r 2}:

                         F _{а 1} = F _{r 2} = F _t (tgα _n sinδ₁ ± sinβ _m cosδ₁) / cosβ _m,              (4.14)

где в формулах (4.13) и (4.14) α _n – средний нормальный угол зацепления (α _n ≈

≈ 20°); β _m = 35° – средний угол наклона зуба; δ₁ – угол делительного конуса шестерни.

       Знаки в скобках:

если смотреть с вершины делительного конуса О, то при совпадении вращения и наклона зубьев – верхние знаки, при отсутствии совпадения – нижние.

       Знаки результата:

во избежание заклинивания зубьев при значительных зазорах в подшипниках необходимо обеспечить направление осевой силы F_{а 1} от вершины к внешнему торцу е ₁, т.е. сила F_{а 1} должна быть положительной. Это возможно при совпадении вращения и наклона зубьев.

    4. Нормальная сила в зацеплении F _n = F _t / (cosα _n cosβ _m).

Для прямых зубьев в формулах сил следует положить β _m = 0:

1) F _{t 1} = F _{t 2} = 2000 Т / d _m; 2) F _{r 1} = F _{а 2} = F _t tgα cosδ₁;

3) F _{а 1} = F _{r 2} = F _t tgα sinδ₁; 4) F _n = F _t / cosα.