По формуле тангенс катета прямоугольного сферического треугольника найдем

tg {90 - (X / R)} = tg (90 - j ) cos ( l - L o)

Или

ctg (X / R) = ctg j cos ( l - L o), (113)

где Y / R и X / R - дуги больших кругов - сферические прямоугольные координаты, выраженные в радианах;

X и Y - сферические прямоугольные координаты, выраженные в линейных единицах;

R - радиус Земли.

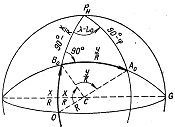
Геометрическое место точек, имеющих одинаковую ординату У, представляет собой малый круг аАоО.1 (рисунок вверху), плоскость которого параллельна плоскости осевого меридиана. Радиус такого малого круга зависит от величины сферической ординаты Y и определяется по формуле r = R cos (Y/R). (114)
Сферический угол PNAoa = g при заданной точке Aо между ее меридианом и малым кругом, плоскость которого параллельна плоскости осевого меридиана, называется углом схождения или сближения меридианов. Величина его зависит от разности долгот между осевым меридианом и меридианом точки Аo и от широты этой точки. Определяется угол сближения меридианов по формуле g = (l - Lo)sin j. (115)

Знак угла сближения меридианов определяется расположением точек относительно осевого меридиана. Для точек, расположенных восточнее осевого меридиана, угол сближения меридианов будет иметь знак плюс; для точек, находящихся западнее осевого
На плоскости проекции сферические прямоугольные координаты X, Y изображаются в виде плоских прямоугольных координат х, у. При этом на проекции образуется сетка, составленная двумя семействами взаимно перпендикулярных параллельных прямых линий. Сферический угол схождения меридианов g в силу равноугольности проекции изображается на проекции плоским углом схождения меридианов g в виде угла между меридианами и линиями y = сonst.

§ 36. Применение карт в проекции Гаусса для навигационных целей

Для навигационных целей наиболее употребительны карты масштаба 1: 100000 и крупнее. При таких масштабах ошибки графической прокладки определений места по сеткам изолиний будут незначительными и карты обеспечат точное вождение корабля по заданной линии пути с осуществлением коррекции курса на основе определений места.
Наиболее часто встречающимися навигационными задачами, решаемыми на карте в проекции Гаусса, являются:

— нанесение точки по заданным координатам или измерение (снятие) координат заданной точки;
— прокладка направлений (пеленгов);
— счисление пути корабля;
— прокладка определений места.

На проекции Гаусса, помимо координатных линий прямоугольной системы координат, прямыми изображаются линии дирекционных направлений, пересекающие километровые линии под постоянным углом a или Т.
Линия кратчайшего расстояния — ортодромия (для шара) — изображается на проекции Гаусса кривой, обращенной выпуклостью от осевого меридиана и составляющей со стягивающей ее хордой небольшой угол d''. Поправка d'' вследствие ее малой величины при решении навигационных задач не учитывается. Иными словами, при решении навигационных задач можно считать, что отрезки ортодромии на карте изображаются прямыми линиями.
Локсодромия на проекции Гаусса изображается кривой, обращенной выпуклостью от полюса. Стягивающая локсодромию хорда — прямая линия на карте — практически совпадает с изображением ортодромии вследствие малости угла d''. При сравнительно небольших плаваниях углы f1 и f2, которые локсодромия составляет со стягивающей ее хордой (рисунок), можно принять равными f1 = f2 = f, а локсодромию можно принять за дугу окружности.

Рисунок позволяет заключить:

Т = ИК - g 1 - f и Т = ИК - g 2 + f 2;

- g 1 - f = - g 2 + f 2,

Откуда

f = (g2 - g1) / 2. (130)

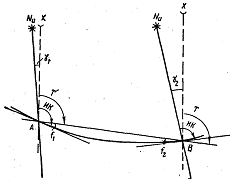
Следовательно, угол, который составляет локсодромия со стягивающей ее хордой, равен полуразности углов сближения меридианов в точках А и В, т. е. в начале и в конце локсодромии.

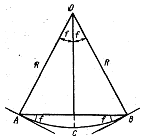
Принимая отрезок локсодромии AСВ за дугу окружности (рисунок), имеющую радиус, равный R, и центр в точке О, можно написать

ÈACB = Sлок = 2Rf;

AB = S орт = 2Rsin f,

откуда

S лок / S орт = f / sin f.

Представив sin f в виде ряда и ограничиваясь по малости f двумя членами разложения, перепишем последнее выражение в виде

S лок / S орт = f / (f - f³ / 6) или S лок / S орт = 1 / (1 - f² / 6),

откуда

S орт = S лок - S лок * (f² / 6).

Обозначив S лок - S орт через Δs, получим Δs = S лок (f² / 6). (131)

Выражая f в минутах дуги, будем окончательно иметь

Δs = S лок (f² / 6) arc 1'. (132)

Расчеты по последней формуле показывают, что при S лок =75 миль в j = 60° ошибка от замены локсодромии стягивающей ее хордой оказывается равной примерно 15 м. Если линию локсодромии длиной до 30 миль заменить отрезком хорды, то ошибка Δs не выйдет за пределы 10 м.

Учитывая сделанные выше выводы, можно следующим образом сформулировать рекомендации по решению отдельных навигационных задач на карте в проекции Гаусса.

1) Нанесение точки на карту по ее географическим координатам может быть сделано так же, как и на карте в проекции Меркатора, пользуясь делениями широты и долготы на ближайших рамках карты. Основанием для этого является то обстоятельство, что меридианы, являющиеся ортодромиями, изображаются на проекции Гаусса практически прямыми линиями; параллели, являющиеся частным случаем локсодромии, в пределах 15—20 см также могут быть приняты за прямые. Кроме того, и меридианы и параллели длиной 15—20 см можно принимать за параллельные между собой прямые.
2) Пеленги на карте прокладываются прямыми линиями. Прокладка пеленга на карте должна производиться относительно меридиана, ближайшего к начальной точке пеленга.
3) При ведении счисления путь корабля прокладывается на карте в виде прямой линии под углом относительно ближайшего к начальной точке пути меридиана, равным ИК ± f. Знак поправки за кривизну локсодромии f на карте в проекции Гаусса находится с помощью чертежа с учетом, что локсодромия на карте обращена выпуклостью от ближайшего полюса. При f £ 0,5° можно на карте прокладывать ИК без исправления поправкой.

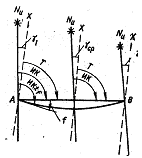
Другой прием прокладки линии пути (курса) состоит в том, что заданное направление движения корабля между двумя точками (ИК) прокладывается относительно меридиана, расположенного примерно посредине между точками A и B без всяких поправок. Линию пути (курса) можно откладывать и относительно вертикальных километровых линий (линии у = const). При этом угол между линией пути (курса) и линией х — дирекционный курс Т — равен

T = ИК - g ср,

Где

g ср = (g 1 + g 2) / 2, g 1 и g 2 — углы сближения меридианов в точках А и В.

4) Пройденное по заданному курсу (пути) расстояние откладывается по прямой без учета поправок за кривизну кратчайших линий и поправки Δs, которые при графической прокладке практически ничтожны.
5) Прокладка определений места на проекции Гаусса ничем практически не отличается от прокладки на карте в проекции Меркатора, если опорные пункты располагаются в пределах рамки карты.

§ 37. Топографические карты, их номенклатура и использование в кораблевождении

Карты, изображающие отдельные участки суши, принято называть топографическими. В отличие от топографических карты, охватывающие целые материки или очень большие участки земной поверхности, называются географическими.
Советские топографические карты масштаба 1: 500000 и крупнее составляются в проекции Гаусса; карта масштаба 1: 1 000 000 составляется как в проекции Гаусса, так и в проекции международной карты мира. Географические карты могут составляться в различных проекциях. Математическая основа топографических карт строится по размерам эллипсоида Красовского в единой системе геодезических координат в шестиградусных зонах. Советские топографические карты составляются по обобщенным инструкциям и наставлениям и могут использоваться всеми ведомствами и учреждениями СССР. Иными словами, топографические карты являются многоцелевыми картами. Рамки топографических карт в виде трапеций образуются линиями картографической сетки меридианов и параллелей. Таким образом, любая топографическая карта представляет собой изображение участка земной поверхности, напоминающего по форме сфероидическую трапецию, ограниченную двумя меридианами и двумя параллелями. Вследствие того что топографические карты строятся, как правило, для шестиградусных зон, масштаб в пределах листа карты сохраняется практически постоянным и равен масштабу, указанному в заголовке карты.
На топографических картах показываются следующие элементы: сооружения на местности, населенные пункты, дорожная сеть, рельеф местности, водные объекты суши, в том числе береговая черта, почвенно-растительный покров, ориентиры, объекты связи.
Для покрытия земной поверхности топографическими картами различных масштабов существует определенная система нарезки (разграфка) карт. В Советском Союзе для всех топографических карт масштаба 1: 1 00000,0 и крупнее до масштаба 1: 10000 включительно принята нарезка карт по меридианам и параллелям.

Размеры сфероидической трапеции, изображаемой на топографических картах различных масштабов

Интервал	1:1 000 000	1:500 000	1:200 000	1:100 000	1:50 000	1:25 000	1:10 000
Δφ	4°	2°	40'	20'	10'	5'	2,5'
Δλ	6°	3°	1°	30'	15'	7,5'	3.75'

Каждый лист карты в зависимости от масштаба имеет свое обозначение. Система условных обозначений буквами и цифрами отдельных листов топографических карт различных масштабов называется номенклатурой карт.
В основу нарезки и номенклатуры топографических карт положен лист карты масштаба 1: 1 000000, охватывающий участок земной поверхности размерами 4° по широте и 6° по долготе. Таким образом, вся земная поверхность делится на колонны — между меридианами и ряды — между параллелями. Каждый ряд сфероидических трапеций имеет разность широт 4°, и каждая колонна имеет разность долгот 6°. Счет рядов ведется от экватора до полюсов, и ряды в северном полушарии обозначаются латинскими буквами А, В, С, D, Е, F и т. д. (рисунок). Территория СССР располагается в пределах рядов I, J, К, L, М, N, О, Р, Q, R, S, Т. Колонны обозначаются арабскими цифрами от 1 до 60; счет их ведется от меридиана 180° к востоку.

Обозначение каждой из карт в масштабе 1: 1000000 слагается из обозначения ряда и колонны. Так, например, миллионная карта, на которой помещен Тбилиси, имеет обозначение К—38.
Нарезка и номенклатура карт масштабов крупнее миллионной осуществляются путем соответствующего деления миллионной карты на более мелкие участки. Так, каждый лист карты масштаба 1:500 000 составляет четверть листа миллионной карты. Для составления карт в масштабе 1:200000 миллионная карта делится на 36 частей, обозначаемых римскими цифрами от I до XXXVI.

Номенклатура карт в масштабе 1:500 000 слагается из обозначения карты масштаба 1: 1 000 000 и соответствующей ей четверти, обозначаемой буквами русского алфавита А, Б, В, Г (например, N—35— Г).

Карты в масштабе 1:200000 обозначаются номером карты масштаба 1: 1 000 000 с добавлением номера соответствующей ее части (например, N—35—XII).

Карты масштаба 1: 100000 получаются делением листа миллионной карты на 144 части, каждая из которых охватывает/ район, ограниченный разностью параллелей Δφ = 20' и по долготе Δλ = 30'. Номенклатура стотысячной карты составляется из обозначения карты масштаба 1:1000000 и номера соответствующей трапеции (например, N—35—24).

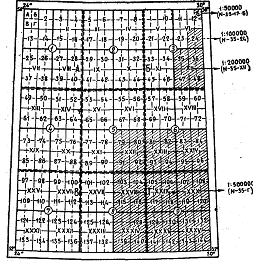
При составлении карт в масштабе 1:50000 лист карты в масштабе 1: 100 000 разбивается на четыре части, каждая из которых обозначается буквами русского алфавита А, Б, В, Г. Обозначаются карты масштаба 1: 50 000 номенклатурой карты масштаба 1: 100 000 с добавлением одной из указанных букв (например,

N - 35 — 12 — Б).