Понятие о построении картографической сетки проекции Меркатора

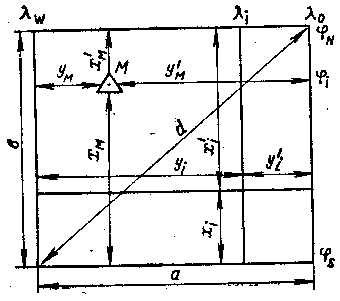
При вычислении картографической сетки проекции Меркатора обычно задают:

— крайние параллели jN, js и меридианы lost, lw изображаемого участка земной поверхности;

— главный масштаб mо карты;

— широту главной параллели jо.

При заданных границах изображаемого участка и главном масштабе вычисление картографической сетки и отрезков меридиана и параллели для нанесения опорных пунктов сводится к расчету:

— длины нижней (верхней) рамки а;

— длины боковой рамки b;

— диагонали рамки d;

— отрезков боковой рамки для нанесения промежуточных параллелей х(х');

— отрезков нижней (верхней) рамки для нанесения промежуточных меридианов у (у').

Для вычисления размеров рамки карты и построения картографической сетки используется так называемая единица карты е (мм), являющаяся для данной карты величиной постоянной.

Единица карты представляет собой длину одной минуты экватора или параллели на карте, выраженную в миллиметрах. Длина одной минуты экватора эллипсоида равна а аrс 1', следовательно, в заданном масштабе единица карты выражается формулой

e = a arc 1' / Cэ = Рэ / Сэ, (103)

Где Рэ—длина 1' дуги параллели.

Для главной параллели (jo, Со) единица карты выражается формулой

e = r o arc 1' / C o = P o / Co, (104)

А для любой другой параллели j формулой

e = rj arc 1' / Cj. (105)

Таким образом, для единицы карты е можно написать ее значения

e = a arc 1' / Cэ = Рэ / Сэ = ro arc 1' / Co = Po = Pj / Cj = const. (106)

Поскольку для рассчитываемой рамки карты задаются главная параллель jo и масштаб mо по главной параллели, то единицу карты вычисляют по формуле

e = Po / Co = ro arc 1' / Co,

где ro = No cos jo должно быть выражено в мм. Для стандартных масштабов величины единицы карты е приводятся в табл. 4 Картографических таблиц.

После того как вычислена или выбрана из таблицы единица карты, размеры горизонтальной и вертикальной рамок карты рассчитываются по следующим формулам:

a = e (lo - lw)'

b = e (D N - D s)', (107)

Где (DN - Ds) — разность меридиональных частей крайних северной и южной параллелей изображаемого участка.

Для контроля правильности расчета рамок карты вычисляется ее диагональ d по формуле

d = Ö(a² + b²) (108)

Для проведения меридианов через заданные интервалы Δl долгот картографической сетки рассчитываются удаления их (в миллиметрах) от крайнего западного и для контроля — от крайнего восточного меридианов рамки. Расчет производится по формулам:

yi = e (li - lw)

y' i = e (l o - l i) (109)

Где yi — удаление заданного меридиана с долготой li от крайнего западного меридиана рамки;

Y'i — удаление того же меридиана от крайнего восточного меридиана рамки.

Соблюдение равенства yi + y'i = а служит контролем правильности произведенных вычислений.

Для нанесения промежуточных параллелей вычисляются удаления этих параллелей xi и x'i от крайних (северной и южной) параллелей рамки. Расчет производится по формулам:

xi = e (Di - Ds)'

x'i = e (DN - Di), (110)

Где Di — меридиональная часть заданной промежуточной параллели.

Ошибки вычислений элементов картографической сетки не должны превышать ошибок графических построений, т. е. 0,2 мм.

Промежуточные меридианы сетки могут проводиться сколь угодно часто, однако в действительности они проводятся через интервалы долгот, кратные 5' или 10', на расстояниях один от другого 150—200 мм. Разбивка широтной и долготной шкал рамки карты производится путем деления отрезков рамки карты между проведенными меридианами и параллелями на равные части.

На рассчитанную и построенную картографическую сетку наносятся опорные пункты и другие подробности (береговая черта, результаты промера и другая обстановка) местности, охватываемой данной картой. Опорные пункты наносятся на сетку по их географическим координатам. Практически нанесение опорных пунктов сводится к вычислению отстояния меридиана и параллели опорного пункта от рамок карты. Расчетными формулами при этом являются:

xM = e(DM - Ds)'

x' M = e(D N - D M)'

y M = e(l M - l w)'

y' M = e(l o - l M)', (111)

Где