Тренировочная работа 12 (к задачам Д1.15—Д1.18)

Т12.1. На рисунке показана схема лесных дорожек. Пешеход     Т12.1

идет из точки S по дорожкам, на каждой развилке выбирая дорожку случайным образом и не возвращаясь обратно. Най- дите вероятность того, что он попадет в точку F.

Рисунок к задачам Т12.1 и Т12.2

Т12.2. На рисунке показана схема лесных дорожек. Пешеход     Т12.2

идет из точки S по дорожкам, на каждой развилке выбирая дорожку случайным образом и не возвращаясь обратно. Най- дите вероятность того, что он попадет в грибное место, обо- значенное на схеме закрашенной областью.

Т12.3. На рисунке изображен лабиринт. Жук вползает в лаби-     Т12.3

ринт в точке «Вход». Развернуться или ползти назад жук не может, поэтому на каждом разветвлении жук выбирает один из путей, по которым он еще не полз. Считая, что выбор чи- сто случайный, определите, с какой вероятностью жук придет к одному из выходов.

 

Ответы:                                                           Тренировочная работа 12

Т12.4

Т12.5

Т12.6

Т12.7

Т12.4. В ветеринарной лаборатории проводятся анализы на пироплазмоз. Если анализ не выявляет заболевания, гово- рят, что результат анализа отрицательный, в противном слу- чае — что результат положительный. Если анализ отрица- тельный, врач назначает повторный анализ. Третий анализ не назначается. Вероятность ложного положительного результа- та у здоровой собаки равна 0, 005. Найдите вероятность того, что с помощью такой процедуры у здоровой собаки будет ошибочно диагностирован пироплазмоз. Результат округлите до сотых.

Т12.5. При артиллерийской стрельбе автоматическая систе- ма делает выстрел по цели. Если цель не уничтожена, то си- стема делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уни- чтожения некоторой цели при первом выстреле равна 0, 6, а при каждом следующем — 0, 8. Сколько выстрелов потребует- ся для того, чтобы вероятность уничтожения цели была не менее чем 0, 99.

Т12.6. Всем пациентам с подозрением на гепатит делают ана- лиз крови. Если анализ выявляет гепатит, то результат анали- за называется положительным. У больных гепатитом пациен- тов анализ дает положительный результат с вероятностью 0, 9. Если пациент не болен гепатитом, то анализ может дать лож- ный положительный результат с вероятностью 0, 01. Извест- но, что у 6 % пациентов с подозрением на гепатит анализ дает положительный результат. Найдите вероятность того, что па- циент, поступивший с подозрением на гепатит, действитель- но болен гепатитом. Ответ округлите до тысячных.

Т12.7. В Волшебной стране бывает два типа погоды: хорошая и замечательная, причем погода держится неизменной весь день. Известно, что с вероятностью 0, 8 погода завтра будет такая же, как сегодня. Сегодня 3 июля, и погода в Волшебной стране замечательная. Найдите вероятность того, что 5 июля погода в Волшебной стране также будет замечательная.

 

Образец написания:

Диагностическая работа 2

Д2.1. В прямоугольном треугольнике случайно выбирается     Д2.1

вершина. Найдите вероятность того, что выбрана вершина прямого угла.

 

Д2.2. Игральный кубик бросили один раз. Какова вероят-      Д2.2

ность того, что выпало число, меньшее чем 3?

 

 

Д2.3. На столе лежат 10 карточек, на которых написаны числа      Д2.3 от 1 до 10. Миша случайно вытягивает одну карточку. С какой вероятностью число на выбранной карточке является состав-

ным?

 

Д2.4. В случайном эксперименте бросают две игральные ко- Д2.4

сти. Найдите вероятность того, что в сумме выпадет 7 очков.

 

 

Д2.5. В случайном эксперименте монету бросили три раза. Д2.5

Какова вероятность выпадения комбинации ООР?

 

 

Д2.6. В соревнованиях по метанию копья участвуют 6 спортс- Д2.6

менов из Польши, 5 спортсменов из Чехии, 8 спортсменов из Австрии и 6 — из Германии. Порядок, в котором выступа- ют спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступивший последним, окажется из Австрии.

Д2.7. В среднем из 1000 зарядных устройств, поступивших       Д2.7

в продажу, 12 неисправны. Найдите вероятность того, что одно случайно выбранное зарядное устройство окажется ис- правным.

 

Д2.8. В чемпионате по гимнастике участвуют 25 спортсме-       Д2.8

нок: 7 из Эстонии, 4 из Латвии, остальные — из Литвы. Поря- док, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Литвы.

Ответы:

Ответы:                                                         Диагностическая работа 2

Д2.9

 

Д2.10

 

Д2.11

 

Д2.12

 

Д2.13

 

Д2.14

 

Образец написания:

Д2.9. В избирательный список внесены имена трех кандида- тов: А., Б. и В. Порядок их в списке определяется случайно с помощью компьютера. Найдите вероятность того, что их имена будут расположены в списке в алфавитном порядке. Результат округлите до сотых.

 

Д2.10. Системный администратор обслуживает два сервера. Вероятность того, что в течение дня первый сервер потребу- ет вмешательства, равна 0, 2. Вероятность того, что второй сервер потребует вмешательства, равна 0, 15. Найдите веро- ятность того, что в течение дня ни один из серверов не потре- бует вмешательства.

 

Д2.11. Вероятность того, что на тесте по обществознанию уча- щийся П. верно ответит больше чем на 10 вопросов, равна 0, 39. Вероятность того, что П. верно ответит больше чем на 9 вопросов, равна 0, 44. Найдите вероятность того, что П. вер- но ответит ровно на 10 вопросов.

 

Д2.12. При артиллерийской стрельбе автоматическая систе- ма делает выстрел по цели. Если цель не уничтожена, то си- стема делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уни- чтожения некоторой цели при первом выстреле равна 0, 4, а при каждом следующем — 0, 6. Сколько выстрелов потребу- ется для того, чтобы вероятность уничтожения цели была не менее чем 0, 98?

 

Д2.13. Вероятность того, что новый принтер в течение года поступит в гарантийный ремонт, равна 0, 055. В некотором го- роде из 1000 проданных принтеров в течение года в гарантий- ную мастерскую поступило 53 штуки. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?

 

Д2.14. Из районного центра в деревню ежедневно ходит ав- тобус. Вероятность того, что в пятницу в автобусе окажется меньше 35 пассажиров, равна 0, 84. Вероятность того, что ока- жется меньше 25 пассажиров, равна 0, 48. Найдите вероят- ность того, что число пассажиров будет от 25 до 34.

Диагностическая работа 2                                                                Ответы:

 

Д2.15. Бревно плывет по течению реки к устью. Река разделяет-    Д2.15

ся на рукава. При каждом разветвлении реки бревно с равны- ми шансами может попасть в любой из образующихся рукавов. Найдите вероятность того, что бревно попадет в точку S.

Д2.16. Бревно плывет по течению реки к устью. Река разделя-      Д2.16

ется на рукава. При каждом разветвлении реки бревно с рав- ными шансами может попасть в любой из образующихся ру- кавов. Некоторые рукава около выхода в море перегорожены сетями (см. рисунок). Найдите вероятность того, что бревно попадет в какую-нибудь сеть.

Ответы:                                                         Диагностическая работа 2

Д2.17

Д2.18

Д2.17. Лампы определенного типа выпускают только два заво- да. Первый завод выпускает 40 % ламп, второй — 60 %. Среди продукции первого завода 2 % бракованных ламп, среди про- дукции второго — 3 %. Найдите вероятность того, что случай- но купленная в магазине лампа этого типа окажется исправ- ной.

 

Д2.18. Лампы определенного типа выпускают только два заво- да. Среди продукции первого завода 2 % бракованных ламп, среди продукции второго — 3 %. Известно, что при случайном выборе вероятность купить неисправную лампу этого типа равна 0, 024. Найдите вероятность того, что случайно выбран- ная лампа произведена на первом заводе.

 

Диагностическая работа 3

Д3.1. В кармане у Миши было четыре конфеты — «Грильяж»,       Д3.1

«Белочка», «Коровка» и «Ласточка», а также ключи от квар- тиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась кон- фета «Грильяж».

Д3.2. Игральный кубик бросили один раз. Какова вероят- Д3.2

ность того, что выпало число, кратное 2?

Д3.3. На столе лежат 10 карточек, на которых написаны числа

Ответы:

от 1 до 10. Дима случайно вытягивает одну карточку. С какой вероятностью число на выбранной карточке кратно 3?

Д3.4. В случайном эксперименте бросают две игральные ко- сти. Найдите вероятность того, что сумма выпавших очков нечетна.

Д3.5. В случайном эксперименте монету бросили три раза. Найдите вероятность того, что при втором броске монете вы- пал орел.

Д3.6. В соревнованиях по толканию ядра участвуют 10 спортс- менов из России, 4 спортсмена из Белоруссии, 8 спортсменов из Казахстана и 3 — из Украины. Порядок, в котором выступа- ют спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Казахстана.

Д3.3

Д3.4

Д3.5

Д3.6

Д3.7. В среднем из 1000 карт памяти, поступивших в продажу,      Д3.7 7 неисправны. Найдите вероятность того, что одна случайно выбранная при покупке карта памяти окажется исправной.

Д3.8. В чемпионате по гимнастике участвуют 20 спортсме-       Д3.8

нок: 5 из России, 9 из Молдовы, остальные — из Украины. По-

рядок, в котором выступают гимнастки, определяется жреби- ем. Найдите вероятность того, что гимнастка, выступающая первой, окажется из Украины.

Д3.9. Механические часы с двенадцатичасовым циферблатом      Д3.9 в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув от-

метки 11 часов, но не дойдя до отметки 1 час.

Ответы:                                                         Диагностическая работа 3

Д3.10

Д3.11

Д3.12

Д3.13

Д3.14

Д3.15

Д3.10. В фирме такси есть два микроавтобуса. Каждый из них в случайный момент времени свободен с вероятностью 0, 55. Какова вероятность того, что в случайный момент ни один автобус не будет свободен?

Д3.11. Вероятность того, что новая электрическая мясорубка прослужит больше года, равна 0, 96. Вероятность того, что она прослужит больше двух лет, равна 0, 91. Найдите вероятность того, что мясорубка прослужит меньше двух лет, но больше года.

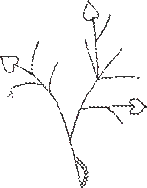
Д3.12. Вероятность того, что батарейка бракованная, равна 0, 06. Покупатель в магазине выбирает случайную упаковку, в которой две такие батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.

Д3.13. Биатлонист пять раз стреляет по мишеням. Вероят- ность попадания в мишень при одном выстреле равна 0, 7. Найдите вероятность того, что биатлонист первые четыре ра- за попал в мишени, а последний раз промахнулся. Результат округлите до сотых.

Д3.14. В магазине стоят три платежных автомата. Каждый из них может быть неисправен с вероятностью 0, 1. Найдите вероятность того, что хотя бы один автомат исправен.

Д3.15. Гусеница ползет вверх по ветви куста (см. рисунок). На каждом разветвлении гусеница с равными шансами может попасть на любую из растущих веточек. Какова вероятность того, что гусеница попадет в точку A?

Диагностическая работа 3                                                                Ответы:

 

Д3.16. Гусеница ползет вверх по ветви куста. На каждой раз-      Д3.16

вилке гусеница с равными шансами может попасть на любую из растущих веточек. Найдите вероятность того, что гусеница доберется до одного из листьев.

 

Д3.17. Автоматическая линия изготавливает батарейки. Веро-      Д3.17

ятность того, что готовая батарейка неисправна, равна 0, 02. Перед упаковкой каждая батарейка проходит систему контро- ля. Вероятность того, что система забракует неисправную ба- тарейку, равна 0, 99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0, 01. Найдите вероят- ность того, что случайно выбранная батарейка будет забрако- вана.

 

Д3.18. Чтобы пройти в следующий круг  соревнований, фут-      Д3.18

больной команде нужно набрать 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность то- го, что команде не удастся выйти в следующий круг соревно- ваний. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы, а вероятность ничьей равна 0, 1. Ре- зультат округлите до сотых.

 

Д4.1

Д4.2

Ответы:

 

Диагностическая работа 4

Д4.1. Саша и Миша решили поиграть в шахматы. Саша прячет в одной руке белую пешку, а в другой — черную. Миша выби- рает цвет своих фигур, указывая на левую или правую руку Саши. С какой вероятностью Миша укажет на руку с белой пешкой?

Д4.2. Игральную кость бросили один раз. Какова вероятность того, что выпало простое число?

Д4.3. На столе лежат 10 карточек, на которых написаны числа

Д4.3                                 от 1 до 10. Даша случайно вытягивает одну карточку. С какой вероятностью число на выбранной карточке больше 7?

Д4.4. В случайном эксперименте бросают две игральные ко-

Д4.4                                 сти по очереди. Найдите вероятность того, что на первой ко- сти выпало больше очков, чем на второй.

Д4.5. В случайном эксперименте монету бросили три раза. Найдите вероятность того, что решка выпала не более двух

Д4.5

Д4.6

Д4.7

Д4.8

Д4.9

раз.

Д4.6. В соревнованиях по толканию ядра участвуют 4 спортс- мена из Эстонии, 3 спортсмена из Латвии, 5 спортсменов из Литвы и 8 — из Дании. Порядок, в котором выступают спортс- мены, определяется жребием. Найдите вероятность того, что спортсмен, выступивший последним, окажется из Латвии.

Д4.7. В среднем из 1000 телевизоров, поступивших в прода- жу, 3 неисправны. Найдите вероятность того, что случайно выбранный телевизор при проверке окажется исправным.

Д4.8. В чемпионате по гимнастике участвуют 20 спортсме- нок: 7 из Канады, 6 из США, остальные — из Великобрита- нии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что гимнастка, которая выступает первой, окажется из Великобритании.

Д4.9. Аня и Таня выбирают по одному натуральному числу от 1 до 9 независимо друг от друга. Найдите вероятность того, что сумма этих чисел делится на 3.

Диагностическая работа 4                                                                Ответы:

 

Д4.10. Автоматическая линия разливает питьевую воду в бу-      Д4.10

тылки по 5 л. В 98 % случаев объем воды в бутылке отличается от нормы не больше чем на 0, 2 л. Какова вероятность того, что в случайно выбранной бутылке объем воды будет меньше чем 4, 8 л или больше чем 5, 2 л?

Д4.11. На зачете по тригонометрии школьнику достается одна       Д4.11

задача из сборника. Вероятность того, что это задача на тему

«Формулы приведения», равна 0, 24. Вероятность того, что это задача на тему «Универсальная тригонометрическая подста- новка», равна 0, 08. В сборнике нет задач, которые одновре- менно относятся к этим двум темам. Найдите вероятность того, что на зачете школьнику достанется задача по одной из этих двух тем.

Д4.12. В интернет-магазине три телефонных оператора. В слу-     Д4.12 чайный момент оператор занят разговором с клиентом с ве- роятностью 0, 6 независимо от других. Клиент звонит в мага-

зин. Найдите вероятность того, что в этот момент все опера- торы заняты.

Д4.13. Игральный кубик бросают три раза. Какова вероят-      Д4.13

ность того, что все три раза выпадут четные числа?

Д4.14. Вероятность того, что новый маркер пишет плохо (или

не пишет), равна 0, 06. Покупатель в магазине выбирает один такой маркер. Найдите вероятность того, что этот маркер пи- шет хорошо.

Д4.14

Д4.15. Капля воды стекает по металлической сетке (см. рису-     Д4.15

нок). В каждом узле сетки капля с равными шансами может

стечь вниз вправо или влево. Найдите вероятность того, что, скатившись вниз, капля окажется в точке A.

Рисунок к задачам Д4.15 и Д4.16

Ответы:                                                         Диагностическая работа 4

Д4.16

Д4.17

Д4.18

Д4.16. Капля воды стекает по металлической сетке (см. ри- сунок на предыдущей странице). В каждом узле сетки капля с равными шансами может стечь вниз вправо или влево. Най- дите вероятность того, что, скатившись вниз, капля окажется на участке A — B.

Д4.17. Ковбой Джон попадает в муху на стене с вероятностью 0, 9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0, 2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене му- ху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнется.

Д4.18. В ветеринарной лаборатории проводятся анализы на лямблиоз ¹. Если анализ не показывает заболевания, гово- рят, что результат анализа отрицательный, в противном слу- чае — что результат положительный. Вероятность ложного отрицательного анализа у больной лямблиозом собаки равна 0, 6. Если анализ отрицательный, врач назначает повторный анализ. Третий анализ не назначается. Найдите вероятность того, что с помощью такой процедуры у больной лямблиозом собаки удастся выявить это заболевание.

 

Образец написания:

1 Кишечное заболевание, которое вызывается простейшими организма- ми — лямблиями.

Справочные материалы

Элементарные события (элементарные исходы) опыта — простейшие события, которыми может окончиться случайный опыт. Сумма вероятностей всех элементар- ных событий опыта равна 1.

Вероятность события A равна сумме вероятностей элементарных событий, благо- приятствующих этому событию.

Объединение событий A ∪ B — событие, состоящее из элементарных исходов,

благоприятствующих хотя бы одному из событий A, B.

Пересечение событий A ∩ B — событие, состоящие из элементарных исходов, бла- гоприятствующих обоим событиям A и B.

П р о т и в о п о л о ж н о е с о б ы т и е. Событие A ¯¯, состоящее из тех и только тех элементар- ных исходов опыта, которые не входят в A, называется противоположным событию A. Несовместные события — события, которые не наступают в одном опыте. Напри-

мер, противоположные события несовместны.

Вероятности противоположных событий:

P(A)+ P(A ¯) = 1;   P(A ¯¯) = 1 − P(A).

Формула сложения вероятностей:

P(A ∪ B) = P(A)+ P(B) − P(A ∩ B).

Формула сложения вероятностей для несовместных событий:

P(A ∪ B) = P(A)+ P(B).

Формула умножения вероятностей:

P(A ∩ B) = P(A)· P(B | A),

где P(B | A) — условная вероятность события B при условии, что событие A наступило.

Независимые события. События A и B называются независимыми, если

P(A ∩ B) = P(A)· P(B).

Формула вероятности k успехов в серии из n испытаний Бернулли:

n

C k p k q n − k,

где C^k = n!

— число сочетаний, p — вероятность успеха, q = 1 − p — вероятность

n    k!(n − k)!

неудачи в одном испытании.

Ответы

Диагностическая работа 1

Д1.1. 0, 25. Д1.2. 1. Д1.3. 0, 5. Д1.4. 5. Д1.5. 0, 375. Д1.6. 0, 36. Д1.7. 0, 994. Д1.8. 0, 25.

3                                 36

Д1.9. 0, 25. Д1.10. 0, 9. Д1.11. 0, 35. Д1.12. 0, 52. Д1.13. 0, 02. Д1.14. 0, 9975. Д1.15. 0, 125.

Д1.16. 5. Д1.17. 0, 0135. Д1.18. 0, 75.

12

Тренировочная работа 1

Т1.1. 0, 5. Т1.2. 0, 5. Т1.3. 0, 5. Т1.4. 0, 3. Т1.5. 0, 4. Т1.6. 0, 5. Т1.7. 6. Т1.8. 1. Т1.9. 0, 375.

3

2            1             2

Т1.10. 3. Т1.11. 3. Т1.12. 3.

 

 

Тренировочная работа 2

Т2.1. 0, 5. Т2.2. 0, 5. Т2.3. 1. Т2.4. 1. Т2.5. 1. Т2.6. 4. Т2.7. 5. Т2.8. 0, 5. Т2.9. 7.

3            6            6                               36

Т2.10. 1. Т2.11. 1. Т2.12. 1. Т2.13. 19.   Т2.14. 19.

6             12             9                                   36

Тренировочная работа 3

Т3.1. 0, 25. Т3.2. 0, 5. Т3.3. 0, 75. Т3.4. 0, 125. Т3.5. 0, 375. Т3.6. 0, 125.   Т3.7. 0, 5.

Т3.8.   0, 5.   Т3.9.   0, 5.   Т3.10.   0, 5.   Т3.11.   Одинаково  вероятно.   Т3.12.   16.   Т3.13.   0, 25.

Т3.14. 0, 3125.

 

Тренировочная работа 4

Т4.1. 0, 25. Т4.2. 2. Т4.3. 5. Т4.4. 3. Т4.5. 0, 125. Т4.6. 0, 33. Т4.7. 0, 14. Т4.8. 0, 375.

3            6

Т4.9. 0, 125. Т4.10. 0, 3125. Т4.11. 1. Т4.12. 0, 5. Т4.13. 18. Т4.14. 4. Т4.15. 0, 125.

3                                                         9

Тренировочная работа 5

Т5.1. 0, 125. Т5.2. 0, 35. Т5.3. 5. Т5.4. 1. Т5.5. 0, 498. Т5.6. 0, 1. Т5.7. 100. Т5.8. 0, 995.

6            6                                                          109

Т5.9. 0, 97. Т5.10. 0, 2. Т5.11. 1. Т5.12. 0, 48. Т5.13. 0, 3.

21

Тренировочная работа 6

Т6.1. 1. Т6.2. 15. Т6.3. 0, 45. Т6.4. 0, 504. Т6.5. 1. Т6.6. 1. Т6.7. 0, 993. Т6.8. 0, 972.

9            32                                                              6            3

Т6.9. 100. Т6.10. 800. Т6.11. 1. Т6.12. 14. Т6.13. 0, 25.

103

1017

111             27

Тренировочная работа 7

Т7.1. 0, 2. Т7.2. 0, 3. Т7.3. 0, 2. Т7.4. 0, 985. Т7.5. 1. Т7.6. 25. Т7.7. 0, 996. Т7.8. 0, 966.

3            27

Т7.9. 0, 7. Т7.10. 153. Т7.11. 2. Т7.12. 0, 7. Т7.13. 20. Т7.14. 28.

953

333

81             225

Ответы

Тренировочная работа 8

Т8.1. 0, 81. Т8.2. 0, 006. Т8.3. 0, 035. Т8.4. 0, 19. Т8.5. 0, 64. Т8.6. 0, 07. Т8.7. 0, 24.

Т8.8. 0, 37. Т8.9. 0, 98. Т8.10. 3. Т8.11. 0, 33. Т8.12. 625. Т8.13. 0, 24. Т8.14. 0, 7056.

1296

 

Тренировочная работа 9

Т9.1. 0, 9025. Т9.2. 0, 006. Т9.3. 0, 02. Т9.4. 0, 98. Т9.5. 45. Т9.6. 0, 08. Т9.7. 0, 32.

46

Т9.8. 0, 19. Т9.9. 0, 027. Т9.10. 0, 04. Т9.11. 0, 02. Т9.12. 0, 343. Т9.13. 0, 0243. Т9.14. 0, 875.

 

Тренировочная работа 10

Т10.1. 0, 004. Т10.2. 0, 03. Т10.3. 0, 036. Т10.4. 0, 03. Т10.5. 0, 38. Т10.6. 0, 06.   Т10.7. 0, 08.

Т10.8. 0, 23. Т10.9. 0, 56. Т10.10. 0, 3249. Т10.11. 0, 992. Т10.12. 0, 999. Т10.13.   0, 91.

Т10.14. 0, 096.

 

 

 

1              17

Тренировочная работа 11

1

Т11.1. 12. Т11.2. 36. Т11.3. 24. Т11.4. 0, 91. Т11.5. 0, 392. Т11.6. 0, 32. Т11.7. 0, 0545.

Тренировочная работа 12

Т12.1. 1. Т12.2. 13. Т12.3. 1. Т12.4. 0, 01. Т12.5. 4. Т12.6. 0, 056. Т12.7. 0, 68.

9             36             6

 

Диагностическая работа 2

Д2.1. 1. Д2.2. 1. Д2.3. 0, 5. Д2.4. 1. Д2.5. 0, 125. Д2.6. 0, 32. Д2.7. 0, 988. Д2.8. 0, 56.

3             3                                  6

Д2.9. 0, 17. Д2.10. 0, 68. Д2.11. 0, 05. Д2.12. 5. Д2.13. 0, 002. Д2.14. 0, 36. Д2.15. 1.

12

Д2.16. 0, 375. Д2.17. 0, 974. Д2.18. 0, 6.

 

Диагностическая работа 3

Д3.1. 0, 25. Д3.2. 0, 5. Д3.3. 0, 3. Д3.4. 0, 5. Д3.5. 0, 5. Д3.6. 0, 32. Д3.7. 0, 993. Д3.8. 0, 3.

Д3.9. 1. Д3.10. 0, 2025. Д3.11. 0, 05. Д3.12. 0, 8836. Д3.13. 0, 07. Д3.14. 0, 999. Д3.15. 0, 125.

6

1

Д3.16. 6. Д3.17. 0, 0296. Д3.18. 0, 71.

Диагностическая работа 4

Д4.1. 0, 5. Д4.2. 0, 5. Д4.3. 0, 3. Д4.4. 5. Д4.5. 0, 875. Д4.6. 0, 15. Д4.7. 0, 997. Д4.8. 0, 35.

12

Д4.9. 1. Д4.10. 0, 02. Д4.11. 0, 32. Д4.12. 0, 216. Д4.13. 0, 125. Д4.14. 0, 94. Д4.15. 0, 25.

3

Д4.16. 0, 875. Д4.17. 0, 52. Д4.18. 0, 64.

Содержание

От редактора серии................................................................................................... 3

Введение................................................................................................................... 4

Диагностическая работа 1.......................................................................................... 6

Решения задач диагностической работы 1............................................................... 10

Тренировочная работа 1 (к задаче Д1.1).................................................................. 22

Тренировочная работа 2 (к задачам Д1.2, Д1.4)....................................................... 24

Тренировочная работа 3 (к задачам Д1.3, Д1.5)....................................................... 26

Тренировочная работа 4 (к задачам Д1.1—Д1.5)...................................................... 28

Тренировочная работа 5 (к задачам Д1.6—Д1.9)...................................................... 30

Тренировочная работа 6 (к задачам Д1.6—Д1.9)...................................................... 32

Тренировочная работа 7 (к задачам Д1.6—Д1.9)...................................................... 34

Тренировочная работа 8 (к задачам Д1.10—Д1.14)................................................... 36

Тренировочная работа 9 (к задачам Д1.10—Д1.14)................................................... 39

Тренировочная работа 10 (к задачам Д1.10—Д1.14)................................................. 41

Тренировочная работа 11 (к задачам Д1.15—Д1.18)................................................. 43

Тренировочная работа 12 (к задачам Д1.15—Д1.18)................................................. 45

Диагностическая работа 2........................................................................................ 47

Диагностическая работа 3........................................................................................ 51

Диагностическая работа 4........................................................................................ 54

Справочные материалы.......................................................................................... 57

Ответы..................................................................................................................... 58

 

 

 

Учебно-методическое пособие

Иван Ростиславович Высоцкий Иван Валериевич Ященко

ЕГЭ 2019. МАТЕМАТИКА. ТЕОРИЯ ВЕРОЯТНОСТЕЙ.

ЗАДАЧА 4 (ПРОФИЛЬНЫЙ УРОВЕНЬ). ЗАДАЧА 10 (БАЗОВЫЙ УРОВЕНЬ). РАБОЧАЯ ТЕТРАДЬ

Под редакцией И. В. Ященко

Подписано в печать 07.08.2018 г. Формат 70 × 90 ¹/₁₆. Бумага офсетная.

Печать офсетная. Печ. л. 4. Тираж 3000 экз. Заказ №.

Издательство Московского центра непрерывного математического образования.

119002, Москва, Большой Власьевский пер., д. 11. Тел. [phone].

Отпечатано в полном соответствии с качеством предоставленного электронного оригинал-макета в ОOО «Ярославский полиграфический комбинат».

150049, Ярославль, ул. Свободы, 97.

Книги издательства МЦНМО можно приобрести в магазине «Математическая книга», Москва, Большой Власьевский пер., д. 11. Тел. [phone]. E-mail: [e-mail]