
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Блок 2. Простейшие правила и формулы вычисления вероятностей
Д1.10. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0, 1. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо. Решение. Определим событие A = {выбранная ручка пишет хорошо}. Известна ве- роятность противоположного события: P(A ¯¯) = 0, 1. Используем формулу вероятности противоположного события: P(A) = 1 − P(A ¯¯) = 1 − 0, 1 = 0, 9. Ответ: 0, 9. Д1.11. На экзамене по геометрии школьнику достается один вопрос из списка экза- менационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окруж- ность», равна 0, 2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0, 15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. Решение. Определим события: A = {вопрос на тему «Вписанная окружность»}, B = {вопрос на тему «Параллелограмм»}. Решения задач диагностической работы 1 События A и B несовместны, так как по условию в списке нет вопросов, относящих- ся к этим двум темам одновременно. Событие C = {вопрос по одной из этих двух тем} является их объединением: C = A ∪ B. Применим формулу сложения вероятностей несовместных событий: P(C) = P(A)+ P(B) = 0, 2 + 0, 15 = 0, 35. Ответ: 0, 35. Д1.12. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0, 3. Вероятность того, что кофе закончится в обоих автоматах, равна 0, 12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах. Решение. Определим события A = {кофе закончится в первом автомате}, B = {кофе закончится во втором автомате}. По условию задачи P(A)= P(B)= 0, 3 и P(A ∩ B)= 0, 12. По формуле сложения вероятностей найдем вероятность события A ∪ B = {кофе закончится хотя бы в одном из автоматов}: P(A ∪ B) = P(A)+ P(B) − P(A ∩ B) = 0, 3 + 0, 3 − 0, 12 = 0, 48. Следовательно, вероятность противоположного события «кофе останется в обоих автоматах» равна
Ответ: 0, 52. 1 − 0, 48 = 0, 52. Д1.13. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0, 8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых. Решение. В этой задаче предполагается, что результат каждого следующего вы- стрела не зависит от предыдущих. Поэтому события «попал при первом выстреле»,
«попал при втором выстреле» и т. д. независимы. Вероятность каждого попадания равна 0, 8. Значит, вероятность каждого промаха равна 1 − 0, 8 = 0, 2. Воспользуемся формулой умножения вероятностей независимых событий. Получаем, что последова- тельность A = {попал, попал, попал, промахнулся, промахнулся} имеет вероятность P(A) = 0, 8 · 0, 8 · 0, 8 · 0, 2 · 0, 2 = 0, 83 · 0, 22 = 0, 512 · 0, 04 = 0, 02048 ≈ 0, 02. Ответ: 0, 02. Решения задач диагностической работы 1 Д1.14. В магазине стоят два платежных автомата. Каждый из них может быть неис- правен с вероятностью 0, 05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен. Решение. В этой задаче также предполагается независимость работы автоматов. Найдем вероятность противоположного события A ¯¯ = {оба автомата неисправны}. Для этого используем формулу умножения вероятностей независимых событий: P(A ¯¯) = 0, 05 · 0, 05 = 0, 0025. Значит, вероятность события A = {хотя бы один автомат исправен} равна P(A)= 1 − P(A ¯¯) = 1 − 0, 0025 = 0, 9975. Ответ: 0, 9975. Примечание. Задачу можно решить с помощью формулы сложения вероятностей несовместных событий. Если вероятности исправности первого и второго автомата назвать соответственно p 1 и p 2, а вероятности того, что они неисправны, — соответ- ственно q 1 и q 2, то P(A) = p 1 p 2 + p 1 q 2 + q 1 p 2. Первое слагаемое соответствует случаю, когда исправны оба, второе — случаю, ко- гда исправен только первый, а третье — случаю, когда исправен только второй. По условию q 1 = q 2 = 0, 05, значит, p 1 = p 2 = 1 − 0, 05 = 0, 95. Тогда P(A) = 0, 952 + 0, 95 · 0, 05 + 0, 05 · 0, 95 = 0, 95 · (0, 95 + 2 · 0, 05) = 0, 9975. Еще более короткий путь дает равенство P(A) = p 1 + q 1 p 2. Первое слагаемое соответствует случаю, когда первый автомат работает (неважно, что со вторым). Второе слагаемое соответствует случаю, когда первый неисправен, зато работает второй. Убедитесь, что расчет по этой формуле даст тот же самый ре- зультат.
Д1.15. Павел Иванович совершает прогулку из точки A по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Решения задач диагностической работы 1
Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадет в точку G.
Решение. Схема дорожек представляет собой граф 1. А именно — дерево 2. Обычно деревья рисуют корнем вверх, но это неважно. Здесь ребра (ветви) дерева соответству- ют дорожкам. Около каждого ребра напишем вероятность того, что Павел Иванович пройдет по соответствующей дорожке. Выбор пути на каждой развилке происходит наудачу, поэтому вероятность поровну делится между всеми возможностями. Пред- положим, что Павел Иванович пришел в вершину C. Из нее выходит три ребра CH,
3 Таким образом можно расставить все вероятности.
Каждый маршрут из начальной точки A в любую из конечных точек является элементарным событием в этом эксперименте. События здесь не равновозможные. Вероятность каждого элементарного события можно найти по правилу умножения. Нам нужно найти вероятность элементарного события G = {Павел Иванович пришел в точку G }.
1 Графом в математике называется множество точек, некоторые из которых (или все) соединены ли- ниями — дугами, ребрами. Часто точки обозначают состояния какой-либо системы, а ребра — возможные переходы между состояниями. Как это делается, показывают задачи, которые мы предлагаем решить. Це- почки ребер образуют пути в графе. 2 Дерево — частный случай графа. Дерево — такой граф, в котором нет замкнутых путей (циклов). На- звание «дерево» подчеркивает, что получается ветвящаяся конструкция. Решения задач диагностической работы 1 Это событие состоит в том, что Павел Иванович прошел маршрутом ABG. Вероятность находится умножением вероятностей вдоль ребер AB и BG:
2 4 8
Примечание. Для решения задачи мы использовали только маршрут ABG, так как иначе нельзя попасть из A в G. Остальные маршруты нас не интересовали. Поэтому можно их подробно не рисовать. Д1.16. Павел Иванович совершает прогулку из точки A по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку S, другие — в поле F или в болото M. Найдите вероятность того, что Павел Иванович забредет в болото.
Решение. В болото ведут три маршрута. Обозначим вершины на этих маршрутах и напишем на ребрах вдоль этих маршрутов соответствующие вероятности. Осталь- ные маршруты не будем рассматривать. Решения задач диагностической работы 1 Вероятность события «Павел Иванович попадет в болото», равна
2 4 2 4 2 3 12 Вспомогательная задача. В некотором эксперименте вероятность события A рав- на 0, 3. Если событие A наступает, то вероятность события C равна 0, 2, а в противопо- ложном случае вероятность события C равна 0, 4. Найдите вероятность события C.
Описанная схема является общей схемой для многих задач. В таких задачах удобно изобразить эксперимент графически деревом вероятностей. Отличие от предыдущих задач состоит в том, что вероятности на ребрах получаются не из равновозможности, а иначе. Весь эксперимент обозначим буквой Ω (большая омега) и поставим точку около этой буквы — корень дерева, из которого ветви-ребра растут вниз. Из точки Ω прове- дем ребро вниз-влево в точку A. Событие A имеет вероятность 0, 3, поэтому подпишем у этого ребра вероятность 0, 3. Противоположное событие A ¯¯ имеет вероятность 0, 7. Проведем второе ребро в точку A ¯¯. Если осуществилось событие A, то событие C по условию имеет вероятность 0, 2. Поэтому из точки A проведем ребро вниз-влево в точку C и подпишем вероятность. Действуя так же и дальше, достроим все дерево (см. рисунок).
Чтобы найти вероятность события C, нужно выделить только те пути, ко- торые ведут из корневой точки к событию C. На рисунке мы оставили эти пути яркими, а пути, не приводящие к C, изобразили бледно. Выделенные пути Ω A C и Ω A ¯¯ C являются элементарными событиями, благоприятствующими событию C. Теперь нужно вычислить вероятности выделенных путей и сложить их. Поль- зуясь правилами умножения и сложения вероятностей, получаем P(C) = P(Ω AC)+ P(Ω A ¯¯ C) = 0, 3 · 0, 2 + 0, 7 · 0, 4 = 0, 06 + 0, 28 = 0, 34. Применим этот метод к решению заданий диагностической работы. Д1.17. Две фабрики одной фирмы выпускают одинаковые мобильные телефоны. Первая фабрика выпускает 30 % всех телефонов этой марки, а вторая — остальные те- лефоны. Известно, что из всех телефонов, выпускаемых первой фабрикой, 1 % имеют Решения задач диагностической работы 1 скрытые дефекты, а из выпускаемых второй фабрикой — 1, 5 %. Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект. Решение. Введем обозначения для событий: A 1 = {телефон выпущен на первой фабрике} A 2 = {телефон выпущен на второй фабрике}, D = {телефон имеет скрытый дефект}.
По условию задачи легко составить дерево и найти необходимые вероятности. P(D) = 0, 3 · 0, 01 + 0, 7 · 0, 015 = 0, 003 + 0, 0105 = 0, 0135. Д1.18. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40 % яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20 % яиц высшей категории. Всего высшую категорию получает 35 % яиц из этих двух хозяйств. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из пер- вого хозяйства.
Решение. Эта задача обратна предыдущей. Событие «яйцо имеет высшую катего- рию» назовем H. События «яйцо поступило из первого хозяйства» и «яйцо поступило из второго хозяйства» назовем A 1 и A 2 соответственно. Обозначим через p искомую вероятность события A 1 и составим дерево.
Получаем
P(H) = p · 0, 4 + (1 − p)· 0, 2. Решения задач диагностической работы 1 По условию эта величина равна 0, 35. Тогда 0, 4 p + 0, 2(1 − p) = 0, 35, откуда 0, 2 p = 0, 15 и, значит, p = 0, 75. Ответ: 0, 75.
Ответы:
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 782; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.41.187 (0.027 с.) |
 Важно! В следующих задачах для решения удобно использовать дерево вероятно- стей. В части задач дерево построено прямо в условии. В других задачах это дере- во следует построить. Попробуйте решить с помощью дерева вероятностей также некоторые из предыдущих задач, например Д1.13 и Д1.14.
Важно! В следующих задачах для решения удобно использовать дерево вероятно- стей. В части задач дерево построено прямо в условии. В других задачах это дере- во следует построить. Попробуйте решить с помощью дерева вероятностей также некоторые из предыдущих задач, например Д1.13 и Д1.14.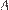

 CK и CL. Поэтому вероятность того, что Павел Иванович выберет ребро CH, равна 1.
CK и CL. Поэтому вероятность того, что Павел Иванович выберет ребро CH, равна 1.


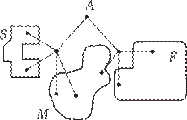
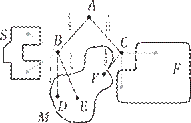
 P(M) = P(ABD)+ P(ABE)+ P(ACF) = 1 · 1 + 1 · 1 + 1 · 1 = 5.
P(M) = P(ABD)+ P(ABE)+ P(ACF) = 1 · 1 + 1 · 1 + 1 · 1 = 5.



 Т1.1
Т1.1 Т1.3
Т1.3 Т1.7
Т1.7


