
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Блок 1. Опыты с равновозможными элементарными исходами
Д1.1. Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя. Решение. Случайный эксперимент — бросание жребия. Элементарное событие в этом эксперименте — участник, который выиграл жребий. Перечислим их:
(Вася), (Петя), (Коля) и (Лёша).
Общее число элементарных событий N равно 4. Жребий подразумевает, что эле- ментарные события равновозможны. Событию A = {жребий выиграл Петя} благоприятствует только одно элементарное событие (Петя). Поэтому N (A)= 1.
N 4 Ответ: 0, 25. Д1.2. Игральный кубик (кость) бросили один раз. Какова вероятность того, что выпало число очков, большее чем 4? Решение. Здесь случайный эксперимент — бросание кубика. Элементарное собы- тие — число на выпавшей грани. Граней всего шесть. Перечислим все элементарные Решения задач диагностической работы 1 события: Значит, N = 6. 1, 2, 3, 4, 5 и 6. Событию A = {выпало больше чем 4} благоприятствуют два элементарных собы- тия: 5 и 6. Поэтому N (A)= 2. Элементарные события равновозможны, поскольку подразумевается, что кубик честный. Поэтому
N 6 3
3 Д1.3. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решение. Орла обозначим буквой О. Решку — буквой Р. В описанном эксперимен- те могут быть следующие элементарные исходы:
Значит, N = 4. ОО, ОР, РО и РР. Событию A = {выпал ровно один орел} благоприятствуют элементарные события ОР и РО. Поэтому N (A)= 2.
N 4 Ответ: 0, 5. Д1.4. В случайном эксперименте бросают два игральных кубика. Найдите вероят- ность того, что в сумме выпадет 8 очков. Решение. Элементарный исход в этом опыте — упорядоченная пара чисел. Первое число выпадает на первом кубике, а второе — на втором. Множество элементарных исходов удобно представить таблицей. Строки соответствуют результату первого брос- ка, столбцы — результату второго броска. Всего элементарных событий N = 36. 1 2 3 4 5 6
2 3 4 5 6 Решения задач диагностической работы 1 Напишем в каждой клетке таблицы сумму выпавших очков и закрасим клетки, где сумма равна 8 (см. рисунок). Таких клеток пять. Значит, событию A = {сумма равна 8} благоприятствуют пять элементарных исходов. Следовательно, N (A) = 5. Поэтому
N 36
36 Д1.5. В случайном эксперименте монету бросили три раза. Какова вероятность того, что орел выпал ровно два раза?
Всего исходов получилось 8. Значит, N = 8. Событию A = {орел выпал ровно два раза} благоприятствуют элементарные собы- тия ООР, ОРО и РОО (они выделены в таблице). Поэтому N (A)= 3.
N 8 Ответ: 0, 375.
Д1.6. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в ко- тором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции. Решение. Элементарный исход — спортсмен, который выступает последним. По- следним может оказаться любой. Всего спортсменов N = 4 + 7 + 9 + 5 = 25. Решения задач диагностической работы 1 Событию A = {последний из Швеции} благоприятствуют только девять исходов (столько, сколько участвует шведских спортсменов). Поэтому N (A)= 9.
= 0, 36. N 25 Ответ: 0, 36. Д1.7. В среднем из 1000 аккумуляторов, поступивших в продажу, 6 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным. Решение. Элементарный исход — случайно выбранный аккумулятор. Поэтому
N = 1000. Событию A = {аккумулятор исправен} благоприятствуют 1000 − 6 = 994 исхода. Поэтому N (A)= 994.
N Ответ: 0, 994. 1000 Примечание. Эту задачу можно решить с помощью формулы вероятности про- N (¯ A ¯)
Значит, P(A)= 1 − P(A ¯¯) = 1 − 0, 006 = 0, 994. N = 0, 006. Д1.8. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. Решение. Элементарное событие — спортсменка, выступающая первой. Поэтому N = 20. Чтобы найти число элементарных событий, благоприятствующих событию A = {первой выступает спортсменка из Китая}, нужно подсчитать число спорсменок из Китая: N (A)= 20 − (8 + 7)= 5. Все элементар- ные события равновозможны по условию задачи, поэтому
= 0, 25.
Ответ: 0, 25. N 20 Примечание. Задачу можно решить с помощью формулы сложения вероятностей несовместных событий. Возьмем события R = {первая из России}, A = {первая из США} и C = {первая из Китая}. Эти события несовместны, их объединение — достоверное событие. Поэтому
20 20 = 0, 25. Д1.9. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно раз- делить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат Решения задач диагностической работы 1 карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе? Решение. Элементарный исход — карточка, выбранная капитаном российской ко- манды; N = 16. Событию A = {команда России во второй группе} благоприятствуют четыре карточки с номером «2», то есть N (A)= 4.
= 0, 25. N 16 Ответ: 0, 25. Примечание. Задачу можно решить короче, если иначе определить элементарные события. Пусть элементарным событием будет не карточка, а номер на карточке. Элементарные события равновозможны, поскольку карточек с разными номерами по- ровну. Тогда N = 4, а N (A)= 1. Здесь важно, что в новом эксперименте элементарные события остались равно- возможными. Нужно быть осторожным при переходе к более простому эксперименту. Например, если при двукратном бросании монеты в качестве элементарного исхода взять число выпавших орлов, то такие события 0, 1 или 2 не будут равновозможными!
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 1186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.61.119 (0.023 с.) |
 Важно! В пяти первых задачах для удобства можно выписать все элементарные события эксперимента.
Важно! В пяти первых задачах для удобства можно выписать все элементарные события эксперимента.
 Тогда P(A)= N (A) = 1 = 0, 25.
Тогда P(A)= N (A) = 1 = 0, 25. P(A)= N (A) = 5.
P(A)= N (A) = 5.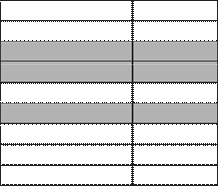 Решение. Орла обозначим буквой О. Решку — буквой Р. В описанном экспери- менте элементарные исходы — тройки, составленные из букв О и Р. Выпишем их все в таблицу:
Решение. Орла обозначим буквой О. Решку — буквой Р. В описанном экспери- менте элементарные исходы — тройки, составленные из букв О и Р. Выпишем их все в таблицу: Важно! В следующих четырех задачах нет нужды выписывать все элементарные исходы. Достаточно подсчитать их количество.
Важно! В следующих четырех задачах нет нужды выписывать все элементарные исходы. Достаточно подсчитать их количество. Тогда P(A)= N (A) = 994 = 0, 994.
Тогда P(A)= N (A) = 994 = 0, 994.


