
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектр собственных значений разностного оператора второй производной.Содержание книги
Поиск на нашем сайте
Известно, что дифференциальная задача на собственные значения Рассмотрим разностный аналог данной задачи на равномерной сетке.
Система разностных уравнений (2) представляет собой систему ЛАУ
Матрица
Разностное уравнение (2) можно представить в эквивалентном виде
Это разностное однородное уравнение второго порядка, общее решение которого может быть выражено в виде комбинации линейно независимых частных решений.
Решение (4) удовлетворяет нулевым краевым условиям при выполнении равенств
Однородная система (6) имеет нетривиальное решение при условии Следовательно, собственные функции, которые для однородного уравнения определяются с точностью до постоянного множителя
Полагая
Заметим, что характер-е уравнение имеет пару комплексно сопряженных решений (5), причем относительно действительной части этих корней имеем Отсюда находим собственные значения, соответствующие полученным собственным функциям: Окончательно приходим к следующему набору собственных функций и собственных значений дискретной задачи:
Заметим примечательный факт, что набор собственных функций дискретной задачи совпадает в узлах сетки с соответствующими собственными функциями дифференциальной задачи при
Отметим основные отличия собственных значений дискретной задачи от собственных значений дифференциальной задачи. 1. Спектр собственных значений дискретной задачи при любом конечном числе узлов сетки ограничен, и максимальное собственное значение зависит от шага сетки
Для сравнения, спектр дифференциальной задачи неограничен: 2. Для любого фиксированного Несложно заметить также, что собственные значения дискретной задачи при любом конечном значении шага сетки меньше соответствующих собственных значений дифференциальной задачи. Это непосредственно следует из неравенства
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.85.245 (0.007 с.) |

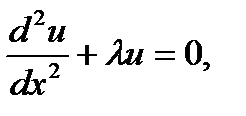
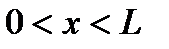
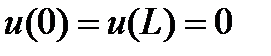 (1) имеет бесконечный спектр собственных значений и соответствующих им собственных функций
(1) имеет бесконечный спектр собственных значений и соответствующих им собственных функций 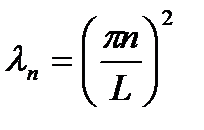 ,
, 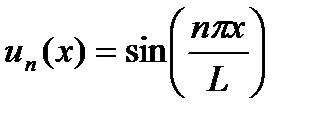 ,
, 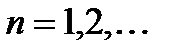 .
.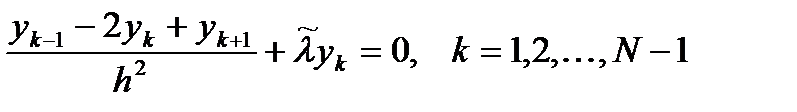 , (2)
, (2)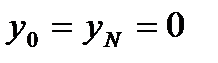 ,
, 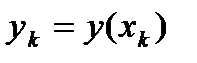 ,
, 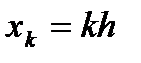 ,
, 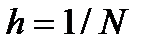 .
.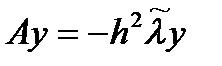 с трехдиагональной симметричной квадратной матрицей
с трехдиагональной симметричной квадратной матрицей 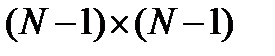
 .
.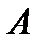 имеет диагональное преобладание и у нее имеется
имеет диагональное преобладание и у нее имеется 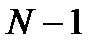 собственных значений. Данная матрица может рассматриваться как разностный аналог дифференциального оператора второй производной.
собственных значений. Данная матрица может рассматриваться как разностный аналог дифференциального оператора второй производной.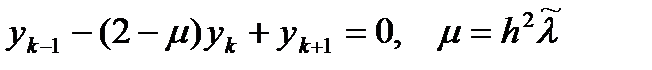 . (3)
. (3) (4), где
(4), где 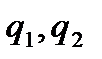 - корни характеристического многочлена
- корни характеристического многочлена
 . (5)
. (5)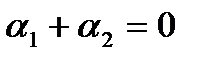 ,
, 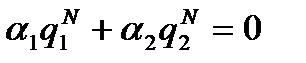 . (6)
. (6)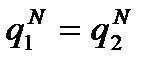 . Учитывая, что для корней характеристического уравнения (5) (это доказывается прямыми вычислениями)
. Учитывая, что для корней характеристического уравнения (5) (это доказывается прямыми вычислениями) 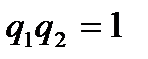 , имеем
, имеем 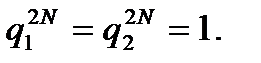
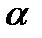 , имеют вид
, имеют вид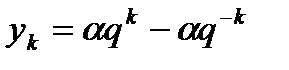 , где
, где 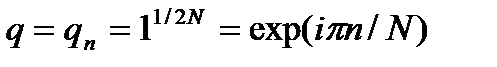 ,
, 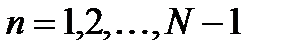 .
.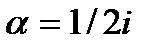 и используя формулу Эйлера, окончательно получаем вид собственных функций разностной задачи
и используя формулу Эйлера, окончательно получаем вид собственных функций разностной задачи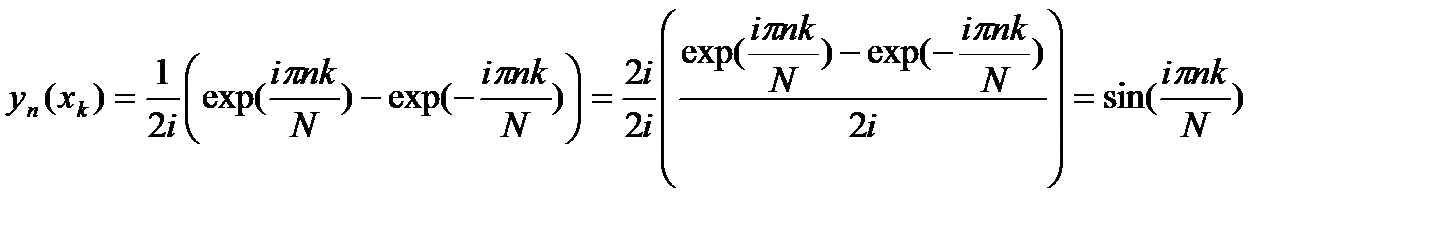 .
.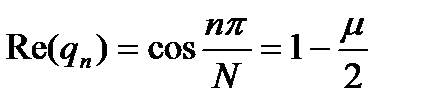 .
.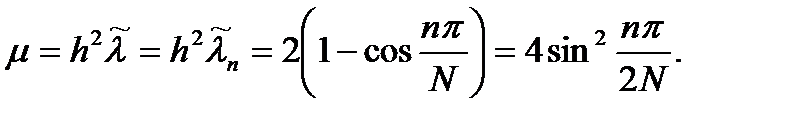
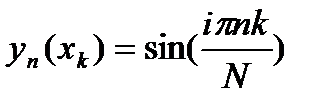 ,
, 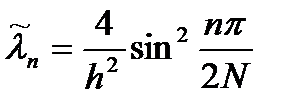 ,
, 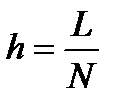 :
: 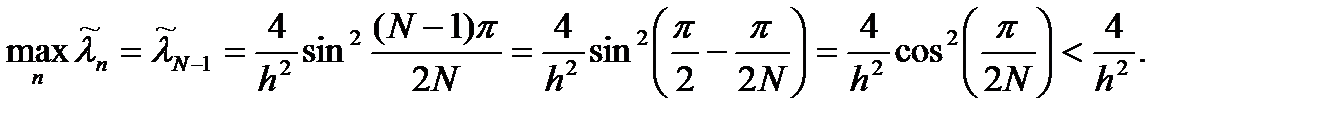
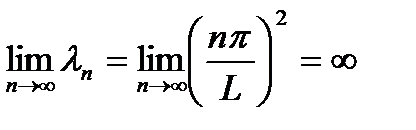 .
.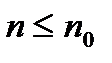 собственные значения дискретной задачи сходятся к соответствующим собственным значениям дифференциальной задачи при
собственные значения дискретной задачи сходятся к соответствующим собственным значениям дифференциальной задачи при 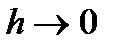 :
:  .
.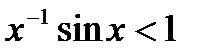 при любом
при любом 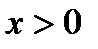 . Структура собственных значений дискретной задачи позволяет заметить также, что все собственные значения, как и в случае дифференциальной задачи, положительны, различны и возрастают с ростом
. Структура собственных значений дискретной задачи позволяет заметить также, что все собственные значения, как и в случае дифференциальной задачи, положительны, различны и возрастают с ростом 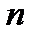 (последнее следует из свойства монотонного возрастания функции
(последнее следует из свойства монотонного возрастания функции 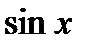 на интервале
на интервале 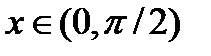 ).
).


