
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Итерационные методы решения проблемы собственных значений. Степенной метод.Содержание книги
Поиск на нашем сайте
Число Вектор Уравнение (1) имеет нетривиальные решения ó Функция Степенной метод: Пусть нужно найти макс. по модулю собственное значение Заметим, что при умножении матрицы на ее собственный вектор последний преобразуется в коллинеарный вектор Т.к. Заметим, что асимптотика Использование итерационной процедуры (4) позволяет определить как собственный вектор, соответств-й макс собств. значению, так и величину собств. значения
После того как наибольшее собственное значение определено, данный подход может быть использован для вычисление других собственных значений и собственных векторов. Недостаток степенного метода: не может быть использован в случае, когда матрица имеет равные по модулю собственные значения. Итерационный процесс (4) в этом случае не сходится. Есть возможность находить степенным методом комплексные характеристические числа и соответствующие инвариантные подпространства для вещественных матриц.
|
||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 185; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.208.236 (0.008 с.) |

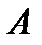 порядка - квадратная невырожденная матрица
порядка - квадратная невырожденная матрица 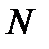 .
.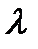 называется собственным значением матрицы
называется собственным значением матрицы 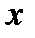 , удовлетворяющий равенству
, удовлетворяющий равенству 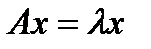 (1)
(1)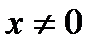 , удовлетворяющий равенству (1), называется собственным вектором матрицы
, удовлетворяющий равенству (1), называется собственным вектором матрицы  (2)
(2)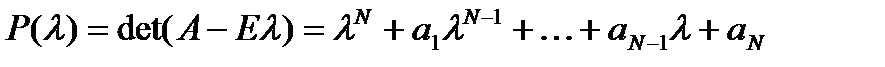 - характеристический многочлен матрицы. Множество его корней совпадает со спектром.
- характеристический многочлен матрицы. Множество его корней совпадает со спектром.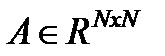 , причем, искомое собственное значение простое. Пусть
, причем, искомое собственное значение простое. Пусть  .
.  , причем длина полученного при этом вектора изменяется пропорционально соответствующему собственному значению
, причем длина полученного при этом вектора изменяется пропорционально соответствующему собственному значению 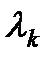 . Данное свойство собственных векторов лежит в основе степенного метода. У матриц простой структуры система собственных векторов образует базис в
. Данное свойство собственных векторов лежит в основе степенного метода. У матриц простой структуры система собственных векторов образует базис в 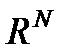 , любой вектор может быть представлен:
, любой вектор может быть представлен: 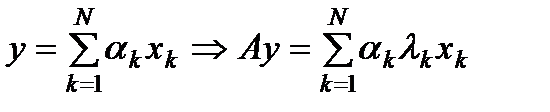 => в разложении по собственным векторам при умножении матрицы на вектор наибольший рост (наименьшее убывание) испытывает составляющая, соответствующая максимальному собственному значению. Рассмотрим последовательность
=> в разложении по собственным векторам при умножении матрицы на вектор наибольший рост (наименьшее убывание) испытывает составляющая, соответствующая максимальному собственному значению. Рассмотрим последовательность 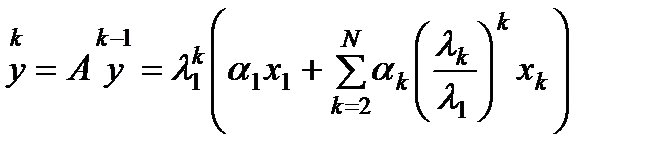 (3)
(3) , то при
, то при 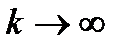
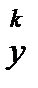 сходится к собственному вектору
сходится к собственному вектору 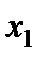 . Компоненты вектора
. Компоненты вектора 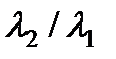 – знаменателем геометрической прогрессии самой медленной из компонент
– знаменателем геометрической прогрессии самой медленной из компонент 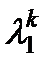 , которое в пределе
, которое в пределе 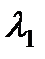 => нужна нормировка промежуточных результатов. В качестве нормировочного коэффициента наиболее подходящий выбор –
=> нужна нормировка промежуточных результатов. В качестве нормировочного коэффициента наиболее подходящий выбор – 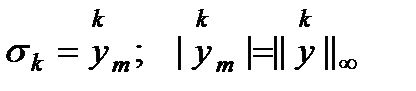 (
(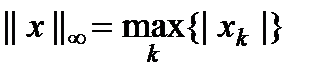 ) =>
) => 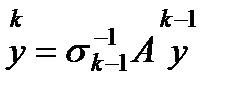 (4)
(4)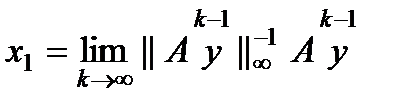 , (5)
, (5) 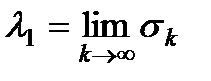 . (6)
. (6)


