
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Гаусса с выбором ведущего элементаСодержание книги
Поиск на нашем сайте
Метод Гаусса Большинство прямых методов решения СЛАУ в той или иной мере наследуют идею алгоритма последовательного исключения неизвестных – метода Гаусса. Если матрица задачи, например, является верхней треугольной, то произвольное k-ое уравнение системы имеет вид Последнее уравнение системы содержит всего лишь одно неизвестное Остальные неизвестные вычисляются последовательно по явным формулам
Аналогичный алгоритм м.б. построен для задачи с нижней треугольной матрицей. Суть метода Гаусса состоит в приведении матрицы задачи к верхнему (нижнему) треугольному виду. Для этих целей используются тождественные преобразования системы. В частности, решение задачи не меняется при замене произвольной строки системы на линейную комбинацию данной строки и произвольного числа других строк системы. Используя такого рода преобразования, можно последовательно, столбец за столбцом, исключить переменные, находящиеся ниже главной диагонали системы ЛАУ. Элементарный шаг такого преобразования можно выразить с помощью операции умножения л. и пр. части системы на элементарную нижнюю треугольную матрицу вида:
Матрицы Нетрудно убедиться, что после выполнения описанных действий матрица Таким образом, метод последовательного исключения Гаусса состоит в преобразовании исходной системы уравнений путем умножения ее на элементарные треугольные матрицы, в результате чего исходная система преобразуется в эквивалентную систему с верхней треугольной матрицей Решение полученной системы уравнений находится с помощью алгоритма (4), (5). Процедуру (7) – (9) принято называть прямым ходом метода Гаусса, а (4), (5) – соответственно обратный ход.
Оценим вычислительные затраты прямого и обратного хода метода Гаусса. Одна операция умножения В самом деле, каждый элемент матричного произведения находится как скалярное произведение двух векторов, причем вектор первого из сомножителей имеет не более двух ненулевых элементов (строка). В результате каждый из Для обратного хода метода Гаусса из выражения (5) легко подсчитать, что для вычисления Метод Гаусса является самым универсальным в своем классе и может быть использован для решения произвольных СЛАУ с невырожденной матрицей. Тем не менее, источником проблем являются нулевые (близкие к нулю) значения диагональных элементов, присутствующие в матрице изначально, либо появляющиеся в процессе исключения неизвестных. Как видно из выражения (6), при формировании матриц Основные понятия теории разностных схем. Пространство сеточных функций и сеточные нормы.
Для численного решения задач по дифференциальным уравнениям методом сеток (конечных разностей) необходимо проделать следующее. Область непрерывного изменения аргумента (аргументов) искомой функции заменяется конечным дискретным множеством точек, называемых узлами сетки. Все производные, входящие в дифференциальную задачу, заменяются разностными производными. Это осуществляется тем или иным методом конструирования разностных схем. В конечном итоге получаем систему алгебраических уравнений. Таким образом, сущность метода сеток состоит в замене исходных дифференциальных задач системами алгебраических уравнений, их приближенно заменяющими. Если при измельчении шагов сетки решение разностной схемы сходится к решению исходной дифференциальной задачи, то за решение исходной задачи принимается решение разностной схемы. После конструирования разностной схемы необходимо провести теоретические исследования разрешимости задач. Внутренними свойствами разностной схемы являются аппроксимация и устойчивость. Эти свойства разностной схемы должны исследоваться для каждой схемы. Получающиеся разностные схемы решаются теми или иными методами решения систем алгебраических уравнений. Разрешающий алгоритм должен быть экономичным и этим же требованиям должна обладать и разностная схема.
Сеточная область Для построения разностной схемы необходимо построить сетку Gh - конечное множество точек, принадлежащих G, плотность распределения которых характеризуется параметрами h-шагом сетки. Пусть область изменения аргумента x есть отрезок G={0≤x≤1}. Разобьем этот отрезок точками xi=i∙h, i=0,n на n равных частей длины h=1/n каждая. Множество точек xi=i∙h, называется равномерной сеткой на отрезке 0≤x≤1 и обозначим Разбиение отрезка 0≤x≤1 точками xi, i=0,n можно производить произвольным образом: 0<x1<…<xn-1<1. Тогда получаем сетку Метод Ньютона Основная идея метода Ньютона состоит в выделении из уравнений линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности линейных систем. Рассмотрим систему уравнений: в предположении, что Полагая Опишем общий шаг метода. Пусть уже получено приближение Очередное приближение Если матрица Якоби Таким образом, в основе метода Ньютона лежит идея линеаризации вектор-функции Через уже известное приближение
Точное условие сходимости метода Ньютона имеет достаточно сложный вид. Но очевидный результат: в достаточно малой окрестности корня итерации сходятся, если матрица Якоби невырожденная, причём сходимость квадратичная. Пусть в
Теорема (о сходимости). Пусть 1) вектор-функция 2) для всех 3) для всех 4) Тогда метод Ньютона (3) 1) 2) 3) Замечание. Оценка погрешности метода Ньютона: Метод Гаусса Большинство прямых методов решения СЛАУ в той или иной мере наследуют идею алгоритма последовательного исключения неизвестных – метода Гаусса. Если матрица задачи, например, является верхней треугольной, то произвольное k-ое уравнение системы имеет вид Последнее уравнение системы содержит всего лишь одно неизвестное Остальные неизвестные вычисляются последовательно по явным формулам
Аналогичный алгоритм м.б. построен для задачи с нижней треугольной матрицей. Суть метода Гаусса состоит в приведении матрицы задачи к верхнему (нижнему) треугольному виду. Для этих целей используются тождественные преобразования системы. В частности, решение задачи не меняется при замене произвольной строки системы на линейную комбинацию данной строки и произвольного числа других строк системы. Используя такого рода преобразования, можно последовательно, столбец за столбцом, исключить переменные, находящиеся ниже главной диагонали системы ЛАУ. Элементарный шаг такого преобразования можно выразить с помощью операции умножения л. и пр. части системы на элементарную нижнюю треугольную матрицу вида:
Матрицы Нетрудно убедиться, что после выполнения описанных действий матрица Таким образом, метод последовательного исключения Гаусса состоит в преобразовании исходной системы уравнений путем умножения ее на элементарные треугольные матрицы, в результате чего исходная система преобразуется в эквивалентную систему с верхней треугольной матрицей Решение полученной системы уравнений находится с помощью алгоритма (4), (5). Процедуру (7) – (9) принято называть прямым ходом метода Гаусса, а (4), (5) – соответственно обратный ход.
Оценим вычислительные затраты прямого и обратного хода метода Гаусса. Одна операция умножения В самом деле, каждый элемент матричного произведения находится как скалярное произведение двух векторов, причем вектор первого из сомножителей имеет не более двух ненулевых элементов (строка). В результате каждый из Для обратного хода метода Гаусса из выражения (5) легко подсчитать, что для вычисления Метод Гаусса является самым универсальным в своем классе и может быть использован для решения произвольных СЛАУ с невырожденной матрицей. Тем не менее, источником проблем являются нулевые (близкие к нулю) значения диагональных элементов, присутствующие в матрице изначально, либо появляющиеся в процессе исключения неизвестных. Как видно из выражения (6), при формировании матриц Метод Гаусса с выбором ведущего элемента При перестановке строк СЛАУ решение задачи не изменяться. Данное свойство лежит в основе алгоритмов упорядочения строк матрицы. Стратегия частичного упорядочения состоит в следующем. Прежде чем приступить к формированию матрицы Алгоритмически перестановку строк матрицы можно реализовать путем умножения матрицы перестановок на преобразуемую матрицу. Матрицей перестановок называется матрица, в каждой строке и каждом столбце которой содержится только один ненулевой элемент, равный единице, а остальные элементы равны нулю. Частным случает матрицы перестановок является единичная матрица. Элементарной матрицей перестановки называется матрица Матрицы перестановок обладают рядом замечательных свойств. - Матрица перестановок является унитарной матрицей: - Произведение любого числа матриц перестановок является матрицей перестановок. - Произвольную перестановку строк матрицы можно осуществить с помощью матрицы перестановок, полученной из произведения элементарных матриц перестановок. Алгоритм частичного упорядочения с выбором главного элемента по столбцам фактически состоит в определении позиции главного элемента и построении элементарной матрицы перестановок. Пусть, например, при исключении неизвестных в СЛАУ с матрицей 5 x5 после двух шагов исключения неизвестных имеем, что ведущий элемент
Использование Замечание 1. Кроме рассмотренного алгоритма частичного упорядочения с выбором главного элемента по столбцам существуют аналогичные варианты упорядочения по строкам, а также по строкам и столбцам одновременно. Замечание 2. Надежность алгоритма частичного упорядочения существенно повышается, если матрица системы ЛАУ масштабирована таким образом, что максимальные значения модулей элементов в каждой строке и каждом столбце имеют одинаковый порядок. Если матрица не отвечает требованиям масштабирования полезно, по крайней мере, предварительно выполнить нормировку строк, нарушающих баланс матрицы. Замечание 3. Среди немногочисленных случаев, когда частичное упорядочение оказывается излишним, можно отметить диагонально-доминирующие и симметричные положительно-определенные матрицы.
|
||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

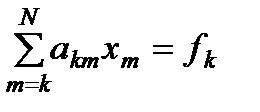 ,
, 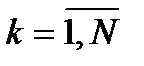 ,
, 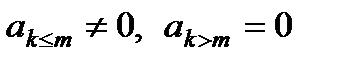 (3)
(3)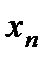 , и его значение вычисляется первым:
, и его значение вычисляется первым: 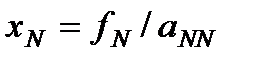 (4)
(4)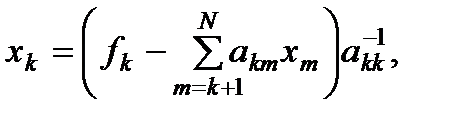
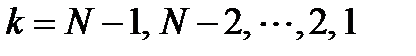 (5)
(5) 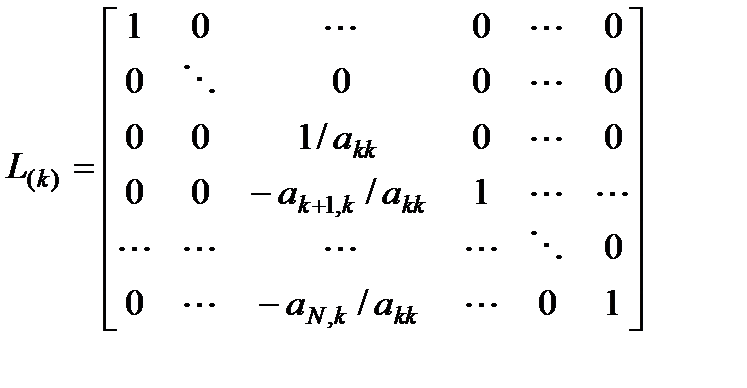 (6)
(6)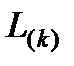 отличаются от единичной тем, что
отличаются от единичной тем, что 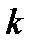 -ый столбец данной матрицы, начиная с элемента
-ый столбец данной матрицы, начиная с элемента 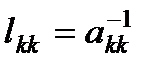 , и ниже
, и ниже 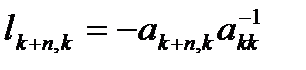 ,
, 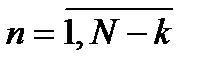 , формируется специальным образом (6) из соответствующих значений элементов преобразуемой матрицы. В результате умножения
, формируется специальным образом (6) из соответствующих значений элементов преобразуемой матрицы. В результате умножения 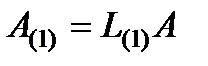 (7) преобразованная матрица
(7) преобразованная матрица 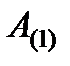 будет иметь нулевые значения элементов первого столбца ниже главной диагонали:
будет иметь нулевые значения элементов первого столбца ниже главной диагонали: 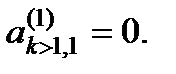 Далее, на основе элементов матриц
Далее, на основе элементов матриц 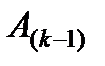 ,
, 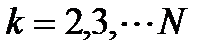 последовательно формируются матрицы
последовательно формируются матрицы 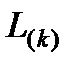 и находятся
и находятся 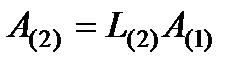 ,
, 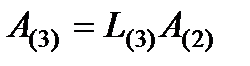 , …
, … 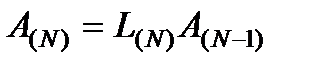 (8)
(8)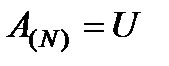 будет верхней треугольной матрицей с единицами на главной диагонали.
будет верхней треугольной матрицей с единицами на главной диагонали.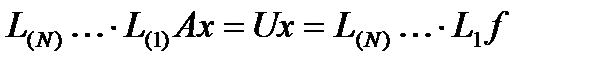 (9)
(9)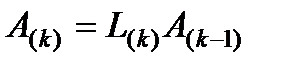 имеет выч-ю сложность порядка
имеет выч-ю сложность порядка 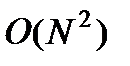 .
.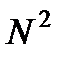 элементов матрицы
элементов матрицы 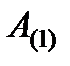 вычисляется не более чем за два умножения и одно сложение. Несложно заметить, что в процессе умножения
вычисляется не более чем за два умножения и одно сложение. Несложно заметить, что в процессе умножения 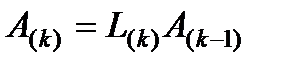 элементы матрицы
элементы матрицы 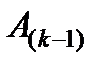 , расположенные выше
, расположенные выше 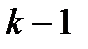 -ой строки и левее
-ой строки и левее 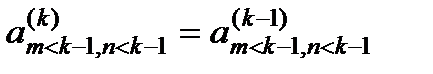 . По этой причине вычислительная сложность умножения матриц
. По этой причине вычислительная сложность умножения матриц 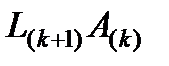 уменьшается с ростом
уменьшается с ростом 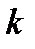 и не превосходит
и не превосходит 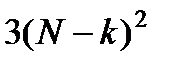 . Таким образом, вычислительные затраты на реализацию прямого хода метода Гаусса составляют
. Таким образом, вычислительные затраты на реализацию прямого хода метода Гаусса составляют 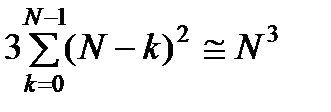 операций умножения и сложения. Формирование матриц
операций умножения и сложения. Формирование матриц 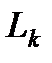 требует приблизительно
требует приблизительно 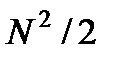 операций. С учетом вышесказанного для матриц достаточно большой размерности
операций. С учетом вышесказанного для матриц достаточно большой размерности 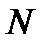 можно оценить выч-ю сложность прямого хода метода Гаусса величиной
можно оценить выч-ю сложность прямого хода метода Гаусса величиной 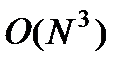 .
.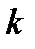 -ой компоненты решения требуется
-ой компоненты решения требуется 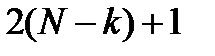 операций. Суммирование вычислительных затрат для определения всех
операций. Суммирование вычислительных затрат для определения всех 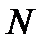 неизвестных дает приблизительно
неизвестных дает приблизительно 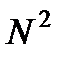 операций, что на порядок меньше вычислительной сложности прямого метода Гаусса.
операций, что на порядок меньше вычислительной сложности прямого метода Гаусса.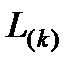 выполняется деление на
выполняется деление на 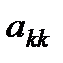 , что в случае
, что в случае 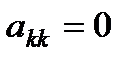 приводит к потере корректности алгоритма. Для устранения этих проблем используется алгоритмы перестановок столбцов (строк) матрицы.
приводит к потере корректности алгоритма. Для устранения этих проблем используется алгоритмы перестановок столбцов (строк) матрицы.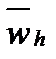 ={xi=i∙h, i=0,n}, а число h - расстояние между точками (узлами) сетки называется шагом сетки.
={xi=i∙h, i=0,n}, а число h - расстояние между точками (узлами) сетки называется шагом сетки.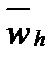 ={xi, i=0,n, x0=0, xn=1} c шагами hi=xi-xi-1, которые зависит от номера узла сетки. Если hi≠hi+1 хотя бы в одной точке, то сетка называется неравномерной и такую сетку обозначают ŵ
={xi, i=0,n, x0=0, xn=1} c шагами hi=xi-xi-1, которые зависит от номера узла сетки. Если hi≠hi+1 хотя бы в одной точке, то сетка называется неравномерной и такую сетку обозначают ŵ  . Точки x0 и xn назовем граничными узлами и обозначим их гh. Остальные узлы назовем внутренними и обозначим их wh. Узлы, соседние с граничащими, назовем приграничными. Тогда имеем
. Точки x0 и xn назовем граничными узлами и обозначим их гh. Остальные узлы назовем внутренними и обозначим их wh. Узлы, соседние с граничащими, назовем приграничными. Тогда имеем 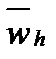 =wh
=wh  гh.
гh.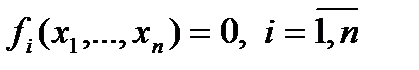
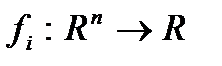 – непрерывно-дифференцируемые функции.
– непрерывно-дифференцируемые функции.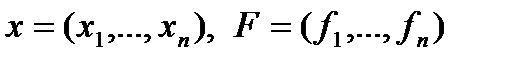 , перейдём к векторной записи
, перейдём к векторной записи 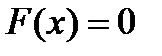 (2)
(2)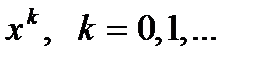 Разложим функцию
Разложим функцию 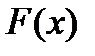 в ряд Тейлора, оставив только два первых члена в силу малости отклонения приближения
в ряд Тейлора, оставив только два первых члена в силу малости отклонения приближения 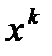 от корня:
от корня: 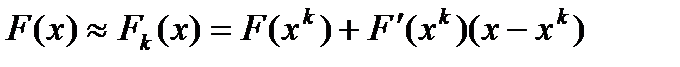 ,
, 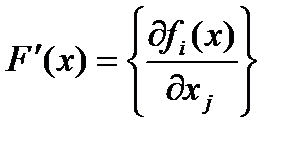 – матрица Якоби для
– матрица Якоби для 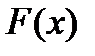 .
.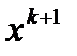 определяется как решение линейной системы
определяется как решение линейной системы 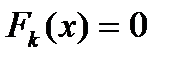 , т.е.
, т.е. 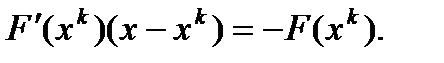
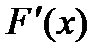 не вырождена, то решение системы линейной системы можно записать в явном виде, что приводит к стандартной формуле метода Ньютона
не вырождена, то решение системы линейной системы можно записать в явном виде, что приводит к стандартной формуле метода Ньютона 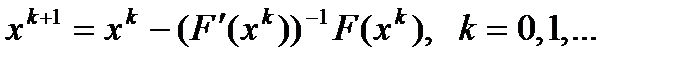 (3)
(3)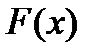 в окрестности каждого приближения (на каждой итерации), что позволяет свести решение системы (2) к последовательному решению линейных систем.
в окрестности каждого приближения (на каждой итерации), что позволяет свести решение системы (2) к последовательному решению линейных систем.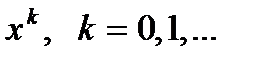 к корню
к корню 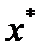 можно записать, что
можно записать, что 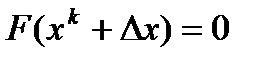 , где
, где 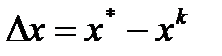 . Тогда после линеаризации получим систему уравнений, линейную относительно
. Тогда после линеаризации получим систему уравнений, линейную относительно 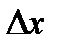 . Таким образом, на каждом шаге мы будем находить приращения
. Таким образом, на каждом шаге мы будем находить приращения 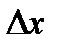 , и новое приближение к решению по формулам:
, и новое приближение к решению по формулам: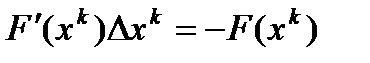 – система линейных уравнений.
– система линейных уравнений.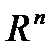 выбрана нек-я векторная
выбрана нек-я векторная 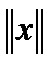 и согласованная с ней матричная
и согласованная с ней матричная 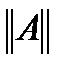 .
.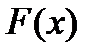 определена и непрерывно-дифференцируема в области
определена и непрерывно-дифференцируема в области 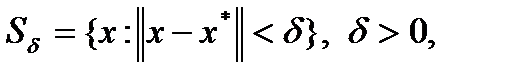 где
где 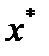 – решение уравнения (2),
– решение уравнения (2),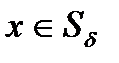 существует обратная матрица
существует обратная матрица 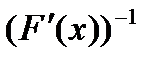 , причём
, причём 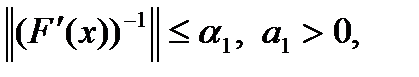
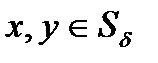
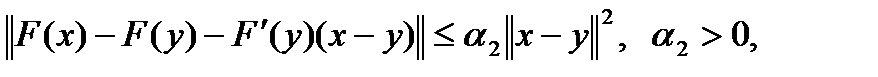
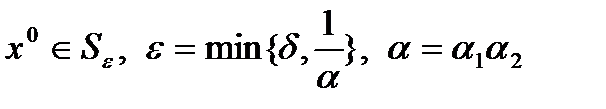
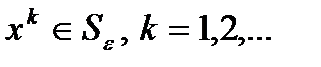
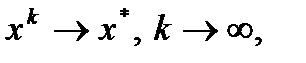
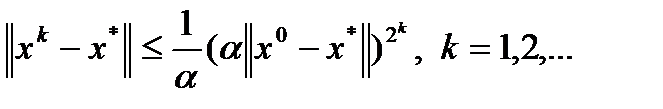
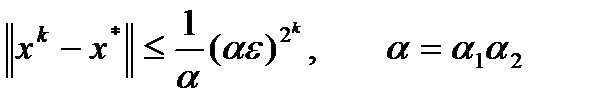
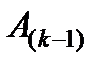 с номерами
с номерами 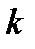 и
и 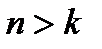 , причем значение
, причем значение 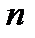 определяется из условия
определяется из условия 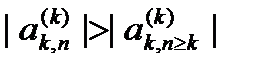 . Таким образом, на позиции ведущего элемента
. Таким образом, на позиции ведущего элемента 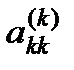 после перестановки строк оказывается максимальный по модулю из элементов
после перестановки строк оказывается максимальный по модулю из элементов 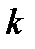 -го столбца, расположенных ниже главной диагонали. Использование данных перестановок позволяет избежать деления на нуль при формировании матриц
-го столбца, расположенных ниже главной диагонали. Использование данных перестановок позволяет избежать деления на нуль при формировании матриц 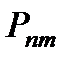 , полученная из единичной матрицы путем перестановки в ней строк с номерами
, полученная из единичной матрицы путем перестановки в ней строк с номерами 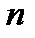 и
и 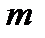 . Умножение матрицы
. Умножение матрицы 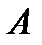 приводит к перестановке в последней
приводит к перестановке в последней 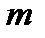 -ой строк.
-ой строк.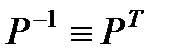 .
.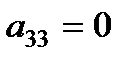 , максимальный элемент третьего столбца находится в четвертой строке:
, максимальный элемент третьего столбца находится в четвертой строке: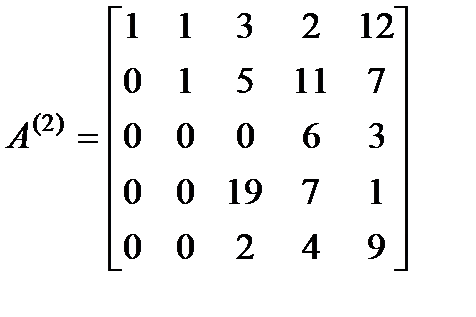 . Тогда
. Тогда 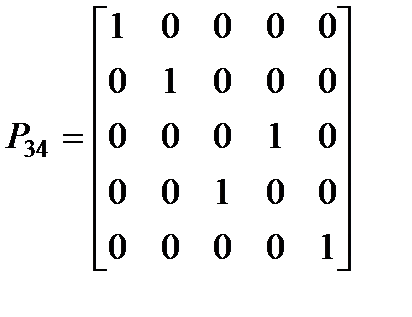 ,
, 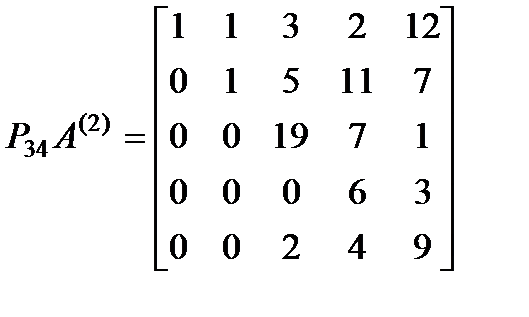
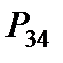 позволяет предотвратить деление на нуль. Далее, формируется матрица
позволяет предотвратить деление на нуль. Далее, формируется матрица 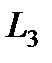 , вычисляется
, вычисляется 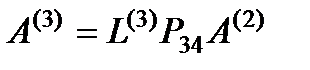 и выполняется следующий шаг исключения.
и выполняется следующий шаг исключения.


