
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычислительная сложность итерационных методов. Число итераций.Содержание книги
Поиск на нашем сайте Точное решение задачи неизвестно=>для оценки погрешности текущего итер. приближения используется невязка приближ. реш-я, связанная с ошибкой соотношением:
При сходимости итер-го процесса норма погрешности убывает пропорционально невязке =>в качестве критерия остановки итераций традиционно используется условие Кол-во итераций для достижения заданной точности можно оценить, зная норму матрицы итерационного процесса. Норма матрицы итерационного процесса Можно также использовать переобусловливатель 6.1. Неявные итерационные методы (Зейделя, Якоби, Последовательной верхней релаксации) - стационарные
Итерационный процесс (2) приводит к решению (1) ó 3. последовательность векторов 4. предел данной последовательности является решением (1). Из 2 => где В случае плохо обусловленных матриц (число обусловленности большое, не стремится к 1) сходимость итерационных методов вида (2), (3) с оператором Неявный итерационный метод вида Основное функциональное назначение матрицы Второе при выборе переобусловливателя: возможности вычисления матрицы Из функционального назначения идеальным переобусловливателем является матрица Метод Якоби. Метод Зейделя (Гаусса-Зейделя). Матрица Метод последовательной верхней релаксации. В некотором роде является обобщением метода Зейделя и метода Якоби. Переобусловливатель строится из верхней треугольной части матрицы ( При Для реализации этих трех методов не нужно знания спектра задачи.
|
||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 668; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

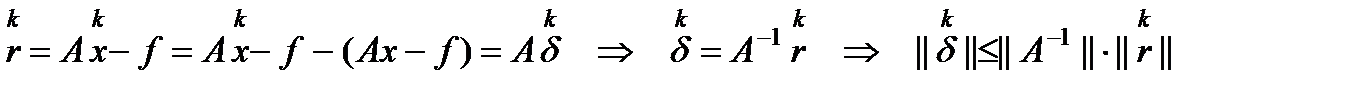 .
. 
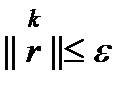 (8)
(8)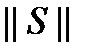 характеризует скорость его сходимости. Максимальная скорость сходимости достигается при минимальном значении
характеризует скорость его сходимости. Максимальная скорость сходимости достигается при минимальном значении 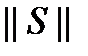 .
. 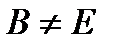 для уменьшения числа итераций для достижения заданной точности решения.
для уменьшения числа итераций для достижения заданной точности решения.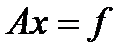 (1) с невырожденной матрицей
(1) с невырожденной матрицей 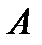
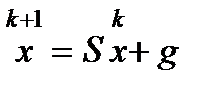 ,
, 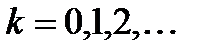 , (2), где
, (2), где 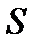 – матрица итерационного метода,
– матрица итерационного метода, 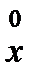 – начальное приближение. Последовательность
– начальное приближение. Последовательность 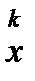 ,
, 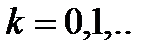 - итерационные приближения решения.
- итерационные приближения решения.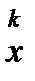 ,
, 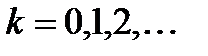 , сходится.
, сходится.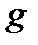 могут быть заданы в виде:
могут быть заданы в виде: 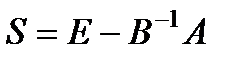 ,
, 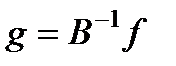 (3)
(3)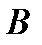 – произвольная невырожденная матрица (для условия 1).
– произвольная невырожденная матрица (для условия 1).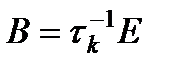 может оказаться очень медленной => использование неявных итерационных методов или итерационных методов с переобусловливателем.
может оказаться очень медленной => использование неявных итерационных методов или итерационных методов с переобусловливателем.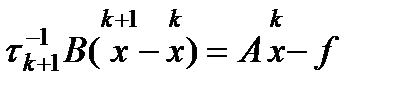 (4) эквивалентен явному итерационному методу
(4) эквивалентен явному итерационному методу 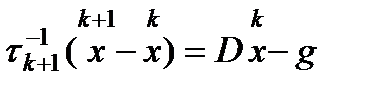 (5), где
(5), где 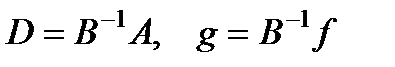 .
.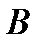 в том, чтобы в итерационных процессах (4) и (5) достичь существенного уменьшения числа обусловленности матрицы
в том, чтобы в итерационных процессах (4) и (5) достичь существенного уменьшения числа обусловленности матрицы 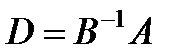 по сравнению с числом обусловленности исходной матрицы
по сравнению с числом обусловленности исходной матрицы 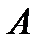 .
.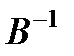 (решения системы
(решения системы 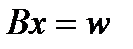 ) намного эффективнее, чем обращение матрицы
) намного эффективнее, чем обращение матрицы 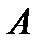 (
(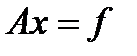 ).
).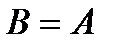 . Но с точки зрения вычислительной эффективности выбор оказывается абсолютно бесполезным, т.к. он возвращает снова к необходимости решения
. Но с точки зрения вычислительной эффективности выбор оказывается абсолютно бесполезным, т.к. он возвращает снова к необходимости решения 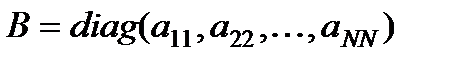 . В качестве переобусловливателя используется диагональная матрица, элементы которой совпадают с диагональными элементами матрицы
. В качестве переобусловливателя используется диагональная матрица, элементы которой совпадают с диагональными элементами матрицы 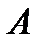 . Выбор диагонального переобусловливателя практически не увеличивает вычислительную сложность отдельной итерации по сравнению с явным методом. Данный метод может оказаться полезным для разреженных матриц с диагональным преобладанием в случае, когда диагональные элементы матрицы
. Выбор диагонального переобусловливателя практически не увеличивает вычислительную сложность отдельной итерации по сравнению с явным методом. Данный метод может оказаться полезным для разреженных матриц с диагональным преобладанием в случае, когда диагональные элементы матрицы 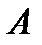 существенно отличаются друг от друга. Такие матрицы возникают, например, при дискретизации многомерных уравнений математической физики с сильно неоднородными коэффициентами. Если диагональные элементы матрицы
существенно отличаются друг от друга. Такие матрицы возникают, например, при дискретизации многомерных уравнений математической физики с сильно неоднородными коэффициентами. Если диагональные элементы матрицы 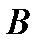 имеет треугольный вид и строится непосредственно из соответствующих элементов матрицы
имеет треугольный вид и строится непосредственно из соответствующих элементов матрицы 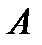 . В силу треугольности матрицы
. В силу треугольности матрицы 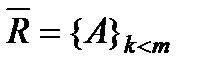 и диагональных элементов матрицы:
и диагональных элементов матрицы: 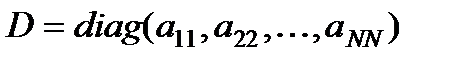 :
: 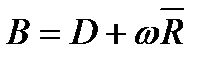 ,
, 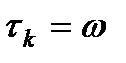 ,
, 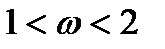
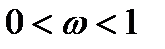 нижняя релаксация, A=A*>0,
нижняя релаксация, A=A*>0, 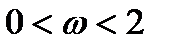 => метод релаксации сходится)
=> метод релаксации сходится)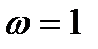 метод последовательной верхней релаксации совпадает с методом Зейделя, при
метод последовательной верхней релаксации совпадает с методом Зейделя, при 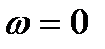 – метод совпадает с методом Якоби. Оптимальное значение параметра
– метод совпадает с методом Якоби. Оптимальное значение параметра 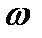 обычно лежит в интервале
обычно лежит в интервале 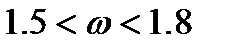 . В большинстве случаев метод последовательной верхней релаксации превосходит по эффективности методы Якоби и Зейделя. Метод популярен для многомерных задач математической физики.
. В большинстве случаев метод последовательной верхней релаксации превосходит по эффективности методы Якоби и Зейделя. Метод популярен для многомерных задач математической физики. 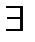 -т модификации данного метода, основанные на чередовании верхней и нижней треугольных матриц в
-т модификации данного метода, основанные на чередовании верхней и нижней треугольных матриц в 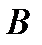 .
.


