Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие устойчивости численных методов для жестких систем. Метод Гира.Содержание книги
Поиск на нашем сайте
Рассмотрим модельную задачу для системы уравнений
Система ДУ В случае, когда система ДУ имеет стандартный вид
Т.к. матрица A, вообще говоря, зависит от решения задачи, то система уравнений может оказаться жесткой на интервале (ах), где собственные значения A обладают свойством (3). Для модельной задачи (1) собственные числа совпадают с коэффициентами Разностное уравнение (5) является однородным и характеристические корни данного уравнения, вообще говоря, отличны от корней характеристического уравнения Таким образом, модельная задача позволяет заметить, что пр. ч. системы уравнений при грубых шагах сетки может оказать влияние на устойчивость разностной задачи => для жестких систем следует использовать такие численные схемы, для кот-х устойчивость разностной задачи не зависит от величины
Компоненты, соответствующие большим отрицательным Опр-е. Разностный метод называется А-устойчивым, если область его устойчивости сод-т левую полуплоскость комплексной плоскости, т.е. если он устойчив при Понятие А -устойчивости означает абсолютную устойчивость метода для дифференциальных задач, асимптотически устойчивых по Ляпунову. Утверждение 1. Среди неявных линейных многошаговых методов отсутствуют А-устойчивые методы. имеющие порядок точности выше второго. Утверждение 2. Не существует явных А-устойчивых численных методов. Для численного решения жестких систем рекомендуется использовать метод Гира. Эти методы можно охарактеризовать как класс чисто неявных многошаговых методов (пр. часть системы учитывается в разностном ур-ии только в одном узле, текущем, в кот-м вычисл-ся зн-е неизвестного решения) вида (4), у которых Порядок локальной точности метода Гира совпадает с порядком разностного уравнения. Коэффициенты метода Гира находятся однозначно из системы уравнений
а коэффициент Эта система пол-ся при рассмотрении невязки разностного метода путем приравнивания к нулю членов одинакового порядка малости от нулевого до
|
||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.110.182 (0.007 с.) |

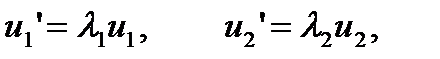 (1), где
(1), где 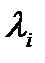 - произвольные комплексные числа.
- произвольные комплексные числа.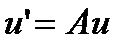 (2) с матрицей
(2) с матрицей 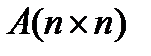 - жесткая, если собственные числа матрицы A:
- жесткая, если собственные числа матрицы A: 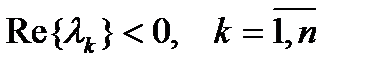 , т.е. система асимптотически устойчива по Ляпунову, и, кроме того, число жёсткости s:
, т.е. система асимптотически устойчива по Ляпунову, и, кроме того, число жёсткости s: 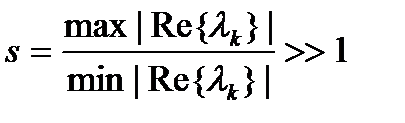 (3)
(3)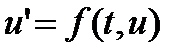 ,
, 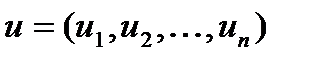 ,
, 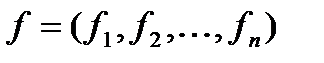 для опр-я жесткости системы вместо A используется м-ца Якоби:
для опр-я жесткости системы вместо A используется м-ца Якоби: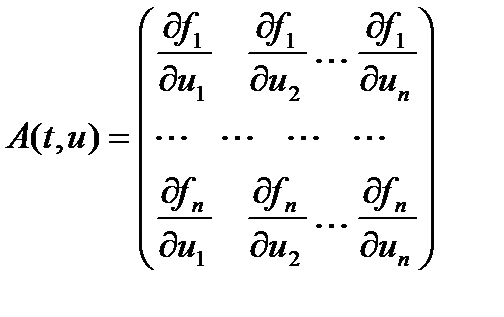
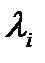 . Общая схема многошагового метода имеет вид
. Общая схема многошагового метода имеет вид 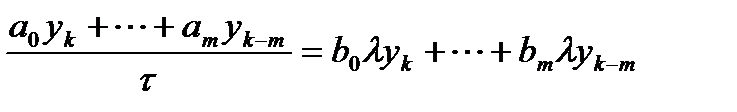 , (4) или
, (4) или 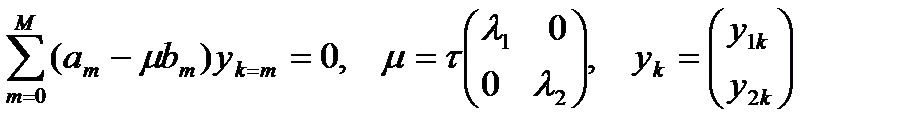 (5)
(5)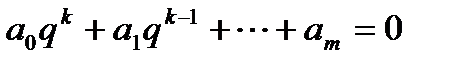 (6) в силу отличия коэфф-в уравнений. Однако, при достаточно малых значениях
(6) в силу отличия коэфф-в уравнений. Однако, при достаточно малых значениях 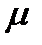 , корни характер-х многочленов (5) и (6) будут близки.
, корни характер-х многочленов (5) и (6) будут близки.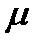 => устойчивость алгоритма не будет зависеть от выбора шага сетки. Область значений параметра
=> устойчивость алгоритма не будет зависеть от выбора шага сетки. Область значений параметра 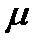 , при которых выполняется условие корней (все корни хар-го многочлена лежат на комплексной плоскости внутри круга единичного радиуса и отсутствуют кратные корни, лежащие на единичной окружности) для разностного уравнения (5) называют областью устойчивости метода.
, при которых выполняется условие корней (все корни хар-го многочлена лежат на комплексной плоскости внутри круга единичного радиуса и отсутствуют кратные корни, лежащие на единичной окружности) для разностного уравнения (5) называют областью устойчивости метода.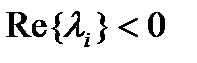 обеспечивает экспоненциальное затухание соответствующей компоненты вектора реш-я (аналит-е реш-е
обеспечивает экспоненциальное затухание соответствующей компоненты вектора реш-я (аналит-е реш-е 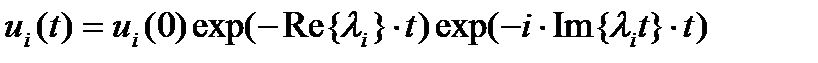 )
) , затухают быстро, и спустя 5-10 шагов перестают сказываться на решении системы в целом. Однако шаг интегрирования должен всегда быть ориентирован на усл-е устойч-ти именно самой "быстрой" компоненты реш-я, ибо неудачный выбор шага может в корне изм-ть ее пов-е.
, затухают быстро, и спустя 5-10 шагов перестают сказываться на решении системы в целом. Однако шаг интегрирования должен всегда быть ориентирован на усл-е устойч-ти именно самой "быстрой" компоненты реш-я, ибо неудачный выбор шага может в корне изм-ть ее пов-е.  .
.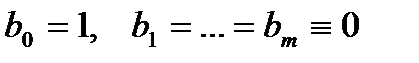 .
.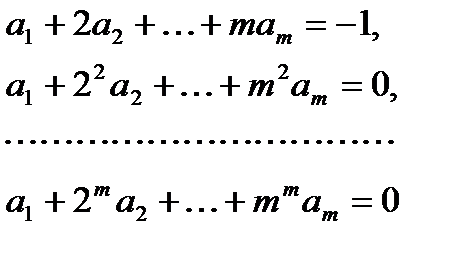
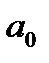 затем выражается следующим образом
затем выражается следующим образом 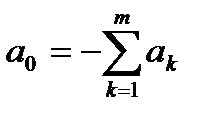 .
.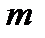 -го. Пр-р одношагового метода Гира – неявная схема Эйлера первого порядка точности
-го. Пр-р одношагового метода Гира – неявная схема Эйлера первого порядка точности