
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Итерационные методы решения систем ЛАУ. Метод простой итерации. Условия сходимости и критерий остановки итераций.
Общая схема больш-ва итерационных методов реш-я СЛАУ где Итерационный метод, в котором для вычисления каждого нового Итерационный процесс (2) приводит к решению задачи (1) ó вып-ся условия: 1. последовательность векторов 2. предел данной последовательности является решением (1). Из 2 => матрица где Для произвольных невырожденных матриц Разнообразие итерационных методов связано с выбором конкретного вида матрицы При (5), в отличие от (2), (3), не нужен явный вид м-цы Метод простой итерации: Стационарный одношаговый итерационный метод вида Теорема. Пусть Доказательство: Спектральная норма симметричной матрицы определяется: Теорема. Пусть Доказательство: Поиска оптимального зн-я итер-го параметра
Несложно заметить, что Скорость сходимости метода простой итерации зависит от отношения
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.197 (0.005 с.) |
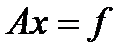 (1) с невырожденной матрицей
(1) с невырожденной матрицей 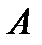 и заданным вектором пр. части
и заданным вектором пр. части  имеет вид
имеет вид 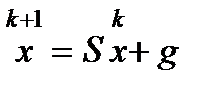 ,
, 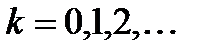 (2)
(2)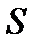 – матрица итерационного метода,
– матрица итерационного метода, 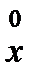 – начальное приближение итерационного процесса. Последоват-ть
– начальное приближение итерационного процесса. Последоват-ть 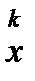 ,
,  используется лишь
используется лишь 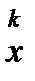 ,
, 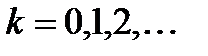 , сходится.
, сходится.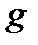 могут быть заданы в виде:
могут быть заданы в виде: 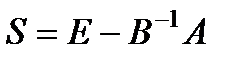 ,
, 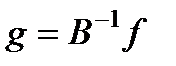 (3)
(3)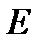 – единичная матрица,
– единичная матрица, 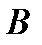 – невырожденная матрица: выполнено условие 1.
– невырожденная матрица: выполнено условие 1.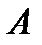 и
и  существует единственное значение вектора
существует единственное значение вектора  такое, что
такое, что 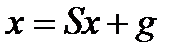 и с учетом выбора (3):
и с учетом выбора (3): 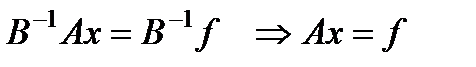
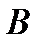 - переобусловливателя. Если матрица
- переобусловливателя. Если матрица 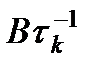 , где
, где 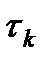 для каждой итерации выбирается из расчета наибольшей скорости сходимости. С точки зрения алгоритмической реализации итерационный процесс (2), (3) удобно представить в виде
для каждой итерации выбирается из расчета наибольшей скорости сходимости. С точки зрения алгоритмической реализации итерационный процесс (2), (3) удобно представить в виде  (5)
(5) и выч-е очередного итерационного приближения сводится к решению СЛАУ:
и выч-е очередного итерационного приближения сводится к решению СЛАУ: 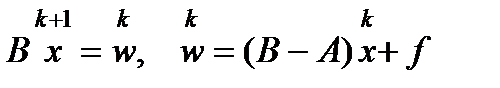 (5')
(5')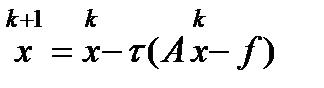 (6). По (2)
(6). По (2) 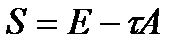 . По (5)
. По (5)  .
.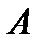 – симметричная положительно определенная матрица
– симметричная положительно определенная матрица 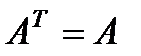 , тогда итерационный метод (6) сходится при
, тогда итерационный метод (6) сходится при 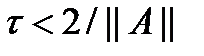 .
.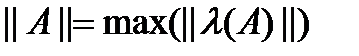 . Если
. Если  . Тогда
. Тогда  . Из положительной определенности матрицы
. Из положительной определенности матрицы  выполняется оценка
выполняется оценка 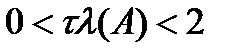 , из которой следует, что
, из которой следует, что  .
. 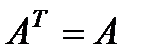 ,
,  , где положит-е постоянные
, где положит-е постоянные 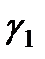 ,
, 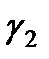 – мин-е и макс-е собственные значения матрицы
– мин-е и макс-е собственные значения матрицы  . Тогда максимальная скорость сходимости итерационного процесса (6) достигается при
. Тогда максимальная скорость сходимости итерационного процесса (6) достигается при 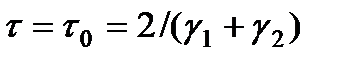 , при этом
, при этом 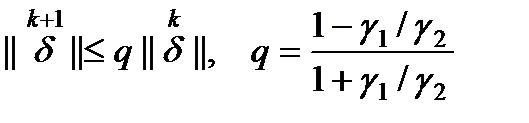 (7)
(7) = определение условия минимума
= определение условия минимума 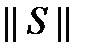 как функции от
как функции от 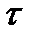 . Найдем явный вид данной функции.
. Найдем явный вид данной функции.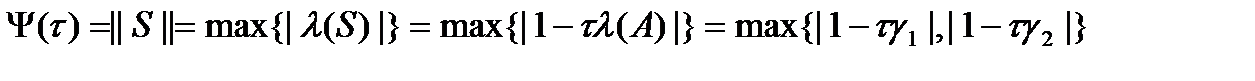 .
.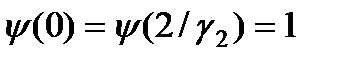 и
и 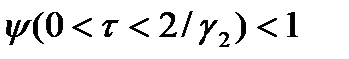 => в интервале значений
=> в интервале значений 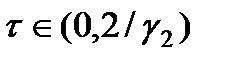 функция
функция 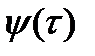 принимает минимальное значение. Поскольку функция
принимает минимальное значение. Поскольку функция 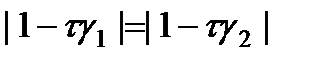 имеет единственный корень на интервале
имеет единственный корень на интервале 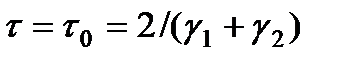 . При этом
. При этом 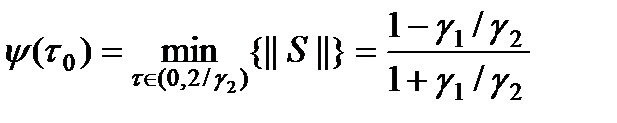 . Теорема доказана.
. Теорема доказана. даже в случае оптимального выбора итерационного параметра. Для симметричных положительно определенных м-ц
даже в случае оптимального выбора итерационного параметра. Для симметричных положительно определенных м-ц 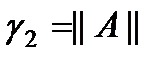 ,
, 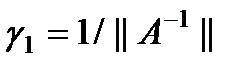 . =>
. => 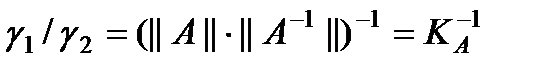 , где
, где  – число обусловленности
– число обусловленности 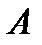 . Для плохо обусловленных матриц (не близко к 1) значение
. Для плохо обусловленных матриц (не близко к 1) значение 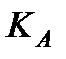 велико, и тогда по (7)
велико, и тогда по (7)  (эфф-ть м-да может ухудшаться при
(эфф-ть м-да может ухудшаться при 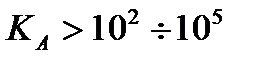 )
)


