
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многошаговые методы. Явные и неявные методы. Метод АдамсаСодержание книги
Поиск на нашем сайте Можно построить численный метод высокого порядка аппроксимации, и при этом будет требоваться вычисление функции правой части только в узлах сетки. Такая задача решена в рамках многошаговых методов. Общая формулировка m - шагового линейного метода имеет вид: где Особенность многошаговых методов состоит в том, что приближенное решение в произвольном Если определены (с достаточной точностью) значения решения в узлах сетки Если Разностные методы вида (1) принято называть явными, подчеркивая тем самым возможность выразить в нем неизвестное решение в явном виде.
Если В этом случае метод называется неявным. Для нахождения неизвестного решения может быть использован какой-либо итерационный метод. Например, итерационный метод Пикара В качестве начального приближения итерационного метода можно использовать известное решение в предыдущем узле сетки:
Метод Адамса: Общая формулировка методов Адамса имеет вид Относительно методов Адамса известно, что для явных методов вида (3) максимальный порядок точности равен N, а для неявных схем с Заметим, что в методе Адамса, в отличие от методов Рунге-Кутты, условие достижения максимального порядка аппроксимации приводит к однозначному определение коэффициентов, а сама задача нахождения коэффициентов схемы аналогична построению интерполяционного полинома заданного порядка. Для явных методов Адамса нахождение неизвестного решения носит характер экстраполяции (приближённое определение значений функции f(x) в точках x, лежащих вне отрезка [x0,xn], по её значениям в точках x0 < x1 <... < xn), что связано с выходом искомого решения за границы интервала, на котором решение и правые части уже вычислены. В силу этого экстраполяционные (явные) методы Адамса имеют меньшую точность и устойчивость по сравнению с неявными. Примером методов Адамса могут быть трех- и четырехшаговые явные методы
Неявный метод Адамса четвертого порядка аппроксимации имеет вид.
Заметим, если правая часть задачи зависит от решения, то для вычисления
|
||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 673; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

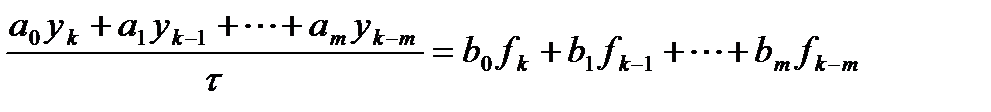 , (0)
, (0)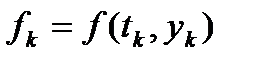 .
. 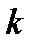 -том узле сетки вычисляется с использованием значений приближенного решения в предыдущих m узлах сетки. Отметим, что начальные условия задачи Коши заданы только в одном узле. Для начала расчетов по (0) нужно получить недостающие m-1 значений решения. Это, например, можно осуществить с помощью формул Р-К или метода Эйлера, но шаг сетки при этом необходимо брать достаточно малым, чтобы погрешность, вносимая в приближенное значение недостающих неизвестных, была сопоставима с ожидаемой погрешностью многошагового метода.
-том узле сетки вычисляется с использованием значений приближенного решения в предыдущих m узлах сетки. Отметим, что начальные условия задачи Коши заданы только в одном узле. Для начала расчетов по (0) нужно получить недостающие m-1 значений решения. Это, например, можно осуществить с помощью формул Р-К или метода Эйлера, но шаг сетки при этом необходимо брать достаточно малым, чтобы погрешность, вносимая в приближенное значение недостающих неизвестных, была сопоставима с ожидаемой погрешностью многошагового метода. 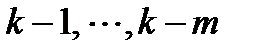 , то уравнение (0) дает рекурсивный алгоритм нахождения приближ-го решения в узлах сетки
, то уравнение (0) дает рекурсивный алгоритм нахождения приближ-го решения в узлах сетки 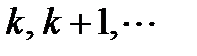 При этом функция правой части в каждом узле сетки вычисляется однократно.
При этом функция правой части в каждом узле сетки вычисляется однократно.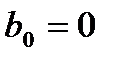 , то
, то 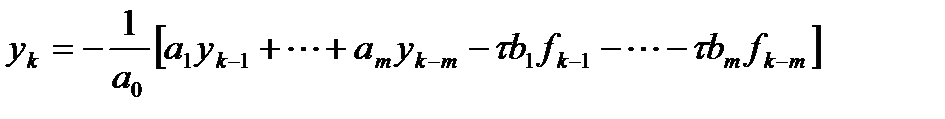 (1)
(1)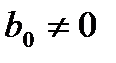 , то решение
, то решение 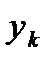 уравнения (0) в общем случае не может быть выражено в явном виде:
уравнения (0) в общем случае не может быть выражено в явном виде: 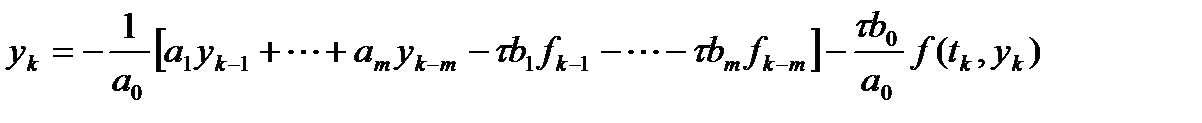 (2)
(2)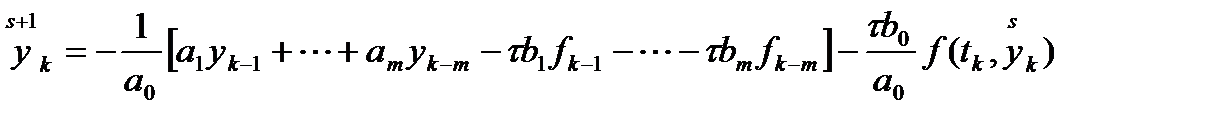 .
.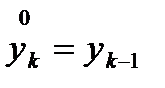 , либо, например, приближение по схеме Эйлера:
, либо, например, приближение по схеме Эйлера: 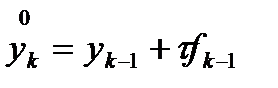 . При достаточно малых шагах сетки такой итерационный процесс сходится и позволяет за 2-3 итерации получить удовлетворительную точность решения. Более высокую скорость сходимости может обеспечить итерационный метод Ньютона.
. При достаточно малых шагах сетки такой итерационный процесс сходится и позволяет за 2-3 итерации получить удовлетворительную точность решения. Более высокую скорость сходимости может обеспечить итерационный метод Ньютона. 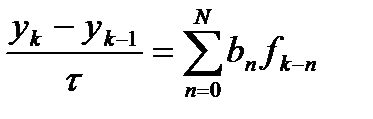 (3)
(3)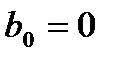
 максимальный порядок аппроксимации равен N+1. Нахождение коэффициентов
максимальный порядок аппроксимации равен N+1. Нахождение коэффициентов 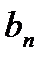 для получения максимального порядка аппроксимации аналогично, как и для методов Рунге-Кутты (обеспечивающие обнуление "возмущающих" слагаемых до максимально возможного порядка малости).
для получения максимального порядка аппроксимации аналогично, как и для методов Рунге-Кутты (обеспечивающие обнуление "возмущающих" слагаемых до максимально возможного порядка малости). , (4)
, (4)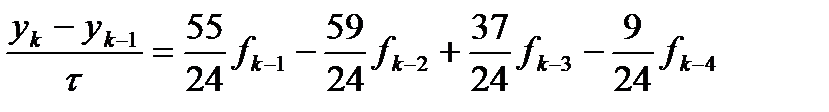 . (5)
. (5)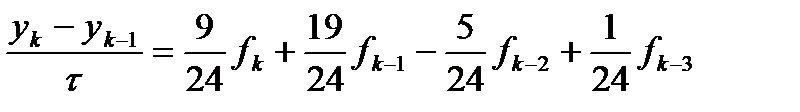 . (6)
. (6)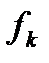 в общем случае требуется использовать неизвестное в данном узле решение
в общем случае требуется использовать неизвестное в данном узле решение 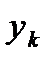 . В итоге, уравнение (6) может оказаться неразрешимым явно относительно искомого решения. Для преодоления указанных трудностей на практике обычно используют комбинацию формул (5) и (6). Формула (5) служит для предсказания решения с пятым порядком точности (погрешность на одном шаге на порядок выше порядка аппроксимации), а схема (6) в силу своей неявности, осуществляет коррекцию приближенного решения с целью повышения устойчивости и точности метода.
. В итоге, уравнение (6) может оказаться неразрешимым явно относительно искомого решения. Для преодоления указанных трудностей на практике обычно используют комбинацию формул (5) и (6). Формула (5) служит для предсказания решения с пятым порядком точности (погрешность на одном шаге на порядок выше порядка аппроксимации), а схема (6) в силу своей неявности, осуществляет коррекцию приближенного решения с целью повышения устойчивости и точности метода. 


