
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Число обусловленности матрицы системы лау. Оценки вычислительной погрешности при решении систем лауСодержание книги
Поиск на нашем сайте Пусть правая часть системы возмущена – задана с абсолютной погрешностью где
Последнее неравенство (3) выражает устойчивость решения по правой части, что эквивалентно требованию ограниченности
Из неравенств (3) и (4) следует оценка относительной погрешности возмущенной задачи:
Согласно (5) погрешность возмущенной задачи пропорционально возрастает с ростом возмущений правой части, причем коэффициент пропорциональности определяется произведением норм матриц характеризующее зависимость относительной погрешности решения СЛАУ от величины относительного возмущения правой части, называется числом обусловленности матрицы. Если число обусловленности матрицы велико, то говорят, что данная матрица плохо обусловлена. Если число обусловленности близко к единице, то матрица считается хорошо обусловленной. Обычно для оценки числа обусловленности используется спектральная норма матриц ( Для плохо обусловленных матриц малая ошибка входных данных приводит к существенному изменению решения; аналогичным образом и для погрешности промежуточных вычислений. Так, например, в процессе приведения матрицы системы к треугольному виду выполняется ряд преобразований ее коэффициентов. В итоге, на этапе обратного хода метода Гаусса решается задача с возмущенными коэффициентами матрицы и полная оценка относительной погрешности должна исходить из следующей возмущенной задачи: Если матрица возмущенной задачи (7) не вырожденная, то возмущения коэффициентов матрицы могут быть соотнесены с возмущениями правой части и вместо задачи (7) достаточно рассмотреть задачу для которой имеет место оценка (5). На практике величина Вектор Оценки числа обусловленности матриц требуют вычисления обратной матрицы или, по крайней мере, оценки максимального и минимального собственных значений в случае симметричных матриц. В силу этого практическая оценка фактической точности приближенного решения системы ЛАУ согласно неравенству (5) представляет собой сложную задачу. Тем не менее, для ряда практически значимых случаев оценка (5) представляется полезной в плане контроля точности вычислений.
|
||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

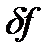 . Тогда фактически вместо
. Тогда фактически вместо  мы решаем возмущенную задачу
мы решаем возмущенную задачу 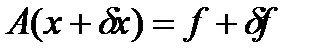 (1)
(1)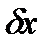 – абсолютная погрешность решения, ассоциированная с возмущением правой части. Погрешность
– абсолютная погрешность решения, ассоциированная с возмущением правой части. Погрешность 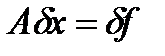 (2)
(2) (3) - норма абс. вел-ны погрешности
(3) - норма абс. вел-ны погрешности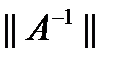 . Из постановки задачи имеем
. Из постановки задачи имеем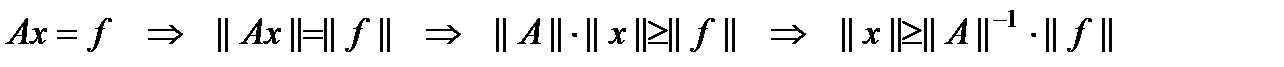 . (4)
. (4)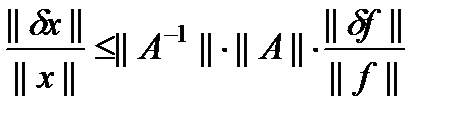 (5)
(5) и
и 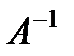 . Число
. Число 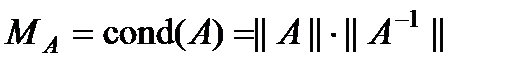 , (6)
, (6) , сингулярные числа матрицы вычисляются как корень из совпадающих собственных значений матриц
, сингулярные числа матрицы вычисляются как корень из совпадающих собственных значений матриц 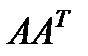 ), которая является подчиненной для евклидовой векторной нормы. Для симметричных матриц число обусловленности определяется отношением модулей наибольшего и наименьшего собственного значения матрицы.
), которая является подчиненной для евклидовой векторной нормы. Для симметричных матриц число обусловленности определяется отношением модулей наибольшего и наименьшего собственного значения матрицы. , (7)
, (7) (8)
(8)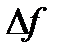 может быть вычислена на основе полученного приближенного решения задачи
может быть вычислена на основе полученного приближенного решения задачи 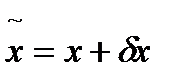 :
: 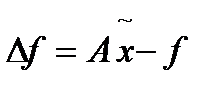 (9)
(9)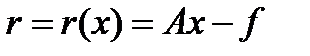 принято называть невязкой решения СЛАУ. Норма данного вектора на практике служит количественной мерой возмущения правой части задачи и используется для оценки погрешности приближенного решения.
принято называть невязкой решения СЛАУ. Норма данного вектора на практике служит количественной мерой возмущения правой части задачи и используется для оценки погрешности приближенного решения.


