Задача 7-к: сложное движение материальной точки

 

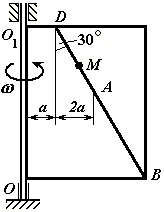
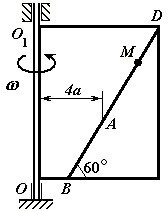
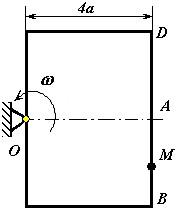
Пластина (рис. 1 – 6) вращается вокруг неподвижной оси с постоянной угловой скоростью , заданной в таблице 1 (при знаке минус направление  противоположно показанному на рисунке). Ось вращения на рис. 1 – 4 перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 5 – 6 ось вращения OO ₁, лежит в плоскости пластины (пластина вращается в пространстве).

 По пластине вдоль прямой BD движется точка М. Закон ее относительного движения задается уравнением s  AM  f  t , (s – в сантиметрах, t – в секундах), приведенным в таблице 1. На всех рисунках точка М показана в положении, при котором s  AM 0(при s 0 точка М находится по другую сторону от точки А).

 Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t ₁ =1 с.

 

 

 

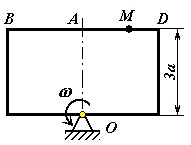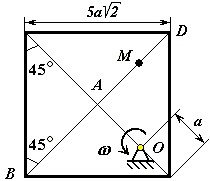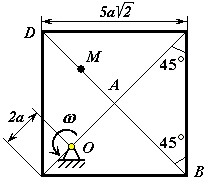
                      Рис. 1                                      Рис. 2                                        Рис. 3

 

 

 

 

                      Рис. 4                                      Рис. 5                                        Рис. 6

 

 

 

 

Таблица 1

№ вар.	, рад/с	а, см	s  AM  f  t , см	№ рис.
1	-2	16	60 t ^43 t ^256	1
2	4	20	60 t ^3 2 t ^2	1
3	3	8	802 t ^2 t ^3	1
4	-4	12	40 t ^23 t 32	1
5	-2	16	60 t ^43 t ^256	2
6	4	20	60 t ^3 2 t ^2	2
7	3	8	802 t ^2 t ^3	2
8	-4	12	40 t ^23 t 32	2
9	-2	16	60 t ^43 t ^256	3
10	4	20	60 t ^3 2 t ^2	3
11	3	8	802 t ^2 t ^3	3
12	-4	12	40 t ^23 t 32	3
13	-2	16	60 t ^43 t ^256	4
14	4	20	40 t 2 t ^240	4
15	3	8	802 t ^2 t ^3	4
16	-4	12	40 t ^23 t 32	4
17	-2	16	60 t ^43 t ^256	5
18	4	20	60 t ^3 2 t ^2	5
19	3	8	802 t ^2 t ^3	5
20	-4	12	40 t ^23 t 32	5
21	-2	16	60 t ^43 t ^256	6
22	4	20	60 t ^3 2 t ^2	6
23	3	8	802 t ^2 t ^3	6
24	-4	12	40 t ^23 t 32	6

 

 

 

Примечание. Задача 7-К – на сложное движение точки. При ее решении движение точки по пластине считать относительным, а вращательное движение самой пластины - переносным и воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить расчеты, следует изобразить точку М на пластине в том положении, в котором нужно определить ее абсолютную скорость (или ускорение), а не в произвольном положении, показанном на рисунках к задаче.

 

 

Пример решения задачи

 

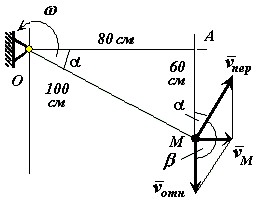
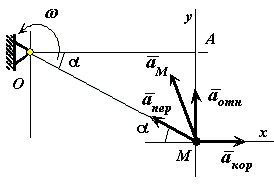
Задача. Прямоугольная пластина вращается вокруг неподвижной оси с постоянной угловой скоростью =4 1/с.  Ось вращения перпендикулярна плоскости пластины и проходит через точку О (рис. 7).

 По пластине вдоль прямой BD движется точка М. Закон ее относительного движения задается уравнением s  AM  f  t  60 t 3  2 t 2; a =20 см; t 1=1 с.

 Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t. 1

Решение. Рассмотрим движение точки как

сложное: v M  v отн  v пер; a M  a отн  a пер  a кор.

7. Определим положение точки: s 1 AM  6012 60 (см. рис. 8).

8. Рассмотрим относительное движение s  AM  f  t  60 t ³ 2 t ².

_отн dsdt ² 4 t ; a _отн  ^ddt ²₂ ^s  606 t  4; v  603 t 

 

Рис. 7

        v 1 603460. см/с; a 1 6064120 см/с

           _отн        ds                                       _отн                                                           ²

dt

9. Рассмотрим переносное движение. Переносное движение это вращение пластины. Найдем расстояние OM. OM  OA ²  AM ² 100 см. 

Переносная скорость точки перпендикулярна отрезку OM и равна v  OM; v  4 100  400 см/с; Переносное ускорение точки пер  пер

       складывается из касательного и нормального:   a _пер  a ^ _пер  a _пер ⁿ    ;  

a ^ _пер  OM  0, так как  const; a _пер ⁿ _²  OM; a _пер ⁿ  4² 100 1600 см/с²  

Ускорение Кориолиса по величине равно a _кор  2 v _отн , a _кор  2604  480 см/с² Направление a _кор найдем повернув вектор v _отн на 90 градусов против часовой стрелки (рис. 9).

           

                                        Рис. 8                                                                 Рис. 9

10. Определим     абсолютную   скорость точки    М.     v _M  v _отн  v _пер.   

v _M  v _отн ²  v _пер ²  2 v _отн  v _пер  cos ; cos   cos  0. 8; v _M 353. 836 см/с

11. Определим абсолютное ускорение точки М. a _M  a _отн  a _пер  a _кор . Введем оси координат xMy. Спроектируем ускорения на эти оси.  

a Mx  a кор  a пер  cos ;	a Mx  800 см/с^2;
a My  a отн  a пер  sin ;	a My 1080 см/с^2;
a M  a Mx 2  a My 2;	a M 1786 см/с^2.

Ответ: v _M 353. 836 см/с; a _M 1786 см/с².

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[1]. Определяем v _B . Направление скорости точки В известно, оно параллельно скорости точки Е, следовательно стержень 2 совершает мгновенно поступательное движение и v _B  v _E 2. 4 м/с (рис. 8).