Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первый закон термодинамики и его применение К изопроцессамСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При анализе работы, проектировании и проведении расчётов тепловых машин, таких как двигатели внутреннего сгорания (ДВС), компрессоры и т.п. возникает необходимость аналитически определять их основные характеристики: мощность, коэффициент полезного действия и ряд других. Рабочим телом в таких устройствах часто является воздух, который совершает работу (ДВС) или над ним совершается работа (компрессор). При этом процессы, происходящие с воздухом или другим газом, являются повторяющимися, т.е. циклическими. Изменения в состоянии рабочего тела можно представить одним из термодинамических процессов: быстрое, т.е. адиабатическое сжатие или расширение, изохорное, изобарное или изотермическое нагревание или охлаждение и т.д. само же рабочее тело может совершать работу (или над ним совершается работа) и участвовать в теплообмене с окружающей средой. Для количественного описания таких процессов широко применяются законы термодинамики и уравнения состояния идеального газа. Допустим, что некоторая система (рабочее тело – газ, заключенный в цилиндр под поршнем), обладая внутренней энергией U 1, получила некоторое количество теплоты Q и, перейдя в новое состояние, с внутренней энергией U 2, совершила работу A над внешней средой. Количество теплоты считается положительным, когда оно подводится к системе, а работа – положительной, когда система совершает ее против внешних сил. Опыт показывает, что в соответствии с законом сохранения энергии при любом способе перехода системы из первого состояние во второе изменение внутренней энергии D U = U 2 – U 1 будет одинаковым и равным разности между количеством теплоты Q, полученным системой, и работой A, совершенной системой против внешних сил: D U = Q – A, или Q = D U + A. (1.1) Уравнение (1.1) выражает первый закон термодинамики: теплота, сообщаемая системе, расходуется на изменение её внутренней энергии и на совершение ею работы против внешних сил. Выражение (1) в дифференциальной форме будет иметь вид d Q = d U + d A, или в более корректной форме d Q = d U + d A, (1.2) где d U – бесконечно малое изменение внутренней энергии системы, d Q – бесконечно малое количество теплоты, d A – элементарная (физически малая) работа. В этом выражении d U является полным дифференциалом (поскольку зависит только от внутреннего состояния рабочего тела), а d Q и d A таковыми не являются, поскольку зависят от вида и хода совершенного над газом процесса. Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К (1 °С):
Единица удельной теплоемкости – джоуль на килограмм-кельвин (Дж/(кг×К)). Молярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:
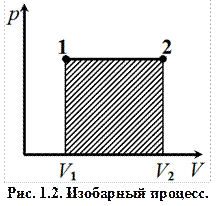
где n = m / M – количества вещества. Различают теплоёмкости при постоянном объёме и постоянном давлении, если в процессе нагревания вещества его объём или давление поддерживается постоянным. Запишем выражение первого закона термодинамики (1.2) для 1 моль газа, используя выражение (1.3) и учитывая, что d A = p d V: C m d T = d U m + p d V m. (1.4) Если газ нагревается при постоянном объёме, то работа внешних сил равна нулю и сообщаемая газу извне теплота идёт только на увеличение его внутренней энергии:
т.е. молярная теплоемкость газа при постоянном объеме CV равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К. Если газ нагревается при постоянном давлении, то выражение (1.4) можно записать в виде
Учитывая, что C p = CV + R, или Cp – CV = R. (1.6) Выражение (1.6) называется уравнением Майера; оно показывает, что Cp всегда больше CV на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется ещё дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Среди равновесных процессов, происходящих с термодинамическими системами, выделяют изопроцессы, при которых один из основных параметров состояния (температура, объем, давление или иные величины) сохраняется постоянным. Рассмотрим кратко основные изопроцессы. Изохорный процесс (V = const). Диаграмма этого процесса (изохора) в координатах (p, V) изображается прямой, параллельной оси ординат (рис. 1.1), где процесс 1 – 2 есть изохорное нагревание, а 1 – 3 – изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т.е. d A = p d V = 0. Из первого закона термодинамики (1.2) для изохорного процесса следует, что вся теплота, сообщаемая газу, идёт на увеличение его внутренней энергии: d Q = d U. Согласно формуле (1.5), d U m = CV d T. Тогда для произвольной массы газа получим
Изобарный процесс (p = const). Диаграмма этого процесса (изобара) в координатах (p, V) изображается прямой, параллельной оси абсцисс (оси V). При изобарном процессе работа газа при увеличении объема от V 1 до V 2 равна
и определяется площадью заштрихованного прямоугольника (рис. 1.2). Если использовать уравнение Клапейрона–Менделеева для двух состояний (1 и 2), то
откуда
Тогда выражение (1.8) для работы изобарного расширения примет вид
В изобарном процессе при сообщении газу массой m количества теплоты
его внутренняя энергия возрастает на величину (согласно формуле (1.5))
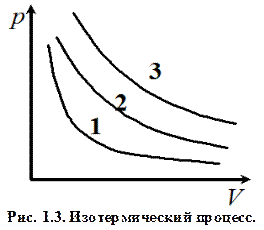
При этом газ совершит работу, определяемую выражением (1.9). Изотермический процесс (T = const). Изотермический процесс совершается при постоянной температуре и описывается законом Бойля–Мариотта: pV = const. Диаграмма этого процесса (изотерма) в координатах (p, V) представляет собой гиперболу (см. рис. 1.3), расположенную тем выше, чем выше температура, при которой происходит процесс (1 – T 1, 2 – T 2, 3 – T 3; T 1 < T 2 < T 3).
Найдём работу изотермического расширения
Так как при T = const внутренняя энергия идеального газа не изменяется:
то из первого закона термодинамики (d Q = d U + d A) следует, что для изотермического процесса d Q = d A, т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил. Следовательно, для того, чтобы при расширении газа температура не понижалась, к газу при изотермическом процессе необходимо подводить количество теплоты, эквивалентное внешней работе расширения. Адиабатическим (или адиабатным) называется процесс, при котором отсутствует теплообмен (d Q = 0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, быстрое сжатие горючей смеси или её быстрое расширение после воспламенения топлива в цилиндрах двигателей внутреннего сгорания, сжатие воздуха в компрессоре (компрессоры для получения сжатого воздуха, компрессоры в холодильных установках и т.п.). Из первого закона термодинамики (d Q = d U + d A) для адиабатного процесса следует, что d A = – d U, (1.10) т.е. работа совершается за счет изменения (уменьшения) внутренней энергии системы (рабочего тела). Используя выражения для работы идеального газа d A = p d V и (1.5) для CV, для произвольной массы газа перепишем уравнение (1.10) в виде
Дифференцируя уравнение состояния идеального газа
Исключим из (1.11) и (1.12) температуру T:
Разделив переменные и учитывая, что отношение Cp / CV = k – величина безразмерная, найдем
Интегрируя это уравнение в пределах от p 1 до p 2 и, соответственно, от V 1 до V 2, а затем, потенцируя, придем к выражению p 2 / p 1 = (V 1 / V 2) k или Так как состояния 1 и 2 выбраны произвольно, то можно записать pV k = const. (1.13) Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона. Для перехода к переменным (T, V) или (T, p) исключим из (1.13) с помощью уравнения Клапейрона–Менделеева
соответственно давление или объем, будем иметь:
Выражения (1.13)–(1.15) представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина k называется показателем адиабаты (или коэффициентом Пуассона). Из курса общей физики (раздел «Термодинамика») известно, что показатель адиабаты может быть задан следующим образом:
здесь i – число степеней свободы, которое зависит от рода газа, точнее от строения его молекул. Для одноатомных газов (He, Ne, Hg – пары ртути и др.), хорошо удовлетворяющих условию идеальности (т.е. достаточно разреженные), i = 3, k = 1,67. Для двухатомных газов (H2, N2, O2 и др.) i = 5, k = 1,4. Для многоатомных газов (с числом атомов три и более, таких как CO2, H2O – пары воды, этан, метан и др.) i = 6, k = 1,33. Поскольку в нашем случае рассматриваемым рабочим телом является воздух в составе которого, как известно, доминируют азот – 78 % и кислород – 21 %, то для него принимается i = 5, k = 1,4. Отметим, что число степеней свободы, проявляющееся в значениях теплоемкостей и, соответственно, влияющее на показатель адиабаты k, у двухатомных газов (и многоатомных) зависит от температуры. Молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы. Поэтому по закону равномерного распределения энергии по степеням свободы для воздуха, как смеси двухатомных газов должно выполняться i = 6, k = 1,33, CV =
Такое поведение теплоемкости объясняется квантованием энергии вращения и колебаний молекул. Вращательная энергия при комнатных температурах уже оказывается «возбужденной» и полностью «включенной», а колебательная начинает возбуждаться только при температурах ~103 К и на полной теплоемкости практически не сказывается при комнатных температурах и даже при нагревании воздуха до температур в несколько сотен °С (как в ДВС). Диаграмма адиабатного процесса (адиабата) в координатах (p, V) изображается гиперболой (рис. 1.5), но идет более круто, чем изотерма. Это объясняется тем, что при адиабатическом сжатии 1–3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.
Вычислим работу, совершаемую газом в адиабатном процессе. Запишем уравнение (1.10) в виде
Если газ адиабатически расширяется от объема V 1 до V 2, то его температура уменьшается от T 1 до T 2 и работа расширения идеального газа
Применяя те же приемы, что и при выводе формулы (1.14), выражение (1.17) для работы при адиабатическом расширении можно преобразовать к виду
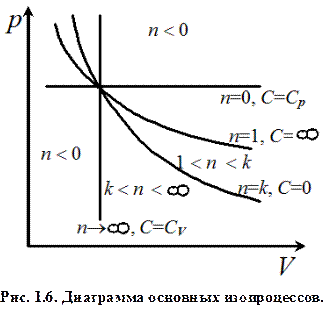
Работа, совершаемая газом при адиабатическом расширении 1–2 (определяется площадью, заштрихованной на рис. 1.5), меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом – температура поддерживается постоянной за счет притока извне эквивалентного количества тепла. Политропный процесс Рассмотренные изохорный, изобарный, изотермический и адиабатный процессы имеют общую особенность – они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны CV и Cp, в изотермическом процессе (d T = 0) теплоемкость равна ± ∞, в адиабатическом (d Q = 0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется политропным. Исходя из первого закона термодинамики при условии постоянства теплоемкости (C = const) можно вывести общее уравнение политропы: pV n = const, (1.18) где n = (C – Cp) / (C – CV) – показатель политропы. Уравнения состояния всех перечисленных выше изопроцессов могут быть формально сведены к уравнению политропы. Сравним изопроцессы и получим для каждого процесса уравнение исходя из уравнения политропы. Чтобы получить уравнение изобары в (1.18) нужно положить n =0 и C = Cp, получим p = const. При n =1 и C = ∞ получаем уравнение изотермы pV = const. При n = k и C =0 получаем уравнение адиабаты pV k = const. Характерное поведение показателя политропы и теплоемкости при переходе от одного процесса к другому можно свести в виде единой диаграммы в координатах (p, V) на рис. 1.6. На диаграмме показано как меняются величины (для двухатомных газов или их смеси, например, воздуха) при переходе от двух характерных прямых: от изобары к изохоре. Двигаясь по часовой стрелке от изобары к изохоре, видим, что показатель политропы растёт и при приближении к изохоре уходит в бесконечность.
Действительно, при увеличении n изобара переходит в гиперболу, идущую всё более и более круто и при очень больших значениях n трансформируется практически в вертикальную линию, поэтому уравнение изохоры получится из (1.18) при n =± ∞ и C = CV. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса. Обратим внимание ещё раз на то, что рассмотренные выше политропные процессы считались равновесными, и количественная теория для их описания дает точные результаты, а также изображать их можно графически, если они таковыми являются. Равновесные процессы – процессы, состоящие из последовательности равновесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало, т.е. реальный процесс, чтобы считать его равновесным должен протекать достаточно медленно, несколько часов или хотя бы несколько минут. Все реальные процессы неравновесны (они протекают с конечной скоростью, а часто очень быстро за малые доли секунды), но в ряде случаев неравновесностью реальных процессов можно пренебречь (чем медленнее процесс протекает, тем он ближе к равновесному). В дальнейшем будем считать рассматриваемые процессы равновесными или точнее, квазиравновесными. Как было сказано выше, в тепловых машинах рабочее тело совершает повторяющийся или, точнее, круговой циклический процесс. Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное состояние. На диаграмме процессов цикл изображается замкнутой кривой (рис. 1.7). Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1 – а – 2) и сжатия (2 – b – 1) газа. Работа расширения (определяется площадью фигуры 1 a 2 V 2 V 1 1) положительна (d V > 0), работа сжатия (определяется площадью Если за цикл совершается положительная работа
Прямой цикл используется в тепловых двигателях – периодически действующих двигателях, совершающих работу за счет полученной извне теплоты. Обратный цикл используется в холодильных машинах – периодически действующих установках, в которых за счет работы внешних сил теплота переносится от рабочего тела к телу с более высокой температурой (в окружающую среду). В результате кругового процесса система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии равно нулю. Поэтому первый закон термодинамики (1.1) для кругового процесса Q = D U + A = A, (1.19) т.е. работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому Q = Q 1 – Q 2, Q 1 – количество теплоты, полученное системой, Q 2 – количество теплоты, отданное системой. Поэтому термический коэффициент полезного действия для кругового процесса
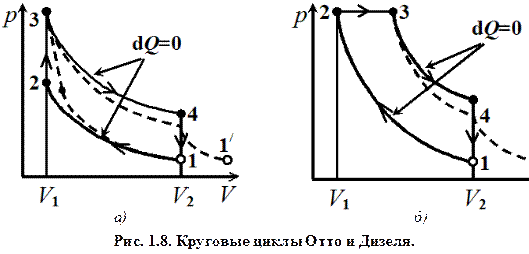
Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении. Причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым. Любой равновесный процесс является обратимым. Обратимость равновесного процесса, происходящего в системе, следует из того, что ее любое промежуточное состояние есть состояние термодинамического равновесия; для него «безразлично», идет в прямом или обратном направлении. Реальные процессы сопровождаются диссипацией энергии (из-за трения, теплопроводности, потери части рабочего тела из-за негерметичности цилиндров, например, и т.д.). Обратимые процессы – это идеализация реальных процессов. Их рассмотрение важно по двум причинам: 1) многие процессы в природе и технике практически обратимы; 2) обратимые процессы являются наиболее экономичными; имеют максимальный термический коэффициент полезного действия, что позволяет указать пути повышения к.п.д. реальных тепловых двигателей. В заключение в качестве примера приведем два круговых процесса, моделирующих работу реальных тепловых ДВС: цикл Отто (рис. 1.8, а) и цикл Дизеля (рис. 1.8, б). Цикл Отто представляет собой идеальную модель процессов, происходящих с воздухом в цилиндре бензиновых двигателей, Дизеля – дизельных двигателей внутреннего сгорания.
Так в бензиновом двигателе идеальный круговой процесс изображается замкнутой кривой 1 – 2 – 3 – 4. После забора новой порции горючей смеси (1) происходит адиабатическое ее сжатие 1 – 2, затем изохорное нагревание 2 – 3, рабочий ход – адиабатное расширение 3 – 4, и возвращение в исходную точку 4 – 1, для того, чтобы замкнуть цикл. В реальном двигателе после забора свежей порции горючей смеси происходит сжатие, но незначительное количество теплоты теряется и процесс идет чуть выше, чем по адиабате. Далее воспламенение происходит немного раньше прихода поршня в верхнюю мертвую точку (опережение зажигания), затем расширение снова чуть ниже, чем по адиабате. Расширение отработанной горючей смеси происходит в атмосферу после открытия выпускного клапана 4 – 1 /. Поэтому реальные процессы изображены пунктирными линиями. Реальные процессы, происходящие внутри двигателя, будет правильнее считать политропными: 1 – 2 – политропа, близкая к адиабате, 2 – 3 – политропа, близкая к изохоре и т.д. Аналогично можно рассмотреть процессы для цикла Дизеля (предлагаем сделать это упражнение самостоятельно).
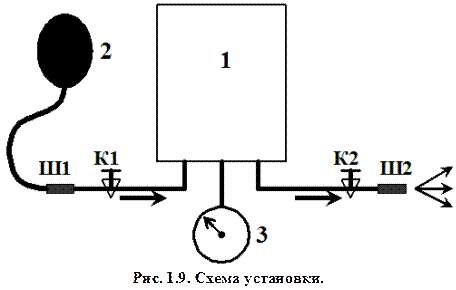
Лабораторная установка Принципиальная схема лабораторной установки представлена на рис. 1.9. В состав установки входит бак 1 (банка объемом 3 литра). Нагнетание воздуха в бак производится при помощи груши-помпы 2, через штуцер Ш1 при открытии крана К1. Для измерения избыточного давления в баке служит мембранный манометр 3. Стравливание воздуха в атмосферу производится через штуцер Ш2 при открытии крана К2.
Параметры состояния атмосферного воздуха в аудитории во время проведения опыта контролируются термометром и барометром.
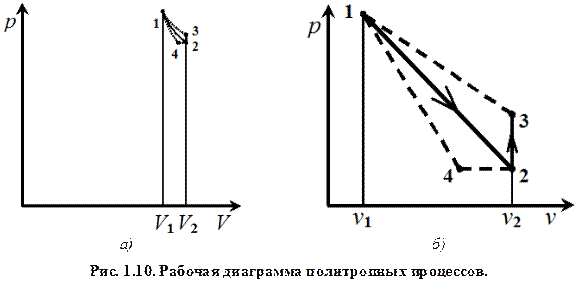
Выполнение работы 2.1. С помощью груши-помпы (открыв кран К1) провести нагнетание воздуха в бак до избыточного давления 60...120 мм рт. ст. (по указанию преподавателя). Сжатие воздуха сопровождается его нагревом, поэтому после нагнетания сделать выдержку 3-4 минуты, необходимую для выравнивания температур воздуха в баке и окружающей среды. При достижении установившихся показаний манометра величину избыточного давления Р 1 изб занести в табл.1.1. 2.2. Осуществить политропное расширение воздуха от начального давления Р 1 = Р 1 изб + Р атм до давления Р 2 = Р атм. + 20 мм.рт.ст. (Р 2 изб = 20 мм.рт.ст.). Для этого приоткрыть кран К2 и удерживать его до тех пор (3–6 сек), пока избыточное давление в баке не упадет до Р 2 изб = 20 мм.рт.ст. После завершения расширения кран должен быть немедленно закрыт. Процесс расширения воздуха сопровождается понижением температуры в баке и одновременно подводом теплоты от относительно более горячей окружающей среды. На P - V диаграмме, представленной на рис.1.10, этот процесс изображен линией 1-2. 2.3. Выждать время, необходимое для прогрева воздуха, оставшегося в баке, до комнатной температуры (2-3 минуты). Нагрев в изохорных условиях сопровождается подводом к воздуху теплоты и возрастанием избыточного давления в баке. На диаграмме состояния этот процесс изображен линией 2-3. После установления показаний манометра значение Р 3 изб занести в табл.1.1.
2.4. Замерить и занести в табл.1.1 значения параметров атмосферного воздуха в лаборатории. Таблица 1.1. Результаты эксперимента
|
||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.68.161 (0.015 с.) |
|||||||||||||||||

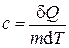 .
.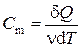 , (1.3)
, (1.3)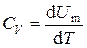 , (1.5)
, (1.5)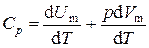 .
.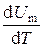 не зависит от вида процесса (внутренняя энергия идеального газа не зависит от p, ни от V, а определяется лишь температурой T) и всегда равна CV (см. (1.5)), и, дифференцируя уравнение Клапейрона–Менделеева pV m = RT по T (при p = const), получаем
не зависит от вида процесса (внутренняя энергия идеального газа не зависит от p, ни от V, а определяется лишь температурой T) и всегда равна CV (см. (1.5)), и, дифференцируя уравнение Клапейрона–Менделеева pV m = RT по T (при p = const), получаем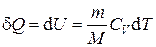 . (1.7)
. (1.7)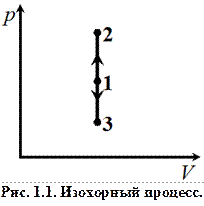
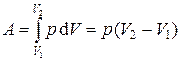 (1.8)
(1.8)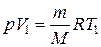 ,
, 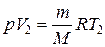 ,
,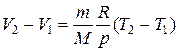 .
.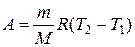 . (1.9)
. (1.9)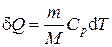
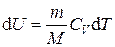 .
.
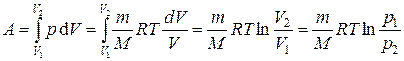 .
.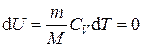 ,
,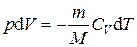 . (1.11)
. (1.11)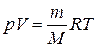 , получим
, получим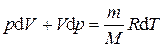 . (1.12)
. (1.12)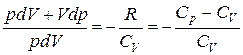 .
.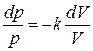 .
.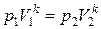 .
.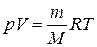
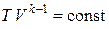 , (1.14)
, (1.14)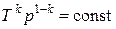 , (1.15)
, (1.15)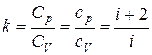 , (1.16)
, (1.16) R. Экспериментальное исследование молярной теплоемкости CV водорода (рис. 1.4) показало, что CV =
R. Экспериментальное исследование молярной теплоемкости CV водорода (рис. 1.4) показало, что CV = 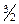 R при низкой температуре (до»50 К), при комнатной CV =
R при низкой температуре (до»50 К), при комнатной CV = 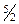 R, и при очень высокой (~104 К) CV =
R, и при очень высокой (~104 К) CV = 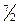 R. Аналогично зависят от температуры теплоемкости азота и кислорода.
R. Аналогично зависят от температуры теплоемкости азота и кислорода.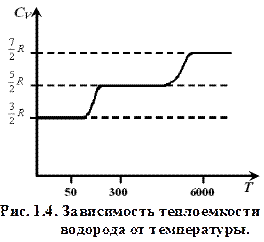
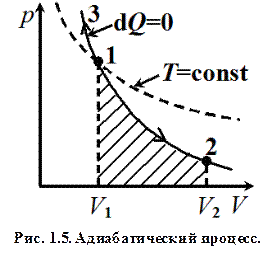
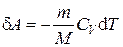 .
.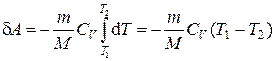 . (1.17)
. (1.17)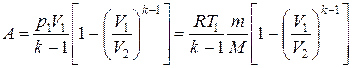 .
.
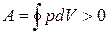 (цикл протекает по часовой стрелке), то он называется прямым (рис. 1.7, a), если за цикл совершается отрицательная работа
(цикл протекает по часовой стрелке), то он называется прямым (рис. 1.7, a), если за цикл совершается отрицательная работа 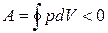 (цикл протекает против часовой стрелки), то называется обратным (рис. 1.7, б).
(цикл протекает против часовой стрелки), то называется обратным (рис. 1.7, б).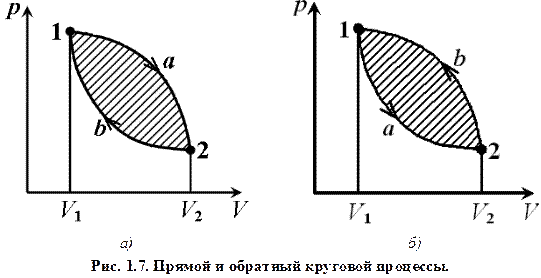
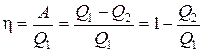 . (1.20)
. (1.20)