Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический анализ процессовСодержание книги Поиск на нашем сайте
На рабочей диаграмме (рис.1.10 б), кроме экспериментально выполненных процессов политропного расширения 1-2 и изохорного нагрева 2-3 построить графики процессов адиабатного расширения воздуха 1-4, изобарного нагрева при атмосферном давлении 4-2 и изотермического сжатия 3-1. Перед построением графиков определить для характерных точек процессов параметры состояния воздуха, а также его массу и занести их в табл.1.2 (вычисления проводить с точностью до трех знаков после запятой). При расчетах использовать уравнение состояния идеального газа принимая значение удельной газовой постоянной воздуха R= 287 Дж/(кг ×К). Для нахождения параметров точки 4 использовать уравнение адиабатного
Для воздуха, как смеси двухатомных газов, принять значение показателя адиабаты k = 1,4. Таблица 1.2. Параметры состояния воздуха
По найденным значениям параметров состояния построить рабочую диаграмму пяти термодинамических процессов. Построение провести на миллиметровой бумаге. При выборе масштабов учитывать реальный диапазон изменения параметров. В силу малости относительного изменения параметров состояния (рис.1.10, а) допускается представить все процессы отрезками прямых линий (рис.1.10, б). Определение показателя политропы Показатель политропы процесса 1-2 вычисляется из уравнения Расчет энергетических характеристик Для всех пяти процессов, изображенных на диаграмме, вычислить массовую теплоемкость воздуха с j, количество теплоты Q, изменение внутренней энергии D U, а также работу деформации A термодинамической системы. Для нахождения изохорной и изобарной теплоемкостей использовать уравнение Майера
и соотношение
В процессах, протекающих с переменной массой, использовать ее среднее значение. Результаты расчетов свести в табл. 1.3. Таблица 1.3. Энергетические характеристики процессов
Изменение внутренней энергии вычисляется, используя выражение
Работа, совершенная газом в процессе может быть найдена как площадь трапеции, ограниченной линией процесса и вертикальными линиями, проходящими через крайние точки процесса (рис. 1.10, б), с пересчетом приведенного объема на реальный. Поэтому процессы представляются отрезками прямых линий. Например, работу совершенную в адиабатическом процессе 1 – 4 проще найти, не используя выражение
а следующим образом:
Точно так же определяется работа в процессах 1 – 2 и 1 – 4. Теплоемкость для политропного процесса определяется по выражению
3. Контрольные вопросы и дополнительные задания 1. Что такое теплоемкость газа? Какая из теплоемкостей – cV или cp –больше и почему? 2. Показатель политропы n > 1. Нагревается или охлаждается идеальный газ при сжатии? 3. Чем отличаются обратимые и необратимые процессы? Почему все реальные процессы необратимы? 4. Изобразить термодинамические процессы в тепловой диаграмме (T-s). 5. Указать на диаграммах точку, соответствующую состоянию воздуха в аудитории во время проведения опыта. 6. Рассчитать плотность воздуха в аудитории во время проведения опыта. 7. Определить массу воздуха, закачанного в бак перед расширением. 8. Найти массу воздуха, который дополнительно вытек бы из бака, если после политропного расширения кран оставить открытым. 9. Изобразить на рабочей диаграмме процесс нагнетания воздуха в бак. 10. Изобразить на тепловой диаграмме процесс нагнетания воздуха в бак. 11. До какой температуры нагрелся бы воздух в баке, если процесс нагнетания той же массы воздуха произвести мгновенно? 12. Какое давление было бы в баке, если процесс нагнетания той же массы воздуха произвести мгновенно? 13. До какой температуры нужно было бы нагреть воздух в баке при закрытом кране для достижения давления Р 1, если начальное состояние его соответствует атмосферным условиям? 14. Вычислить термический КПД цикла 1-3-2-4-1.
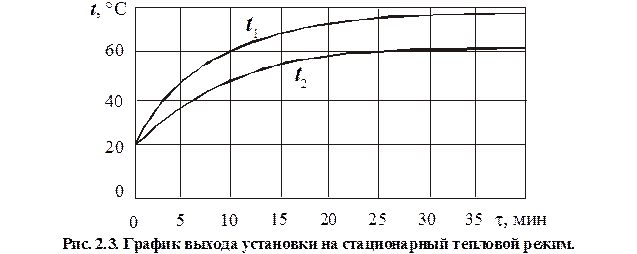
Лабораторная работа № 2 Цель работы: 1. Провести экспериментальные измерения средних температур внутренней и наружной поверхности образца в динамике его нагрева. 2. Построить график выхода установки на стационарный тепловой режим. 3. Для условий стационарного теплового поля рассчитать численное значение коэффициента теплопроводности испытуемого материала.
Оборудование и материалы: лабораторная установка для определения коэффициента теплопроводности
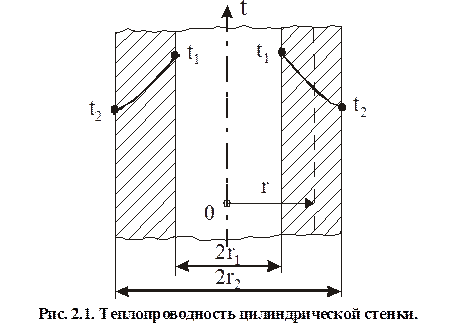
Теоретические сведения Рассмотрим стационарный процесс теплопроводности в цилиндрической стенке (трубе) с внутренним диаметром d 1 = 2 r 1 и наружным диаметром d 2 = 2 r 2 (см. рис. 2.1).
На поверхности стенки заданы постоянные температуры t 1 и t 2. В заданном интервале температур коэффициент теплопроводности материала стенки λ является постоянной величиной. Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее. Дифференциальное уравнение теплопроводности для этой задачи будет иметь вид:
При этом ось 0 z совмещена с осью трубы. При заданных условиях температура изменяется только в радиальном направлении, и температурное поле будет однородным, поэтому
C учетом (2.2) уравнение теплопроводности (2.1) будет иметь вид:
Граничные условия: В результате решения уравнения (2.3) с учетом граничных условий (2.4) получим Для нахождения количества теплоты, проходящего через цилиндрическую поверхность площадью F в единицу времени, можно воспользоваться законом Фурье: Поскольку где Q измеряется в ваттах [Вт].
Таким образом, количество теплоты, проходящее через цилиндрическую стенку в единицу времени полностью определяется заданными граничными условиями и не зависит от радиуса. Тепловой поток Q может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности. При этом расчетные формулы для плотности теплового потока, Вт/м2, принимают вид: (тепловой поток через единицу внутренней поверхности); (тепловой поток через единицу наружной поверхности); (поток теплоты, проходящей через единицу длины трубы). Тепловой поток, отнесенный к единице длины трубы, измеряется в Вт/м и называется линейной плотностью теплового потока. Плотность теплового потока q 1 и q 2 в случае передачи теплоты через трубу неодинаковы, причем всегда q 1 > q 2. Связь между q 1, q 2 и ql следующая: Выражение (2.7) может быть положено в основу методики определения коэффициента теплопроводности любого твердого материала. Так если взять достаточно длину трубу так, чтобы ее длина была значительно больше ее диаметра, поместить внутри по ее оси нагреватель, мощностью W, испытуемый материал нанести в виде цилиндрического слоя, то можно считать, что все выделенное нагревателем тепло проходит через цилиндрический слой материала наружу, а незначительной потерей тепла через торцевые поверхности цилиндра можно пренебречь, поскольку они составляют доли процента от тепла, отданного нагревателем. Тогда можно считать, что Q = W, и из (2.7) получаем
или, учитывая, что r 2/ r 1 = d 2/ d 1, окончательно будем иметь
Таким образом, измерив температуры в стационарном режиме на внутренней и наружной поверхностях цилиндрического слоя, можем определить его коэффициент теплопроводности по выражению (2.12).
Лабораторная установка В лабораторной установке испытуемый материал 6 (паронит) нанесен в виде цилиндрического слоя на металлическую трубку 7 (рис.2.2). Внутри трубы смонтирован электрический нагреватель 8 (ТЭН), выделяющей тепло (неравномерно) по длине трубы. Количество тепла Q, которое выделяется нагревателем и передается через слой материала в окружающую среду, при стационарном тепловом режиме можно определить по мощности W, потребляемой электронагревателем: Q = W. Мощность нагревателя регулируется автотрансформатором 12 и измеряется ваттметром 13. Для измерения температур на наружной и внутренней поверхностях слоя 6 установлены пять пар хромель-копелевых термопар 1 – 5, 1 / – 5 /. Все они через тумблер ВНУТР/НАРУЖ и переключатель 9 поочередно коммутируются с цифровым милливольтметром 10. Общий холодный спай термопар соединен с металлической пластиной 11, имеющей комнатную температуру. Перевод показаний милливольтметра в градусы Цельсия осуществляется с помощью справочной таблицы термопары (приложение 1), с учетом комнатной температуры.
Порядок выполнения работы 2.1. Включить установку и установить мощность нагревателя согласно указаниям преподавателя или лаборанта. На милливольтметре выбрать предел измерений 200 мВ (200m). 2.2. Периодически, с интервалом в 5 минут, контролировать тепловое состояние испытуемого образца путём регистрации показаний термопар и вычисления средних температур внутренней и наружной поверхности. Момент включения установки (начала замеров) считать начальным τ = 0. Результаты измерений заносить в табл.2.1. Процесс нагрева образца иллюстрировать построением графика изменения температур поверхностей с течением времени (рис.2.3). Измерения продолжать до установления стационарного теплового режима, когда прекратится изменение температуры поверхностей со временем (на графике это будет выражаться выходом кривых на горизонтальный участок). При измерении термоЭДС термопар рекомендуется снимать показания в прямом и обратном порядке т.е. ВНУТР: 1-2-3-4-5, а затем НАРУЖ: 5-4-3-2-1. При таком порядке выключатель будет возвращаться в исходное положение 1 и будут исключены лишние ненужные переключения. После снятия показаний во избежание потери времени рекомендуется сразу же определить, используя приложение 1, перепады температур и средние температуры внутренней и наружной поверхностей. Температуры необходимо усреднять, поскольку температура нагревателя не является равномерной. Ориентировочное время выхода установки на стационарный режим до 1 часа. Таблица 2.1. Результаты измерений температур испытуемого материала
2.3. Выключить лабораторную установку. 2.4. По среднему значению температур на внутренней и внешней поверхности испытуемого слоя в стационарном режиме и значению мощности нагревателя вычислить коэффициент теплопроводности материала по формуле
где l – коэффициент теплопроводности испытуемого материала; l – длина трубы, м; d 1 и d 2 – внутренний и наружный диаметры цилиндрического слоя, м; t 1 и t 2 – средние температуры внутренней и наружной поверхностей цилиндрического слоя материала °С. 2.5. По вычисленному значению коэффициента l дать характеристику теплопроводящих (теплоизоляционных) свойств испытуемого материала. Теплоизоляционными материалами считаются материалы, у которых l<0,25 Вт/(м×К). Используя справочные данные (приложение 3) указать материалы, аналогичные испытуемому по теплопроводящей способности.
3. Контрольные вопросы и дополнительные задания 1. Построить график радиального распределения температуры t = f (r) в слое испытуемого материала. Значения температур в промежуточных точках графика (не менее трех точек) рассчитать, пользуясь формулой изменения температуры в однородной цилиндрической стенке при стационарном режиме. 2. Рассчитать термическое сопротивление цилиндрического слоя испытуемого материала. 3. Вычислить линейную плотность теплового потока ql (погонный тепловой поток). 4. Построить график радиального распределения температуры в безразмерном виде. Безразмерные значения радиуса и температуры определяются по формулам:
5. Рассчитать значение градиента температур на внутренней (r = r 1) и внешней (r = r 2) поверхностях слоя материала. 6. Построить график радиального распределения градиента температур. 7. Вычислить значение плотности теплового потока на внутренней (r = r 1) и внешней (r = r 2) поверхностях цилиндрического слоя материала. 8. Построить график изменения плотности теплового потока по толщине цилиндрической стенки. 9. Изобразить картину изотермических линий в сечении испытуемого цилиндрического образца. Показать векторы теплового потока и градиента температуры. 10. Показать вывод расчетной формулы (2.12) для определения коэффициента теплопроводности методом трубы. 11. Привести расчётную формулу для определения коэффициента теплопроводности методом плоского слоя. Лабораторная работа № 3 Цель работы: 1. Провести теплотехнические измерения для определения коэффициента теплоотдачи горизонтальной трубы при свободном движении воздуха для нескольких режимов нагрева (количество режимов задаётся преподавателем). 2. Обобщить результаты эксперимента с использованием теории подобия.
Оборудование и материалы: лабораторная установка для изучения конвективной теплоотдачи
Теоретические сведения Основной задачей теории конвективного теплообмена является определение коэффициента теплоотдачи. Величина теплового потока при конвективном теплообмене определяется формулой Ньютона: Q к = a·D t · А, (3.1) где Q к – конвективная составляющая теплового потока, Вт; a – коэффициент теплоотдачи, Вт/(м2×К); А - площадь теплоотдающей поверхности, м2; D t = t ст– t cр– температурный напор, °С; t ст – средняя температура поверхности тела, °С; t ср – температура теплоносителя (окружающей среды), °С. Теория конвективного теплообмена позволяет определить коэффициенты теплоотдачи для подобных случаев теплообмена путем обобщения экспериментальных данных. Для этого применяются критериальные числа подобия: · критерий Нуссельта, характеризующий интенсивность конвективного теплообмена Nu = a d / l, (3.2) где l – коэффициент теплопроводности окружающей среды, Вт/(м×К); d – характерный геометрический размер теплоотдающей поверхности, который для горизонтально расположенной трубы принимается равным наружному диаметру (d = d), а для вертикально расположенной ее длине (d = l), м; · критерий Грасгофа, характеризующий интенсивность и режим свободного движения
где g – ускорение свободного падения, м/с2; b – коэффициент объемного расширения, который для газов может быть определен из закона Гей–Люссака в виде b = 1 /(t cр+273),K -1; n – кинематическая вязкость окружающей среды, м2/с; · критерий Прандтля, характеризующий соотношение механических (вязкостных) и тепловых свойства теплоносителя Pr = n / а, (3.4) где а – коэффициент температуропроводности окружающей среды, м2/с. Применение теории подобия позволяет обобщить результаты экспериментальных исследований теплоотдачи в виде критериальных уравнений для
Эмпирические коэффициенты c и n, входящие в уравнение (5), определяются путем статистической обработки многочисленных экспериментальных данных. Для теплоотдачи с поверхности горизонтальной трубы при свободной конвекции в диапазоне величин 5×102 < Grж×Prж < 2×107 эти коэффициенты имеют постоянные значения: c = 0,5; n = 0,25, а критериальное уравнение теплоотдачи принимает следующий вид:
Практическое использование эмпирических уравнений подобия заключается в нахождении коэффициентов теплоотдачи по значению
Лабораторная установка
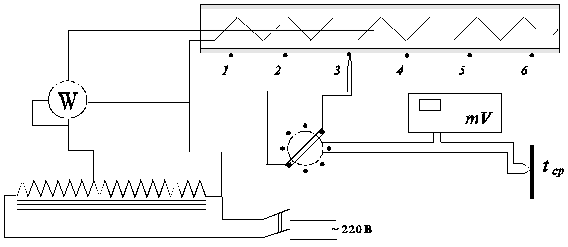
Рис. 3.1. Схема установки | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Теплоотдающей поверхностью в опытах по определению коэффициента теплоотдачи конвективного теплообмена служит поверхность металлической трубы (рис. 3.1).
Внутри трубы, установленной на стойках, находится электрический нагреватель, мощность которого регулируется автотрансформатором и измеряется ваттметром. Мощность нагревателя W в условиях стационарного теплового режима равна полному тепловому потоку Q полн с поверхности нагретой трубы в окружающую среду.
Теплотехнические измерения на данной лабораторной установке включают в себя измерения тепловых потоков и температур. Для определения температуры стенки трубы на ее наружной поверхности закреплены измерительные спаи шести хромель-копелевых термопар.
Общий контрольный спай термопар поддерживается при комнатной температуре. Таким образом, термоЭДС каждой термопары, измеряемая миливольтметром, соответствует разности температур поверхности трубы и окружающей среды t ср. Для перевода милливольт термоЭДС в градусы Цельсия используется справочная таблица термопары (приложение 1). Средняя температура поверхности трубы t ст определяется как средняя арифметическая по показаниям шести термопар.
Порядок выполнения работы
2.1. При участии преподавателя установить мощность нагревателя. Измерить и записать в таблицу 3.1 температуру окружающей среды. На милливольтметре выбрать предел измерений 200 мВ (200m).
2.2. С интервалом в пять минут проводить замеры мощности и температуры, при этом переключатель термопар поочередно подключать к каждой из шести термопар. Результаты измерения температур заносить в таблицу 3.1, определять среднеарифметическую температуру поверхности трубы t ст, а также строить график зависимости t ст от времени. Измерения проводить до установления стационарного теплового режима, при котором средняя температура поверхности трубы не изменяется с течением времени.
2.3. Определить конвективную составляющую теплового потока Q к как разность: Q к = Q полн – Q изл,
где Q изл – поток излучения с поверхности трубы. В соответствии с законом Стефана-Больцмана он определяется по формуле:
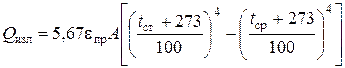 ,
,
где eпр – приведенная степень черноты излучающей поверхности трубы в условиях эксперимента (конкретное значение для исследуемой поверхности выбрать из приложения 2).
2.4. Вычислить коэффициент теплоотдачи, используя формулу (3.1).
2.5. Вычислить критерии Нуссельта (3.2), Грасгофа (3.3). Численное значение критерия Прандтля и теплофизические свойства воздуха выбрать по температуре окружающей среды из приложения 4. Полученные значения занести в таблицу 1.
2.6. Эксперимент повторить для 2-3 режимов нагрева, отличающихся мощностью нагревателя с заполнением таблиц результатов.
Таблица 3.1 Результаты измерения температур на поверхности трубы
| Время, мин | Показания термопар, мВ/D t | D t, °С | t ст, °С | W, Вт | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||||
| 0 |
| |||||||||
| 5 |
| |||||||||
| 10 |
| |||||||||
| 15 |
| |||||||||
| 20 |
| |||||||||
| 25 |
| |||||||||
| 30 |
| |||||||||
| 35 |
| |||||||||
| 40 |
| |||||||||
| 45 |
| |||||||||
| 50 |
| |||||||||
| 55 |
| |||||||||
| 60 |
| |||||||||
| … |
| |||||||||
| d = | l = | eпр = | ||||||||
| t ср = | Q к = | a = | ||||||||
| Pr = | Gr = | NuЭ = | ||||||||
| Примечание. Через косую черту пишется температурный перепад, соответствующий термоЭДС, например | 3,6 54 |
|
| Поделиться: |

 ,
,  ,
,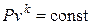 в виде
в виде 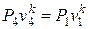 .
. с учётом изотермичности процесса 1-3 (v 1/ v 3 = P 3/ P 1) и равенства объёмов изохорного процесса 2-3 (v 2 = v 3) по формуле
с учётом изотермичности процесса 1-3 (v 1/ v 3 = P 3/ P 1) и равенства объёмов изохорного процесса 2-3 (v 2 = v 3) по формуле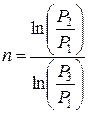 .
.
 .
. .
.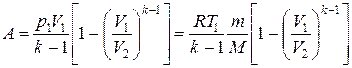 ,
,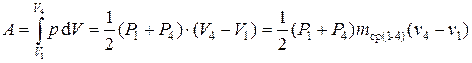 .
.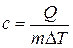 .
.
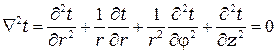 . (2.1)
. (2.1)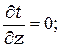
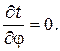 (2.2)
(2.2)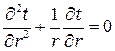 . (2.3)
. (2.3)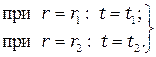 (2.4)
(2.4)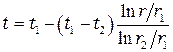 . (2.5)
. (2.5)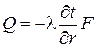 .
.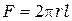 , то
, то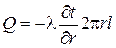 , (2.6)
, (2.6)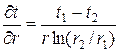 ,
,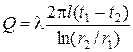 . (2.7)
. (2.7)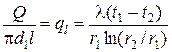 , (2.8)
, (2.8)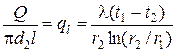 , (2.9)
, (2.9)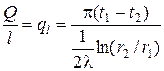 , (2.10)
, (2.10)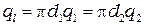 . (2.11)
. (2.11)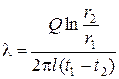 ,
,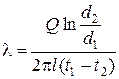 . (2.12)
. (2.12)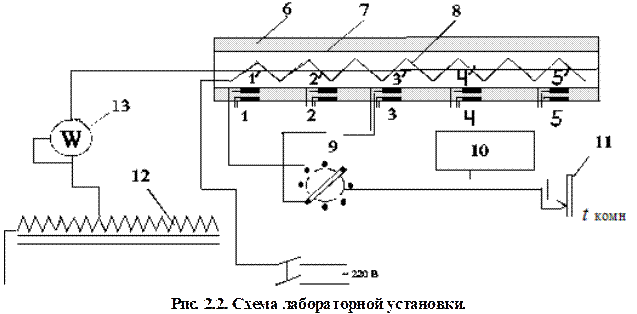
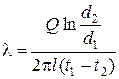 ,
,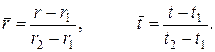
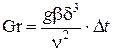 , (3.3)
, (3.3)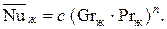 (3.5)
(3.5)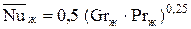 . (3.6)
. (3.6)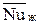 , вычисленному из критериального уравнения для данного класса явлений.
, вычисленному из критериального уравнения для данного класса явлений.