
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Водяной пар. Фазовые переходыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Попытки ряда ученых (Ван-дер-Ваальса, Клаузиуса и других) уточнить уравнения состояния реальных газов путем введения поправок в уравнения состояния для идеальных газов не увенчались успехом, так как эти поправки относились только к объему и силам сцепления между молекулами реального газа и не учитывали ряд других физических явлений, происходящих в этих газах. Поэтому важную роль играет уравнение, предложенное Ван-дер-Ваальсом в 1873 году: Являясь приближенным при количественных расчетах, уравнение Ван-дер-Ваальса качественно хорошо отображает физические особенности газов, так как позволяет описать общую картину изменения состояния вещества с переходом его в отдельные фазовые состояния. В этом уравнении а и b для данного газа являются постоянными величинами, учитывающими: первая - силы взаимодействия, а вторая - размер молекул. Для реальных газов с повышенной плотностью приемлемая точность указанного уравнения получается при учете большего числа членов ряда. Советскими учеными М. П. Вукаловичем и И. И. Новиковым в 1939 году было получено уравнение для реальных газов. Это уравнение можно применять к любому реальному газу, и в частности к перегретому водяному пару. Но в связи с тем, что практически это сложное уравнение использовать трудно, с его помощью были вычислены основные физические величины перегретого водяного пара при различных р и Т, составлены таблицы и построена диаграмма в i-s-координатах (или h-s-координатах), на основании которых и проводятся расчеты процессов изменения состояния водяного пара.
Рис. 3.1. Структура h-s-диаграммы (i-s-диаграммы)
H-s-диаграммы (или i-s-диаграммы, что то же самое) чаще всего содержат в себе данные о свойствах воды в жидком и газообразном состояниях, так как они представляют наибольший интерес с точки зрения теплотехники. Степень сухости - это параметр, показывающий массовую долю насыщенного пара в смеси воды и водяного пара. Значение x = 0 соответствует воде в момент кипения (насыщения). Значение х = 1, показывает, что в смеси присутствует только пар. При нанесении соответствующих точек в координатах (h, s), взятых из таблиц насыщения справочников свойств воды и водяного пара, при их соединении получаются кривые, соответствующие определенным степеням сухости. В таком случае, линия х = 0 является нижней пограничной кривой, а х = 1 - верхней пограничной кривой. Область, заключённая между этими кривыми, является областью влажного пара. Область ниже кривой х = 0, которая стягивается практически в прямую линию (не показана), соответствует воде. Область выше кривой х = 1 - соответствует состоянию перегретого пара. Критическая точка (К). При определенном, достаточно высоком давлении, называемом критическим, свойства воды и пара становятся идентичными. То есть исчезают физические различия между жидким и газообразным состояниями вещества. Такое состояние называют критическим состоянием вещества, которому соответствует положение критической точки. Следует заметить, что она на пограничной кривой лежит гораздо левее максимума этой кривой. Изотерма - изолиния, построенная методом объединения точек по значениям энтальпии и энтропии, соответствующих определенной температуре. Изотермы пересекают пограничные кривые с изломом и, по мере удаления от верхней пограничной кривой, асимптотически приближаются к горизонтали. На схеме для упрощения представлены только три изотермы: t + Δt; t; t - Δt. Изобара - изолиния, построенная методом объединения точек по значениям энтальпии и энтропии, соответствующих определенному давлению. Изобары не имеют изломов при пересечении пограничных кривых. На схеме представлены только три изобары: p + Δp; p; p - Δp. Изохора - изолиния, построенная методом объединения точек по значениям энтальпии и энтропии, соответствующих определенному объему. Изохоры на h-s-диаграмме в области перегретого пара, всегда проходит круче, чем изобары, и это облегчает их распознавание на одноцветных диаграммах. Построение изохор требует более кропотливой работы с таблицей состояний. На схеме представлены только три изохоры: v - Δv; v; v + Δv. Изотермы и изобары в области влажного пара совпадают по причине линейной зависимости в состоянии насыщения. С появлением доступных компьютеров и приложений большое распространение получили h-s-диаграммы в электронном виде. Такие диаграммы представляют собой обычный оконный интерфейс с полями для ввода исходных данных, графическими функциональными клавишами, и полем ответов. После ввода имеющихся данных, нажатием графической клавиши «Расчёт» или «Ввод» на клавиатуре компьютера можно вызвать нужную информацию при условии соблюдения введённых параметров. Например, h-s-диаграмма воды и водяного пара «enekcalc3» - это компьютерная программа, которая позволяет находить такие параметры воды и водяного пара, как, давление, температура, энтальпия, энтропия и другие, когда известны один или два любых параметра. Параметры определяются как на линии насыщения, так и в области сухого и влажного пара. Пример получаемых при этом результатов показан в таблице на рис. 3.2. Есть и другие программы. Пример h-s-диаграммы воды и водяного пара показан на рис. 3.3.
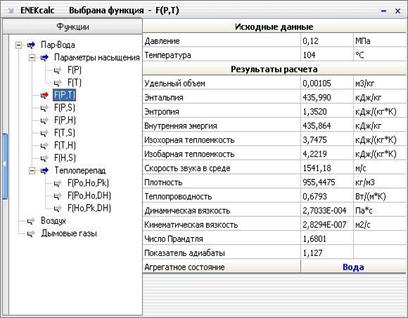
Рис. 3.2. Пример результатов расчета h-s-диаграммы воды и водяного пара по программе «enekcalc3», сайт ее разработчика: www.tef.kgtu.runnet.ru
Пары бывают насыщенные и перегретые. Насыщенные пары делят на сухие насыщенные (или просто сухие) и влажные насыщенные (или просто влажные). Испарением называется парообразование, происходящее только с поверхности жидкости и при любой температуре. Интенсивность испарения зависит от природы жидкости и ее температуры. Испарение жидкости может быть полным, если над жидкостью находится неограниченное пространство. В природе процесс испарения жидкости осуществляется в гигантских масштабах в любое время года. Пример этого - испарение воды в реках, морях и океанах. Явление испарения заключается в том, что отдельные молекулы жидкости, которые находятся у ее поверхности и обладают высокими скоростями, а следовательно, и большей по сравнению с другими молекулами кинетической энергией, вылетают из жидкости в окружающее пространство, преодолевая силовое действие соседних молекул, создающее поверхностное натяжение.
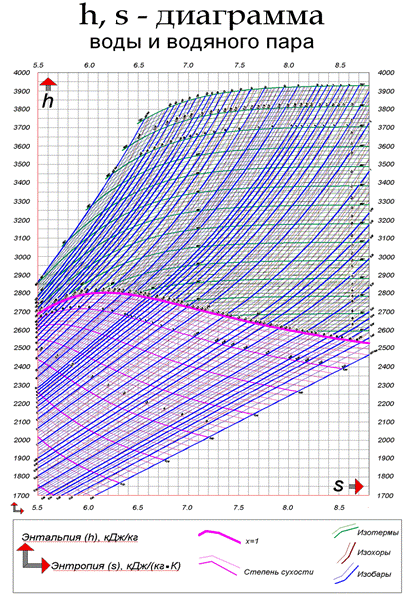
Рис. 3.3. Пример h-s-диаграммы воды и водяного пара С увеличением температуры интенсивность испарения возрастает, так как увеличиваются скорость и энергия молекул и уменьшаются силы их взаимодействия. При испарении температура жидкости снижается, так как из нее вылетают молекулы, обладающие сравнительно большими скоростями, вследствие чего уменьшается средняя скорость оставшихся в ней молекул. При сообщении жидкости теплоты повышаются ее температура и интенсивность испарения. При некоторой температуре, зависящей от природы жидкости и давления, под которым она находится, начинается парообразование во всей ее массе. При этом у стенок сосуда и внутри жидкости образуются пузырьки пара. Это явление называется кипением жидкости. Давление получающегося при этом пара такое же, как и среды, в которой происходит кипение. Процесс, обратный парообразованию, называется конденсацией. Этот процесс превращения пара в жидкость также происходит при постоянной температуре, если давление остается постоянным. Жидкость, образующаяся при конденсации пара, называется конденсатом. При испарении жидкости в ограниченное пространство (а это бывает в паровых котлах) одновременно происходит и обратное явление - конденсация пара, обусловленная тем, что некоторые из молекул пара, движущиеся в паровом пространстве по всем направлениям, ударяясь о поверхность жидкости, попадают в сферу влияния ее молекул и остаются в ней. Если скорость конденсации станет равной скорости испарения, то в системе наступает динамическое равновесие. Пар в этом состоянии имеет максимальную плотность и называется насыщенным. То есть насыщенным называют пар, находящийся в равновесном состоянии с жидкостью, из которой он образуется. Основное свойство этого пара состоит в том, что он имеет температуру, являющуюся функцией его давления, одинакового с давлением той среды, в которой происходит кипение. Если объем пара уменьшается, то часть пара переходит в жидкость (конденсация больше испарения). Но в обоих случаях давление пара р остается постоянным. Пар образуется до тех пор, пока не испарится последняя капля жидкости. Этому моменту будет соответствовать состояние сухого насыщенного пара. Пар, получаемый при неполном испарении жидкости, называют влажным насыщенным паром. Он является смесью сухого пара с капельками жидкости, распределенными в нем равномерно во взвешенном состоянии. Массовая доля сухого пара во влажном паре называется степенью сухости или массовым паросодержанием и обозначается через х. Массовая доля жидкости во влажном паре называется степенью влажности и обозначается через у. у = 1 - х. Степень сухости и степень влажности выражают или в долях единицы, или в %. Например, если х = 0,95 и у = 1- х = 0,05, то это означает, что в смеси находится 95% сухого пара и 5% кипящей жидкости. Если температура пара выше температуры насыщенного пара того же давления, то такой пар называется перегретым. Разность между температурой перегретого пара и температурой насыщенного пара того же давления называется степенью перегрева.
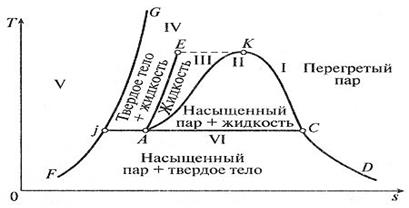
Рис. 3.4. Фазовая диаграмма для водяного пара в T-s координатах. Область I – газообразное состояние (перегретый пар, обладающий свойствами реального газа). Область II – равновесное состояние воды и насыщенного водяного пара (двухфазное состояние). Область II также называют областью парообразования. Область III – жидкое состояние (вода). Область III ограничена изотермой ЕК. Область IV – равновесное состояние твердой и жидкой фаз. Область V – твердое состояние. Области III, II и I разделены пограничными линиями AK (левая линия) и KD (правая линия). Общая точка K для пограничных линий AK и KD обладает особыми свойствами и называется критической точкой. Эта точка имеет параметры pкр, vкр и Ткр, при которых кипящая вода переходит в перегретый пар, минуя двухфазную область. Следовательно, вода не может существовать при температурах выше Ткр. Критическая точка К имеет следующие параметры: pкр = 22,136 МПа; vкр = 0,00326 м3/кг; tкр = 374,15 °С. Значения p, t, v и s для обеих пограничных линий приводятся в специальных таблицах термодинамических свойств водяного пара. На рисунках 3.5 и 3.6 изображены процессы нагрева воды до кипения, парообразования и перегрева пара в p-v - и T-s -диаграммах [1]. Начальное состояние жидкой воды, находящейся под давлением p 0 и имеющей температуру 0 °С, изображается на диаграммах p-v и T-s точкой а. При подводе теплоты при p = const температура ее увеличивается и растет удельный объем. В некоторый момент температура воды достигает температуры кипения. При этом ее состояние обозначается точкой b. При дальнейшем подводе теплоты начинается парообразование с сильным увеличением объема. При этом образуется двухфазная среда - смесь воды и пара, называемая влажным насыщенным паром. Температура смеси не меняется, так как тепло расходуется на испарение жидкой фазы. Процесс парообразования на этой стадии является изобарно-изотермическим и обозначается на диаграмме как участок bc. Затем в некоторый момент времени вся вода превращается в пар, называемый сухим насыщенным паром. Это состояние обозначается на диаграмме точкой c.
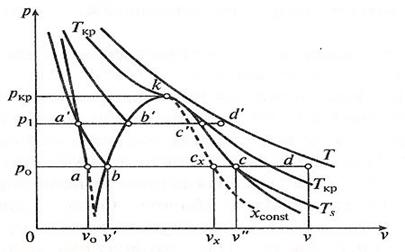
Рис. 3.5. Диаграмма p-v для воды и водяного пара.
При дальнейшем подводе теплоты температура пара будет увеличиваться и будет протекать процесс перегрева пара c - d. Точкой d обозначается состояние перегретого пара. Расстояние точки d от точки с зависит от температуры перегретого пара.
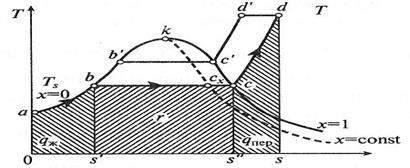
Рис. 3.6. Диаграмма T-s для воды и водяного пара.
Индексация для обозначения величин, относящихся к различным состояниям воды и пара: - величина с индексом «0» относится к начальному состоянию воды; - величина с индексом «′» относится к воде, нагретой до температуры кипения (насыщения); - величина с индексом «″» относится к сухому насыщенному пару; - величина с индексом «x» относится к влажному насыщенному пару; - величина без индекса относится к перегретому пару. Процесс парообразования при более высоком давлении p1 > p0 можно отметить, что точка a, изображающая начальное состояние воды при температуре 0 °С и новом давлении, остается практически на той же вертикали, так как удельный объем воды почти не зависит от давления. Точка b′ (состояние воды при температуре насыщения) смещается вправо на p-v -диаграмме и поднимается вверх на T-s -диаграмме. Это потому, что с увеличением давления увеличивается температура насыщения и, следовательно, удельный объем воды. Точка c′ (состояние сухого насыщенного пара) смещается влево, т. к. с увеличением давления удельный объем пара уменьшается, несмотря на увеличение температуры. Соединение множества точек b и c при различных давлениях дает нижнюю и верхнюю пограничные кривые ak и kc. Из p - v -диаграммы видно, что по мере увеличения давления разность удельных объемов v″ и v′ уменьшается и при некотором давлении становится равной нулю. В этой точке, называемой критической, сходятся пограничные кривые ak и kc. Состояние, соответствующее точке k, называется критическим. Оно характеризуется тем, что при нем пар и вода имеют одинаковые удельные объемы и не отличаются по свойствам друг от друга. Область, лежащая в криволинейном треугольнике bkc (в p-v -диаграмме), соответствует влажному насыщенному пару. Состояние перегретого пара изображается точками, лежащими над верхней пограничной кривой kc. На T-s -диаграмме площадь 0 abs′ соответствует количеству теплоты, необходимого для нагрева жидкой воды до температуры насыщения. Количество подведенной теплоты, Дж/кг, равное теплоте парообразования r, выражается площадью s′bcs, и для нее имеет место соотношение: r = T (s″ - s′). Количество подведенной теплоты в процессе перегрева водяного пара изображается площадью s″cds. На T-s -диаграмме видно, что по мере увеличения давления теплота парообразования уменьшается и в критической точке становиться равной нулю. Обычно T-s -диаграмма используется при теоретических исследованиях, так как практическое применение ее сильно затрудняет то, что количества теплоты выражаются площадями криволинейных фигур.
3. Термодинамический анализ теплотехнических устройств. Термодинамические циклы Для термодинамического анализа теплотехнических устройств используют термодинамические циклы для идеальных газов и критерии подобия. Второй закон термодинамики устанавливает, возможен или невозможен тот или иной процесс, в каком преимущественном направлении будет он протекать, когда система достигнет термодинамического равновесия, и при каких условиях от системы можно получить максимальную работу. Применительно к тепловым явлениям второй закон термодинамики устанавливает весьма важную специфическую особенность превращения теплоты в работу в тепловых двигателях. Чтобы выяснить эту особенность, а также условия, при которых осуществляется процесс преобразования теплоты в работу, и понять сущность второго закона термодинамики, рассмотрим, как должно изменяться состояние рабочего тела в такой непрерывно действующей машине, как поршневой тепловой двигатель. Для того чтобы цикл был обратимым, в нем должна быть исключена передача теплоты при наличии разности температур, иначе нарушается условие адиабатичности процесса. Поэтому передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, например, его частный случай цикл Брайтона). Для того чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведен к циклу Карно. Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД. Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведенной в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.
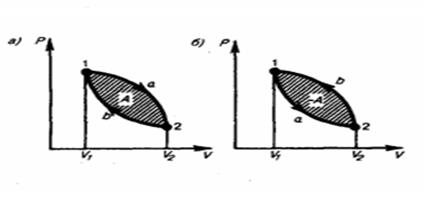
Рис. 3.7. Произвольный прямой (а) и обратный (б) циклы в p-v-диаграмме, А – работа цикла Полученная в цикле работа А может быть использована для вращения машин и механизмов и называется полезной. Самым характерным в работе непрерывно действующего поршневого теплового двигателя является возвращение поршня в первоначальное положение, а рабочего тела - в исходное состояние. В другого рода непрерывно действующих двигателях возвращение поршня в первоначальное положение может быть заменено каким-либо другим условием, но возвращение рабочего тела в исходное состояние обязательно. Это обстоятельство обусловливает то, что все тепловые двигатели работают по круговым процессам, или циклам. Прямой термодинамический цикл теплосиловой установки – это термодинамический цикл, в котором часть теплоты, сообщаемой рабочему телу, преобразуется в полезную работу. По прямым циклам работают все тепловые двигатели. Полезная работа цикла в p-v-диаграмме изображается площадью А, заключенной внутри кругового процесса. При этом цикл называется обратимым, если он состоит лишь из обратимых процессов, в противном случае цикл называется необратимым. Цикл называется прямым, если линии процессов расширения в p-v-диаграмме расположены выше линий процессов сжатия (рис. 3.7, а), т. е. в этих циклах производится работа, отдаваемая внешнему потребителю. Цикл называется обратным, если в p-v-диаграмме линии процессов сжатия расположены выше линий процессов расширения (рис. 3.7, б). Обратный термодинамический цикл теплосиловой установки – это термодинамический цикл, в котором за счет затраты работы осуществляется передача теплоты от менее нагретого тела к более нагретому. В этом случае работа А, ограниченная контуром цикла, осуществляется от постороннего источника энергии. Если рабочее тело в прямом цикле в процессе расширения получило от горячего (высшего) источника теплоту q1, а в процессе сжатия отдало холодному (низшему) источнику количество теплоты q2, то разность q1 – q2 = qц как теплота исчезает в течение цикла в результате преобразования ее в механическую энергию, т. е. в соответствии с первым законом термодинамики qц = Ац. Поэтому qц называется полезной теплотой. Поскольку в круговом процессе рабочее тело возвращается в первоначальное состояние, то ∆Uц = 0. В обратном цикле направление величин q1 и q2 изменяется на обратное, т. е. теплота q2 передается рабочему телу от холодного источника, а теплота q1 отдается горячему источнику. Следовательно, в обратном цикле теплота переходит от холодного тела к горячему, но это, как уже было сказано, должно обязательно сопровождаться затратой работы. Обратные циклы осуществляются в холодильных установках. Итак, непрерывно действующая тепловая машина должна работать по определенному циклу и иметь по крайней мере два источника теплоты: один – «горячий» с температурой T1, а другой – «холодный» с температурой Т2 (Т1 > Т2), и поэтому в ней невозможно целиком перевести в работу всю теплоту q1, подведенную к рабочему телу. Часть этой теплоты в виде q2 неминуемо должна быть отдана холодному источнику, и только разность между этими количествами теплоты превращается в механическую энергию. Это утверждение, высказанное впервые в 1824 году французским инженером и ученым Сади Карно, и составляет сущность второго закона термодинамики. «Повсюду, - писал Карно, - где имеется разность температуры, может происходить возникновение движущей силы. Движущая сила тепла не зависит от агентов, взятых для ее развития: ее количество исключительно определяется температурой тел, между которыми в конечном счете производится перенос тепла. Температура газа должна быть первоначально как можно выше, чтобы получить значительное развитие движущей силы. По той же причине охлаждение должно быть как можно больше. Нельзя надеяться хотя бы когда-либо практически использовать всю движущую силу топлива». Эти положения Карно служат фактически формулировками второго закона термодинамики, так как они устанавливают условия, при которых (в тепловых двигателях) возможно превращение теплоты в работу, и показывают, от чего собственно зависит эффективность этого превращения. Из изложенного следует, что в тепловых двигателях процессу преобразования теплоты в работу (основной процесс) должен обязательно сопутствовать процесс передачи теплоты холодному источнику (дополнительный процесс). При превращении механической энергии в тепловую (например, при трении) основной процесс может протекать без дополнительного сопровождающего. Такие процессы, которые протекают самостоятельно или, как говорят, «сами по себе», называют самопроизвольными. В природе существует большое количество таких процессов, которые в одном направлении протекают легко - «сами по себе», не требуя никаких дополнительных процессов (например, переход теплоты от горячего тела к холодному), а в обратном направлении не могут осуществляться самостоятельно (например, переход теплоты от холодного тела к горячему в холодильных установках возможен только при дополнительном процессе совершения механической работы). Поэтому немецкий физик Р. Клаузиус в 1850 году сформулировал второй закон термодинамики так: «Теплота не может переходить сама по себе от одного тела к другому, имеющему температуру более высокую, чем первое тело». Широкое изучение самопроизвольных процессов - диффузии, перехода теплоты от тела, более нагретого, к телу, менее нагретому, при конечной разности температур, процессов растворения и других - показывает, что все они являются необратимыми. Это позволило в наиболее общем виде второй закон термодинамики сформулировать так: любой реальный самопроизвольный процесс является необратимым. Все рабочие формулировки второго закона являются частными случаями этой наиболее общей формулировки. Например: а) невозможно с помощью неодушевленного материального агента получить от какой-либо массы вещества механическую работу путем охлаждения ее ниже температуры самого холодного из окружающих предметов (В. Томсон); б) невозможно построить периодически действующую машину, все действие которой сводилось бы к поднятию некоторого груза и охлаждению теплового источника (М. Планк); в) невозможно осуществить перпетуум мобиле (вечный двигатель) второго рода (В. Оствальд). Для оценки работы непрерывно действующей машины важно знать долю теплоты от q 1, превращенную в полезную энергию. В идеальных тепловых машинах, в которых нет потерь на трение, излучения, утечки рабочего тела через неплотности и других потерь, степень совершенства цикла принято оценивать термическим коэффициентом полезного действия (КПД), обозначаемым ή t и равным отношению Чем больше %, тем более совершенной будет тепловая установка, ибо в ней из всей сообщенной рабочему телу теплоты от горячего источника превращается в механическую энергию максимально возможная доля теплоты от q 1. Этого можно достичь лишь путем наиболее целесообразного подбора тех процессов, из которых образуется цикл. Из определения термического КПД следует, что понятие об этой величине тесно увязывается с сущностью второго закона термодинамики. Вопрос о максимальной доле теплоты, которая может быть при заданных условиях превращена в механическую энергию, был решен Сади Карно, который в 1824 году предложил цикл, получивший название цикла Карно. Цикл Карно Цикл Карно состоит из преобразования теплоты в работу при наличии только двух источников теплоты: верхнего с температурой Т1 и нижнего с температурой Т2 < Т1. В прямом цикле Карно тело от точки 1 расширяется сначала при Т1 = const с подводом теплоты q1 на участке 1 – а, затем в адиабатном процессе до точки 2, охлаждаясь до температуры Т2 = c onst, после этого сжимается при Т2 = const с отводом теплоты q2 на участке 2 – b, а потом по адиабате до восстановления первоначальных параметров в точке 1. На рис. 3.8 в p - v - и T - s -диаграммах представлен цикл Карно.
Рис. 3.8. Цикл Карно Рабочее тело (1 кг газа) находится в цилиндре под поршнем. Стенки полностью теплоизолируют цилиндр, что обеспечивает возможность осуществления адиабатного процесса изменения состояния газа. Однако в случае необходимости газ может приходить в соприкосновение с двумя источниками теплоты, имеющими температуру Т1 и Т2. Начальное состояние газа в p - v - и T - s -диаграммах характеризуется точкой 1, соответствующей крайнему верхнему положению поршня в цилиндре (ВМТ). От этой точки Карно предложил осуществлять изотермический процесс расширения 1-2, но так как этот процесс может протекать лишь при подводе теплоты к газу, то на участке 1-2 рабочее тело приходит в соприкосновение с горячим источником, имеющим температуру Т1, и получает от него количество теплоты q 1. Естественно, что для обратимого процесса и температура газа в этом процессе будет также Т1. В T-s-диаграмме этот процесс изобразится прямой, параллельной оси абсцисс, причем точка 2 будет правее точки 1 и площадь 1-2-5-6 графически будет измерять количество подведенной теплоты q 1. От точки 2 Карно предложил продолжать процесс расширения до нижней мертвой точки (НМТ) по адиабате 2-3; полная работа расширения в р- v -диаграмме измеряется площадью под линией 1-2-3. В Т- s -диаграмме адиабата расширения от точки 2 пойдет вниз, так как температура рабочего тела снижается из-за уменьшения внутренней энергии, затрачиваемой на работу расширения газа. Точка 3 характеризует конечное состояние рабочего тела, и для возврата его в начальное состояние (точка 1) Карно предложил осуществлять процесс сжатия по изотерме 3-4. Но так как этот процесс может протекать лишь при отводе теплоты от газа, то на участке 3-4 рабочее тело приходит в соприкосновение с холодным источником, имеющим температуру Т2, и отдает ему количество теплоты q 2. Температура газа в этом обратимом процессе будет также Т2. В T-s-диаграмме этот процесс изобразится изотермой Т2, пересечение которой с адиабатой, выходящей из точки 2, и даст точку 3. Конец изотермического процесса сжатия (точка 4) выбирают так, чтобы газ, продолжая сжиматься, вернулся в свое исходное состояние (точка 1), но уже по адиабате. Таким образом, процесс 4-1 – это адиабата сжатия. Суммарная работа, затрачиваемая на сжатие газа в p-v-диаграмме, графически изобразится площадью под кривой процесса 3-4-1. В Т-s-диаграмме положение точки 4 определится пересечением изотермы Т2 и адиабаты, проходящей через точку 1. Количество теплоты q2, отдаваемой холодному источнику, графически будет измеряться площадью прямоугольника 3-4-6-5. Выбор для цикла Карно двух изотерм и двух адиабат вполне обоснован, так как процессы подвода и отвода теплоты в цикле могут осуществляться только по изотермам, так как изотермический процесс - это единственный обратимый процесс, который может находиться под воздействием одного источника теплоты. Переход с одной изотермы 1-2 на другую 3-4 в цикле должен быть без теплообмена с внешней средой, поэтому кроме изотерм в цикле должны быть две обратимые адиабаты, одна из которых соответствует процессу расширения 2-3, а другая - процессу сжатия 4-1. Очевидно, работа в цикле Карно А v в p - v -диаграмме измеряется площадью 1-2-3-4, ограниченной двумя изотермами 1-2 и 3-4 и двумя адиабатами 2-3 и 4-1, а полезная теплота qv в T - s -диаграмме измеряется площадью прямоугольника 1-2-3-4. Термический КПД для рассмотренного обратимого цикла Карно может быть выражен так: или Из формулы (3.3) следует: 1) термический КПД зависит исключительно от температуры источника и от температуры холодильника; 2) термический КПД цикла Карно увеличивается при возрастании температуры источника Тх и при уменьшении температуры холодильника Т2; 3) термический КПД цикла Карно всегда меньше единицы и не может быть равен ей, так как это могло бы быть лишь при Т2/Т1 = 0, т. е. при Т1 = ∞ или Т2 = 0, но как первое, так и второе условие неосуществимы. В тепловых двигателях температура холодильника - это обычно температура окружающей среды Т2 = 260-300 К; температура горячего источника для паросиловых установок составляет около 2000 К (температура в топке), в поршневых двигателях внутреннего сгорания, где стенки цилиндра охлаждаются и сами продукты сгорания являются рабочим телом, Т1 ≈ 2500 К. Таким образом, теплоту, получаемую в цикле газом, невозможно полностью обратить в работу, и превращение теплоты в работу при всех условиях сопровождается переходом некоторого количества теплоты от источника к холодильнику. 4) термический КПД цикла Карно при Т1 = Т2 равен нулю, что указывает на невозможность превращения теплоты в работу, если все тела системы имеют одинаковую температуру, т. е. находятся в тепловом равновесии.
|
||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.84.179 (0.019 с.) |

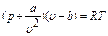 (3.1)
(3.1)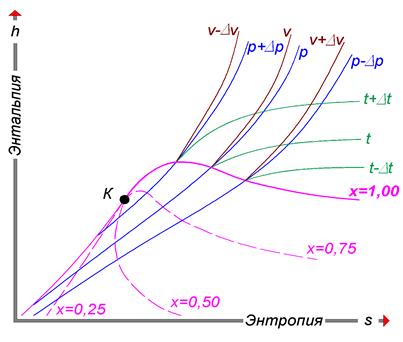
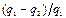 , т.е.
, т.е. 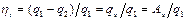 . (3.2)
. (3.2) 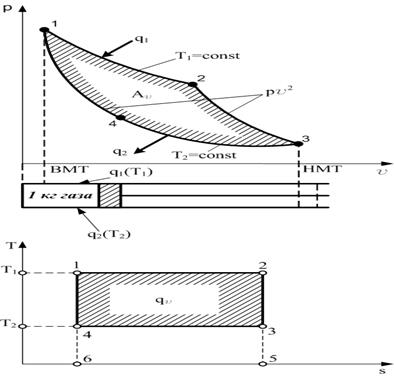
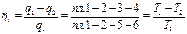

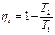 (3.3)
(3.3)


