Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия однозначности, начальные и граничные условияСодержание книги
Поиск на нашем сайте
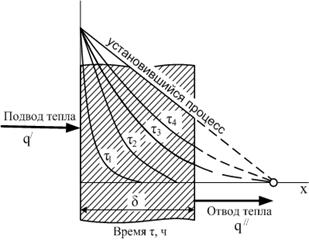
Дифференциальное уравнение теплопроводности описывает явление в самом общем виде, т. е. описывает класс явлений теплопроводности. Чтобы рассмотреть любой конкретный процесс, следует дать дополнительное математическое описание этого конкретного процесса теплопроводности, называемое условиями однозначности (единственности), которые включают в себя: 1 - геометрическую форму и размеры тела, в котором протекает процесс: 2 - граничные условия, характеризующие физическую связь тела с окружающей средой; 3 - начальные условия распределения температур в начальный момент времени и условия протекания процесса во времени; 4 - физические свойства тела и окружающей среды, определяемые физическими параметрами; 5 - интенсивность и распределение внутренних источников теплоты. Совокупность начальных и граничных условий называют краевыми условиями. Начальные условия при нагреве (или охлаждении) тела сказываются только в начальный период, но по истечении некоторого времени наступает регулярный режим, при котором распределение температур в теле определяется только граничными условиями и не зависит от начальных условий. Граничные условия задаются соответственно способу нагрева (охлаждения), т. е. воздействию окружающей среды на тело. 1. Если задается изменение температуры на поверхности тела во времени tпов = f (τ), то это отвечает граничным условиям первого рода. На практике встречаются случаи нагрева или охлаждения при заданном изменении температуры на поверхности, например по прямолинейному закону t пов = t 0 + bτ. При очень интенсивном теплообмене температура стенки близка к температуре среды, т.е. tокр = tпов, и этот случай близок к условиям первого рода. 2. Если на поверхности тела задана плотность теплового потока, то мы имеем граничные условия второго рода. По закону Фурье Градиент температуры относится к точке тела, расположенной в непосредственной близости от поверхности тела (х = + 0). 3. Граничные условия третьего рода соответствуют случаю конвективного теплообмена с поверхностью тела (конвективной теплоотдаче). Тепловой баланс на границе тела имеет вид: Этот случай часто применяют при решении практических задач. Различают два режима распространения тепла в теле: а) при установившемся (стационарном) режиме, когда температурное поле тела не изменяется во времени, т. е. когда температура каждой точки постоянна (dt /дх = 0 ); б) при неустановившемся (нестационарном) режиме, когда происходит нагрев или охлаждение тела, т, е. когда температурное поле изменяется с течением времени. На рис. 4.5 показан процесс одностороннего прогрева плоской стенки (пластины). Сначала нагревается внутренняя поверхность стенки. Постепенно теплота распространяется все глубже в толщу материала, и, наконец, после более или менее продолжительного времени наступает установившийся процесс распространения теплоты. Это происходит, когда стенка вполне прогрелась и теплота больше не расходуется на увеличение энтальпии ее материала, а температура ее остается неизменной.
Рис. 4.5. Процессы прогрева плоской стенки: кривые показывают распределение температур через время τ1, τ2, τ3 и т.д. от начала нагрева. На практике процессы нагревания и охлаждения в условиях нестационарных режимов встречаются очень часто. Так, в промышленных печах изделия подвергаются нагреву для тепловой обработки материала. В регенеративных теплообменниках греющей средой сначала нагревается теплоемкая насадка, а затем эта насадка отдает теплоту нагреваемой среде. Принцип регенерации используется и в отопительных комнатных печах: в то время когда они топятся, разогревается кладка, а после закрытия трубы тепло нагретой кладки постепенно распространяется по помещению, где установлена печь.
|
||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.255.122 (0.005 с.) |

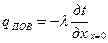 (4.15)
(4.15)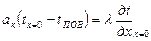
 ( 4.16 )
( 4.16 )