
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Температуры и тепловой потокСодержание книги
Поиск на нашем сайте
Картина распределения температур в пространстве, занятом телом, характеризуется температурным полем, представляющим собой совокупность значений температур t в этот момент времени t для всех точек пространства. Если температура является функцией одних только пространственных координат (х, у, z), то такое поле называется стационарным или установившимся. Но часто температура каждой точки тела зависит также и от времени t, т.е. t является функцией от (х, у, z, t), и тогда поле называется нестационарным или неустановившимся. Геометрическое место точек, имеющих одинаковую температуру, называют изотермической поверхностью. Так как в одной точке не может быть двух разных температур, то изотермические поверхности не могут пересекаться и они замыкаются на себя, располагаясь внутри тела или на его границах.
Если взять две близко расположенные друг к другу изотермические поверхности (рис. 4.2) с температурами t и t + ∆ t, то, перемещая точку О в направлении х, пересекающем изотермы, будем наблюдать изменение температуры. Наибольшее изменение температуры на единицу длины будет в направлении нормали n к изотермическим поверхностям. Предел отношения изменения температуры ∆ t к расстоянию между изотермами по нормали n называют температурным градиентом: Температурный градиент является вектором, направленным по нормали к изотермической поверхности, причем за положительное направление вектора принимается направление в сторону возрастания температур, т. е. dt / dn > 0. Если же вектор направлен в сторону убывающей температуры, то производная dt / dn будет отрицательной. Температурный градиент показывает, насколько интенсивно (резко) меняется температура в толще тела и является важной величиной, определяющей многие физические явления (появление трещин в хрупком теле от неравномерного нагрева, термические деформации и т. д.). Количество тепла Q, проходящее в единицу времени через изотермическую поверхность F, называют тепловым потоком. Тепловой поток q на 1 м2 поверхности называют удельным тепловым потоком, плотностью теплового потока или тепло вой нагрузкой поверхности нагрева. q = Q / F, Вт/м2. (4.5) Величины Q и q являются векторами, направленными по нормали к изотермической поверхности, причем за положительное направление принимается направление в сторону уменьшения температуры. Векторы теплового потока и градиента температур противоположны. Линии, касательные к которым совпадают с направлением вектора теплового потока, называют линиями теплового потока. Эти линии перпендикулярны к изотермическим поверхностям (рис. 4.3). Основной закон теплопроводности (закон Фурье) формулируется так: плотность теплового потока пропорциональна градиенту температуры: где λ - коэффициент теплопроводности, являющийся в формуле (4.6) коэффициентом пропорциональности. Коэффициент теплопроводности λ, Вт/(м∙К), численно равен количеству теплоты, передаваемой в единицу времени через 1 м поверхности стенки толщиной 1 м при разности температур в 1 градус. Общее количество теплоты, переданное теплопроводностью через стенку поверхностью F м2 за время t, составит Q = qFt, Дж. (4.7) Величина коэффициента теплопроводности λ зависит от природы тел и от их температуры. Для большинства материалов эта зависимость является линейной: λ t = λo (1 + bt), (4.8) где λ o и λ t - значения коэффициентов теплопроводности соответственно при 0°С и при t °C; b - постоянная, определяемая экспериментально. Самые плохие проводники теплоты - газы (для них λ = 0,006-0,6 Вт/(м·град). Некоторые чистые металлы, наоборот, имеют высокие значения λ и для них величина его колеблется от 12 до 420 Вт/(м·град). Примеси к металлам вызывают значительное уменьшение коэффициента теплопроводности. Например, у чугуна λ тем меньше, чем больше содержится в чугуне углерода. Для строительных материалов λ = 0,16-1,4 Вт/(м·град). Пористые материалы, плохо проводящие теплоту, называют теплоизоляционными и для них значения λ находятся в пределах от 0,02 до 0,23 Вт/(м·град). Чем больше пористость материала, т. е. чем больше содержится в нем пузырьков малотеплопроводного воздуха, тем меньше он теплопроводен.
|
||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.42.247 (0.005 с.) |



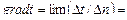 dt / dn, град/м. (4.4)
dt / dn, град/м. (4.4)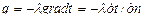 , (4.6)
, (4.6)


