Алгоритм формирования дерева решений по обучающей выборке

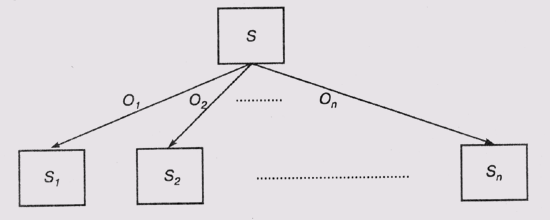
Ниже будет описан алгоритм формирования дерева решений по обучающей выборке, использованный в системе IDЗ. Задача, которую решает алгоритм, формулируется следующим образом. Задано:

множество целевых непересекающихся классов {С1, С2,..., Сk};

Обучающая выборка S, в которой содержатся объекты более чем одного класса.

Алгоритм использует последовательность тестовых процедур, с помощью которых множество 5 разделяется на подмножества, содержащие объекты только одного класса. Ключевой в алгоритме является процедура построения дерева решений, в котором нетерминальные узлы соответствуют тестовым процедурам, каждая из которых имеет дело с единственным атрибутом объектов из обучающей выборки. Как вы увидите ниже, весь фокус состоит в в выборе этих тестов.

Пусть Т представляет любую тестовую процедуру, имеющую дело с одним из атрибутов, а {О1,O2,...,On}— множество допустимых выходных значений такой процедуры

при ее применении к произвольному объекту х. Применение процедуры Т к объекту х будем обозначать как Т(х). Следовательно, процедура Т(х) разбивает множество S на составляющие { S₁, S₂,..., S_n}, такие, что

S_i= {x|T(x) = O_i}. Такое разделение графически представлено на рис. 20.3.

Рис. 20.3. Дерево разделения объектов обучающей выборки

Если рекурсивно заменять каждый узел S_i, на рис. 20.3 поддеревом, то в результате будет построено дерево решений для обучающей выборки S. Как уже отмечалось выше, ключевым фактором в решении этой проблемы является выбор тестовой процедуры — для каждого поддерева нужно найти наиболее подходящий атрибут, по которому можно выполнять дальнейшее разделение объектов.

Квинлан (Quinlan) использует для этого заимствованное из теории информации понятие неопределенности. Неопределенность — это число, описывающее множество сообщений M= { m₁, т₂,..., т_n}. Вероятность получения определенного сообщения m_i из этого множества определим как р(т_i). Объем информации, содержащейся в этом сообщении, будет в таком случае равен

I(m_i) = -logp(m_i).

Таким образом, объем информации в сообщении связан с вероятностью получения этого сообщения обратной монотонной зависимостью. Поскольку объем информации измеряется в битах, логарифм в этой формуле берется по основанию 2.

Неопределенность множества сообщений U(M) является взвешенной суммой количества информации в каждом отдельном сообщении, причем в качестве весовых коэффициентов используются вероятности получения соответствующих сообщений:

U(М) = -Sum_ip[ (m_i) logp(m_i), i = 1,..., п. ]

Интуитивно ясно, что чем большую неожиданность представляет получение определенного сообщения из числа возможных, тем более оно информативно. Если все сообщения в множестве равновероятны, энтропия множества сообщений достигает максимума.

Тот способ, который использует Квинлан, базируется на следующих предположениях.

Корректное дерево решения, сформированное по обучающей выборке S, будет разделять объекты в той же пропорции, в какой они представлены в этой обучающей выборке.

Для какого-либо объекта, который нужно классифицировать, тестирующую процедуру можно рассматривать как источник сообщений об этом объекте.

Пусть N_i — количество объектов в S, принадлежащих классу С_i. Тогда вероятность того, что произвольный объект с, "выдернутый" из S, принадлежит классу С_i, можно оценить по формуле

p(c~C_i) = N_i/|S|,

а количество информации, которое несет такое сообщение, равно I (с ~ С_i) = -1оg₂р(m_i) (с ~ С_i) бит.

Теперь рассмотрим энтропию множества целевых классов, считая их также множеством сообщений {С₁ C₂,..., C_k}. Энтропия также может быть вычислена как взвешенная сумма количества информации в отдельных сообщениях, причем весовые коэффициенты можно определить, опираясь на "представительство" классов в обучающей выборке:

U(M) = -Sum_i=1...,k[ р(с ~ C_i)x I(с ~ С_i)] бит.

Энтропия U(M) соответствует среднему количеству информации, которое необходимо для определения принадлежности произвольного объекта (с ~ S) какому-то классу до того, как выполнена хотя бы одна тестирующая процедура. После того как соответствующая тестирующая процедура Т выполнит разделение S на подмножества {S₁, S₂,..., S_n }, энтропия будет определяться соотношением

Uт(S) = -Sum_i=1,...k(|S|/|S_i|)х U(S_i).

Полученная оценка говорит нам, сколько информации еще необходимо после того, как выполнено разделение. Оценка формируется как сумма неопределенностей сформированных подмножеств, взвешенная в пропорции размеров этих подмножеств.

Из этих рассуждений очевидно следует эвристика выбора очередного атрибута для тестирования, используемая в алгоритме, — нужно выбрать тот атрибут, который сулит наибольший прирост информации. Прирост информации G_S(T) после выполнения процедуры тестирования Т по отношению к множеству 5 равен

G_S(7)=U(S)-Uт(S).

Такую эвристику иногда называют "минимизацией энтропии", поскольку увеличивая прирост информации на каждом последующем тестировании, алгоритм тем самым уменьшает энтропию или меру беспорядка в множестве.

Вернемся теперь к нашему примеру с погодой и посмотрим, как эти формулы интерпретируются в самом простом случае, когда множество целевых классов включает всего два элемента. Пусть р — это количество объектов класса П в множестве обучающей выборки S, а п — количество объектов класса Н в этом же множестве. Таким образом, произвольный объект принадлежит к классу П с вероятностью p / (p + п), а к классу Н с вероятностью n /(p + п). Ожидаемое количество информации в множестве сообщений М = {П, Н} равно

U(M) = -p / (p + п) log₂(p/(p + n)) -

n / (p + n) 1оg₂(n/(р + п))

Пусть тестирующая процедура Т, как и ранее, разделяет множество S на подмножества {S₁, S₂.....S_n }, и предположим, что каждый компонент S, содержит p_i, объектов класса

П и и, объектов класса Н. Тогда энтропия каждого подмножества S_i будет равна

U(S_i) = -р_i/(р_i + n_i) l og₂(p_i/(p_i + n_i)) -

n/(р_i + n_i) l og2(n_i/(p_i +n_i))

Ожидаемое количество информации в той части дерева, которая включает корневой узел, можно представить в виде взвешенной суммы:

U т(S) = -Sum_i=1,...n((p _i, + n_i)/ (р + n)) х U(S_i) Отношение (р, + п,)/(р + п) соответствует весу каждой i-и ветви дерева, вроде того, которое показано на рис. 20.3. Это отношение показывает, какая часть всех объектов S принадлежит подмножеству S,.

Ниже мы покажем, что в последней версии этого алгоритма, использованной в системе С4.5, Квинлан выбрал слегка отличающуюся эвристику. Использование меры прироста информации в том виде, в котором она определена чуть выше, приводит к тому, что предпочтение отдается тестирующим процедурам, имеющим наибольшее количество выходных значений {O₁ O₂,..., О _п } .

Но несмотря на эту "загвоздку", описанный алгоритм успешно применялся при обработке достаточно внушительных обучающих выборок (см., например, [Quintan, 1983]). Сложность алгоритма зависит в основном от сложности процедуры выбора очередного теста для дальнейшего разделения обучающей выборки на все более мелкие подмножества, а последняя линейно зависит от произведения количества объектов в обучающей выборке на количество атрибутов, использованное для их представления. Кроме того, система может работать с зашумленными и неполными данными, хотя этот вопрос в данной книге мы и не рассматривали (читателей, интересующихся этим вопросом, я отсылаю к работе [Quinlan, 1986, b]).

Простота и эффективность описанного алгоритма позволяет рассматривать его в качестве достойного соперника существующим процедурам извлечения знаний у экспертов в тех применениях, где возможно сформировать репрезентативную обучающую выборку. Но, в отличие от методики, использующей пространства версий, такой метод не может быть использован инкрементально, т.е. нельзя "дообучить" систему, представив ей новую обучающую выборку, без повторения обработки ранее просмотренных выборок.

Рассмотренный алгоритм также не гарантирует, что сформированное дерево решений будет самым простым из возможных, поскольку использованная оценочная функция, базирующаяся на выводах теории информации, является только эвристикой. Но многочисленные эксперименты, проведенные с этим алгоритмом, показали, что формируемые им деревья решений довольно просты и позволяют прекрасно справиться с классификацией объектов, ранее неизвестных системе. Продолжение поиска "наилучшего решения" приведет к усложнению алгоритма, а как уже отмечалось в главе 14, для многих сложных проблем вполне достаточно найти не лучшее, а удовлетворительное решение.

В состав программного комплекса С4.5, в котором используется описанный выше алгоритм, включен модуль C4.5Rules, формирующий из дерева решений набор порождающих правил. В этом модуле применяется эвристика отсечения, с помощью которой дерево решений упрощается. При этом, во-первых, формируемые правила становятся более понятными, а значит, упрощается сопровождение экспертной системы, а во-вторых, они меньше зависят от использованной обучающей выборки. Как уже упоминалось, в С4.5 также несколько модифицирован критерий отбора тестирующих процедур по сравнению с оригинальным алгоритмом, использованным в ID3.

Недостатком эвристики, основанной на приросте количества информации, является то, что она отдает предпочтение процедурам с наибольшим количеством выходных значений {О₁, O₂,..., О_n}. Возьмем, например, крайний случай, когда практически бесполезные тесты будут разделять исходную обучающую выборку на множество классов с единственным представителем в каждом. Это произойдет, если обучающую выборку с медицинскими данными пациентов классифицировать по именам пациентов. Для описанной эвристики именно такой вариант получит преимущество перед прочими, поскольку U_T(S) будет равно нулю и, следовательно, разность G_s(T) = U(S) - U_T(S) достигнет максимального значения.

Для заданной тестирующей процедуры Т на множестве данных S, которая характеризуется приростом количества информации G_S{T), мы теперь возьмем в качестве критерия отбора относительный прирост Н_S(Т), который определяется соотношением

Н_S{Т) = G_S(Т)/V(S),

Где

V(S) = -Sum_i=1,..., (|S|/|S_i|) x log2(|S|/|S_i|).

Важно разобраться, в чем состоит отличие величины V(S) от U(S). Величина V(S) определяется множеством сообщений {О₁, О₂,...,О_n] или, что то же самое, множеством подмножеств { S₁ S₂,...,S_n}, ассоциированных с выходными значениями тестовой процедуры, а не с множеством классов {С₁ C₂,...,C_k}. Таким образом, при вычислении величины V(S) принимается во внимание множество выходных значений теста, а не множество классов.

Новая эвристика состоит в том, что выбирается та тестирующая процедура, которая максимизирует определенную выше величину относительного прироста количества информации. Теперь те пустые тесты, о которых мы говорили чуть выше и которым прежний алгоритм отдал бы преимущество, окажутся в самом "хвосте", поскольку для них знаменатель будет равен log₂(N), где N — количество элементов в обучающей выборке.

Оригинальный алгоритм формирования дерева страдает еще одной "хворью" - он часто формирует сложное дерево, в котором фиксируются несущественные для задачи классификации отличия в элементах обучающей выборки. Один из способов справиться с этой проблемой — использовать правило "останова", которое прекращало бы процесс дальнейшего разделения ветвей дерева при выполнении определенного условия. Но оказалось, что сформулировать это условие не менее сложно, а потому Квинлан пошел по другому пути. Он решил "обрезать" дерево решений после того, как оно будет сформировано алгоритмом. Можно показать, что такое "обрезание" может привести к тому, что новое дерево будет обрабатывать обучающую выборку с ошибками, но с новыми данными оно обычно справляется лучше, чем полное дерево. Проблема "обрезания" довольно сложна и выходит за рамки данной книги. Читателям, которые заинтересуются ею, я рекомендую познакомиться с работами [Mingers, 1989, b] и [Mitchell, 1997], а подробное описание реализации этого процесса в С4.5 можно найти в [Quinlan, 1993, Chapter 4].

Для того чтобы сделать более понятным результат выполнения алгоритма, в системе С4.5 дерево решений преобразуется в набор порождающих правил. Мы уже ранее демонстрировали соответствие между отдельным путем на графе решений от корня к листу и порождающим правилом. Условия в правиле — это просто тестовые процедуры, выполняемые в промежуточных узлах дерева, а заключение правила — отнесение объекта к определенному классу.

Однако строить набор правил перечислением всех возможных путей на графе — процесс весьма неэффективный. Некоторые тесты могут служить просто для того, чтобы разделить дерево и таким образом сузить пространство выбора до подмножества, которое в дальнейшем уточняется с помощью проверки других, более информативных атрибутов. Это происходит по той причине, что не все атрибуты имеют отношение ко всем классам объектов.