
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ГЛАВА 2. Обзор алгоритмов обобщения с «учителем»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Алгоритм ДРЕВ
Алгоритм ДРЕВ [2] является методом качественного обобщения по признакам. Он был предложен как развитие алгоритма обобщения Э.Ханта CLS. Ставится цель построения обобщенного понятия на основе анализа обучающей выборки S, содержащей примеры На первом этапе работы алгоритма делается попытка сформировать обобщенное конъюнктивное понятие на основе поиска признаков, значения которых являются общими для всех объектов выборки Затем формируется обобщенное дизъюнктивное понятие В алгоритме ДРЕВ наиболее важное значение признака определяется с помощью одного из критериев существенности После разбиения выборок на подвыборки на основе найденного значения Описание алгоритма ДРЕВ
Приведем описание алгоритма ДРЕВ по шагам. 1) Формирование В случае успеха переход к п.2, иначе – к п.3. 2) Печать 3) Выбор признака 4) Разбиение выборок на две пары подвыборок. 5) Формирование В случае неудачи – возврат к шагу 3, иначе – переход к шагу 6. 6) Формирование и печать Алгоритм основан на разбиении выборок частных примеров на подвыборки в соответствии с наличием в них разделяющих значений признаков и позволяет получать логическую функцию принадлежности ценой небольшого числа просмотров этих выборок. К основным достоинствам алгоритма ДРЕВ можно отнести его компактность, быстроту сходимости, простой вид формируемых им понятий. Достоинством алгоритма также является то, что в алгоритме ДРЕВ на каждом шаге из дальнейшего рассмотрения удаляются признаки, имеющие для всех примеров и контрпримеров одинаковые значения и, следовательно, не несущие существенной информации. Это может быть особенно важно, если мы имеем дело с большим количеством признаков, и многие из них несущественны. 2.2. Алгоритм ID3(индукция решающих деревьев) Алгоритм ID3[4] строит такое решающее дерево, в котором каждому узлу сопоставлен атрибут, являющийся наиболее информативным среди всех атрибутов, еще не рассмотренных на пути от корня дерева. В качестве меры информативности обычно используется теоретико-информационное понятие энтропии. Пусть S – множество примеров обучающей выборки, и имеется n равновероятных значений атрибута. Вероятность p того, что значение атрибута, случайно взятого из S примера равно C, равна 1/ n и информация, сообщаемая нам значением атрибута равна –log p = log n (логарифм по основанию 2). В общем случае, если мы имеем дискретное распределение P = (p 1, p 2, …, pn), то передаваемая информация, или энтропия P, будет вычисляться как
Чем более равномерным является распределение, тем больше его энтропия. Если множество S примеров разбито на попарно непересекающиеся подмножества (классы) C1, C2, …, Ck, то информация, необходимая для того, чтобы идентифицировать класс примера, равна Info (S) = I (P), где P – дискретное распределение вероятностей, соответствующее набору классов C 1, C 2, …, Ck:
Разбив множество примеров на основе значений некоторого атрибута a на подмножества S 1, S 2, …, Sn, мы можем вычислить Info (S) как взвешенное среднее информации, необходимой для идентификации класса примера в каждом подмножестве:
Величина Gain (A, S) = Info(S) – Info (A, S) показывает количество информации, которое мы получаем благодаря атрибуту A (прирост информативности). Алгоритм ID3 использует эту величину для оценки информативности атрибута при построении решающих деревьев, что позволяет получать деревья минимальной высоты, то есть наиболее компактные и простые. Алгоритм ID3 не приспособлен для работы с числовыми атрибутами. Для того чтобы строить решающие деревья на основе обучающих выборок с признаками непрерывного типа, необходимо сначала их обработать и привести к дискретному типу, то есть даже если некоторый атрибут A имеет непрерывную область определения, в обучающем множестве имеется лишь конечное множество значений С1 < С2 < … < Сn. Для каждого значения Сi мы разбиваем примеры на те, у которых A £ Сi, и те, у которых A > Сi. Для каждого из возможных разбиений мы вычисляем Gain(A, S) и выбираем наиболее информативное разбиение. Итак, чтобы построить решающее правило посредством алгоритмом ID3, необходимо для начала выполнить дискретизацию числовых атрибутов, используя величину энтропии для поиска оптимального разбиения или воспользовавшись специальным алгоритмом дискретизации. Затем определить наиболее существенный (информативный) атрибут, разбиение множества примеров на подмножества, с помощью которого максимизирует прирост информативности. Самый «лучший» атрибут помещается в корень дерева, и формируются ветви для каждого из возможных значений этого атрибута. Если критерий окончания не выполняется необходимо повторить процедуру для каждого подмножества, иначе алгоритм заканчивает работу. Под критерием окончания подразумевается правило, которое должно определить, является ли рассматриваемый узел узлом-решением (листом), определяющим класс объекта, или внутренним узлом. В последнем случае узел помечается именем очередного «наилучшего» атрибута, и создаются ветви для каждого из возможных значений выбранного атрибута. В задаче построения деревьев решения может действовать несколько правил остановки, то есть момента, когда следует прекратить дальнейшее ветвление. Один из вариантов таких правил – ограничение глубины дерева, то есть максимально возможное количество вершин на пути от корня к листу. Еще один вариант – задание минимального количества примеров, которые будут содержаться в конечных узлах дерева. Следует отметить, что правило остановки позволяют уменьшить время на обучение модели, а также строить более компактные деревья, однако при их использовании точность классификации (успешность дерева решений) может значительно снизиться. Прекращение ветвления происходит в одном из следующих случаев: · все примеры на некотором листе принадлежат одному классу; · использованы все атрибуты. В этом случае лист помечается именем класса, который является наиболее популярным среди примеров подмножества. Для решения проблемы слишком ветвистого дерева используется восходящий метод объединения внутренних узлов операцией ИЛИ. Эта процедура не приводит к возрастанию ошибки решения задачи классификации, так как она лишь модифицирует вид дерева, не меняя концептуально решающее правило. Алгоритм ID3 хорошо зарекомендовал себя в широком спектре приложений. Деревья решений, построенные по этому алгоритму, являются гибким средством предсказания принадлежности объектов к определенному классу и обеспечивают высокое качество классификации. Использование статистики позволяет алгоритму работать с зашумленными и противоречивыми данными. После того, как алгоритм был впервые опубликован, ряд исследователей предложили различные его усовершенствования, улучшающие его работу, например, инкрементная версия алгоритма, которая позволяет не создавать дерево заново при добавлении одного примера, а перестроить его. Это свойство важно для того, чтобы учесть изменения в базах данных. Алгоритм AQ Описание алгоритма
Алгоритм AQ[5] формирует в качестве классификатора набор продукционных правил вида «ЕСЛИ <условие>, ТО <класс>» (одно правило для каждого класса). Условие в данном случае представляет собой конъюнкцию тестов для атрибутов. Пустое условие в правиле означает, что правило покрывает все примеры множества. Приведем пример правила для задачи «Игра в гольф»: ЕСЛИ (Wind=false) И (Outlook=sunny) ТО «Играть». В алгоритме AQ новый пример классифицируется следующим образом: среди всех сформированных решающих правил ищется то, которое покрывает пример. Если найдено только одно правило, то примеру присваивается значение класса, указанного в правиле. Если несколько правил покрывают пример, то значение класса выбирается как наиболее вероятное среди всех примеров обучающей выборки, которые покрываются найденными правилами. Если ни одно из сформированных правил не покрывает пример, то значение класса выбирается как наиболее часто встречающееся среди всех примеров обучающей выборки (значение класса по умолчанию). Ниже представлен псевдокод данного алгоритма. Алгоритм состоит из нескольких итераций, на каждой из которых формируется условие, покрывающее положительные примеры для текущего класса и не покрывающее ни одного отрицательного примера. Когда очередное правило найдено, все примеры, покрытые им, удаляются из обучающей выборки. Процедура повторяется снова до тех пор, пока в обучающей выборке остаются примеры текущего класса. Основные ограничения, которые могут быть заданы пользователем – это мощность множества STAR (starsize) и максимальная глубина формируемых продукционных правил (heapsize).
Псевдокод алгоритма Алгоритм AQ Исходные данные K – обучающая выборка A – множество предсказывающих признаков С – целевой (результирующий) атрибут (класс) Результат Набор продукционных правил Начало Для каждого значения Ci из значений класса C начало Выделить множество POS примеров класса Сi Выделить множество NEG примеров, отрицательных для класса Ci Положим множество тестов COVER (условие правила – дизъюнкция конъюнкций тестов для атрибутов) пусто. пока есть примеры в POS начало Произвольно выбрать пример SEED из POS //Выполнить поиск промежуточных условий STAR, которые покрывают пример SEED и не покрывают ни одного примера из NEG Положим STAR пусто Пока условия в STAR покрывают примеры из NEG начало Произвольно выбрать Eneg – пример из NEG //Исключить из STAR условия, покрывающие Eneg EXTENSION – тесты, покрывающие SEED, но не Eneg
Удалить все дублирующие условия в STAR конец Пока размер STAR > STARSIZE начало Удалить наихудшее условие конец Выбрать наилучшее условие BEST из STAR Добавить BEST в COVER Удалить из POS все примеры, покрываемые COVER конец Добавить продукционное правило: ЕСЛИ COVER, ТО Ci Конец Вывести набор продукционных правил Конец алгоритма
Для выбора наилучшего правила каждый раз вычисляется количество покрытых им примеров. На каждом этапе выбирается правило, для которого данное значение максимально. Предпочтение также отдается более простым, а значит более коротким правилам. Наилучшее условие, покрывающее пример SEED, выбирается исходя из суммы покрытых положительных и исключенных отрицательных примеров. При этом SEED (в переводе с англ. «зерно») выбирается случайным образом, и отрицательные примеры, находящиеся в непосредственной близости к примеру SEED, используются первыми для формирования STAR, что оказывает существенное влияние на формируемый набор решающих правил. В зависимости от того, какое «зерно» будет выбрано, вид продукционных правил будет различаться, а значит, успешность алгоритма, выражаемая в точности классификации новых примеров, также будет различной. Зависимость от случайно выбираемого примера является основным недостатком данного алгоритма. Так же есть несколько параметров, определяемых пользователем и влияющих на формируемые продукции – мощность множества STAR (starsize) и максимальная глубина правила (heapsize). Уменьшение параметра heapsize нежелательно, так как это влечет формирование достаточно общих и малонадежных правил. Размер множества STAR влияет на производительность алгоритма, поэтому этот параметр с одной стороны не должен быть большим, а с другой стороны должен позволять алгоритму работать более гибко и иметь возможность выбирать из условий наилучшее. При тестировании работы алгоритма CN2 использовались следующие значения параметров: starsize = 3, heapsize = 3. Итак, в результате работы алгоритма AQ формируется набор продукционных правил, а также правило по умолчанию (Default), которое применятся при классификации в тех случаях, когда для объекта не подходит ни одно решение из списка. Алгоритм CN2 Описание алгоритма
Данный алгоритм строит решающие правила для множества примеров обучающей выборки и является расширением алгоритма AQ, рассмотренного в разделе 2.3. Этот алгоритм просматривает все множество объектов и находит правило, которое является наилучшим среди всех возможных, добавляя его в конец набора формируемых продукционных правил. При этом в отличие от алгоритма AQ, алгоритм CN2 не исключает из рассмотрения правила, покрывающие один или несколько отрицательных примеров. После того, как наилучшее правило найдено, алгоритм удаляет из обучающей выборки покрываемые им примеры и повторяет процедуру поиска наилучшего правила для остальных объектов. Алгоритм заканчивает работу, когда невозможно выделить наилучшее правило для текущего набора объектов или примеры в обучающей выборке закончились. Главный недостаток алгоритма AQ – это невозможность работы в реальных базах данных, содержащих «зашумленные» данные. Это связано с тем, что алгоритм формирует продукционные правила, покрывающие примеры строго одного класса, поэтому любой ошибочный пример может повлиять на решение и на успешность классификации. Авторы алгоритма CN2 преследовали цель создать алгоритм, использующий подход AQ, но приспособленный для обработки данных, содержащих шум. Рассмотрим методику обобщения данных, используемую данным алгоритмом. Ниже представлен псевдокод алгоритма CN2. Псевдокод алгоритма Исходные данные K – обучающая выборка SELECTORS – все возможные проверки атрибутов С – целевой (результирующий) атрибут (класс) // Результат Набор продукционных правил RULELIST Начало Положим множество RULELIST пусто. Повторять Положим множество промежуточных условий STAR пусто. BestComplex – наилучшее условие Пока (STAR не пусто) или (длина BestComplex < HEAPSIZE) Начало //Создать условия STAR
Удалить все условия из NEWSTAR, дублирующие условия в STAR или противоречивые (big ˅ small) Для каждого условия Complex из NEWSTAR Начало Если Complex статистически важен и лучше чем BestComplex то BestComplex = Complex конец пока (размер NEWSTAR > STARSIZE) начало Удалить наихудшее условие из NEWSTAR Конец STAR = NEWSTAR конец Если (BestComplex!= nil) то K’ – примеры, покрытые условием BestComplex (несмотря на класс) Удалить из К примеры К’ C – значение класса, наиболее популярное среди примеров K’ Добавить к множеству RULELIST правило: ЕСЛИ BestComplex, то С До тех пор, пока (BestComplex!= nil) или (K пусто) Вывести RULELIST Конец алгоритма
В следующем разделе будет рассмотрен алгоритм ABCN, позволяющий учитывать условия/ограничения, заданные экспертом, которые влияют на конечный набор полученных продукционных правил и на результат классификации в частности. Алгоритм ABCN2
В данном разделе подробно описываются этапы получения продукционных правил с помощью алгоритма ABCN2 [6]. Рассматривается способ аргументирования примеров из выборки обучения, описывается способ оценки условий для формирования правил, поиск пороговых значений для атрибутов непрерывного типа, приводится пошаговое описание алгоритма.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 641; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.195 (0.013 с.) |

 и контрпримеры
и контрпримеры 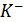 . При этом формируется логическая функция принадлежности к обобщенному понятию, которая служит классифицирующим правилом. В этой логической функции булевы переменные, отражающие значения признаков, соединены операциями конъюнкции, дизъюнкции и отрицания.
. При этом формируется логическая функция принадлежности к обобщенному понятию, которая служит классифицирующим правилом. В этой логической функции булевы переменные, отражающие значения признаков, соединены операциями конъюнкции, дизъюнкции и отрицания. , значение которой равно 1 на всех примерах из выборки
, значение которой равно 1 на всех примерах из выборки  , построение которого начинается с выбора среди элементов
, построение которого начинается с выбора среди элементов  , который является наиболее существенным для обобщенного понятия. Для выбранного признака ищется значение
, который является наиболее существенным для обобщенного понятия. Для выбранного признака ищется значение  , которое называют разделяющим значением, так как на его основе происходит разбиение выборок
, которое называют разделяющим значением, так как на его основе происходит разбиение выборок  и
и  ,
,  и
и  .
. ,
,  , …,
, …,  . Критерии
. Критерии  , служит частота появлений их в
, служит частота появлений их в 
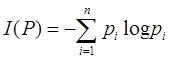
 .
.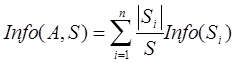 .
.



