Результат классификации в задаче MONK2(CN2)

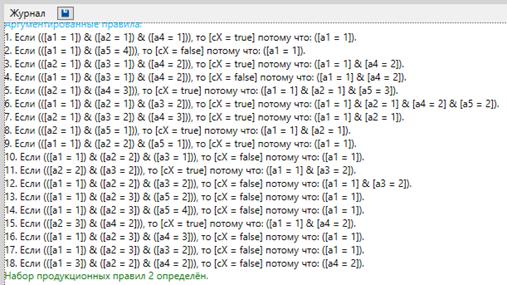
Вторая задача монахов связана с обучением понятию, которое можно описать с помощью следующего высказывания: «Если ровно два атрибута из шести для некоторого объекта принимают первое значение, то классифицировать этот объект как принадлежащий классу M 2». Обучающее множество состояло из 169 примеров (105 положительных и 64 отрицательных), что составляет 40% от полного пространства примеров. Множество тестовых примеров включало все возможные примеры (190 положительных и 242 отрицательных). Каждый объект характеризуется шестью условными атрибутами (области значений которых дискретны и включают малое число значений) и одним решающим атрибутом (с двумя классами решения).

Ниже представлен набор правил, сформированный на обучающем множестве задачи MONK2, а также результаты классификации.

Рис. 4.4 Результат обучения для набора данных MONK1

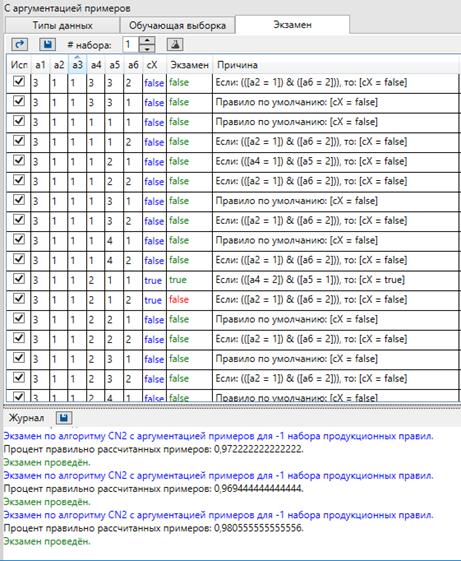
Рис. 4.5 Результаты опытов задачи MONK2.

Результат классификации в задаче MONK3(CN2)

Третья задача монахов заключается в том, чтобы описать понятие, которое задается с помощью следующего выражения: (a5 = 3 and a4 = 1) or (a5 /= 4 and a2 /= 3) Þ M 3. Обучающее множество состояло из 122 примеров (62 положительных и 60 отрицательных), что составляет 30% от полного пространства примеров. Множество тестовых примеров включало все возможные примеры (204 положительных и 228 отрицательных). Каждый объект характеризуется шестью условными атрибутами (области значений которых дискретны и включают малое число значений) и одним решающим атрибутом (с двумя классами решения). Следует отметить, что обучающее множество этой задачи содержит шум.

Рис.4.6 Набор правил для задачи MONK3.

Рис. 4.7 Результаты опытов задачи MONK3.

 

Средние результаты среди проведенных опытов с использованием алгоритма CN2: MONK1- 94.52%, MONK2- 66.24%, MONK3- 87.73%

 

Таблица 4.2 Результаты классификации известных алгоритмов обобщения

Набор данных	Точность классификации
ID3	C4.5	CN2	CART5	IDTUV
Glass	62.79	65.89	66.01	44.86	67.62
Monk-2	65.00	69.91	69.00	63.20	78.94
Australian	78.26	85.36	79.60	85.51	79.58
Monk-1	81.25	75.70	100.00	83.34	79.65
Adult	83.53	84.46	84.00	81.59	85.69
Monk-3	90.28	97.20	89.00	97.22	95.29
Iris	94.67	96.67	93.33	94.00	95.30
Anneal	99.55	91.65	98.60	97.87	99.55

 

 

В таблице 4.2 приведена информация о результатах работы некоторых известных алгоритмов на различных наборах данных.

Проанализировав результаты, полученные в ходе тестирования реализованного алгоритма CN2, можно заявить, что программа работает корректно. Алгоритм CN2 не уступает аналогичным алгоритмам обучения «с учителем»(например, алгоритму ID3) ни в построении достоверных решающих правил, ни в точности классификации новых примеров, а в некоторых случаях предоставляет даже наилучшее решение.

4.3. Оценка точности классификации примеров (с помощью алгоритма ABCN2)

В данном разделе проводится тестирование реализованного алгоритма ABCN2. Тестирование проводилось также на задачах монахов.

Результат обучения серьезно зависит от заданных экспертом аргументов. В зависимости от того, насколько правильно эксперт расставит приоритеты при задании того или иного аргумента будут меняться полученные аргументированные продукционные правила, а также результат классификации в целом.

Результат классификации в задаче MONK1(ABCN2)

Рис.4.8 Набор аргументационных правил для задачи MONK1.

 

Рис.4.9 Результат классификации в задаче MONK1.

Эксперт тщательно аргументировал примеры, на основании сводки правил из алгоритма CN2(Пример сводки правил - Рис.3.5). То есть, анализировались самые часто встречаемые правила, полученные при работе алгоритма CN2, и на основе них эксперт отдавал предпочтение или исключал тот или иной атрибут при аргументации. Были заданы аргументы «[cX= false] потому что [ x2 = 1]» и «[cX=false] потому что [ x 4 = x 5]». С помощью задания данных аргументов удалось увеличить процент классификации на 3-5% для каждого эксперимента, что говорит о том, что аргументация позволяет исключать противоречия, возникающие в ходе обычного обучения на зашумленных выборках и более эффективно проводить классификацию новых выборок.

 

Ниже представлены аналогичные результаты тестирования для задачи MONK3.