Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система отслеживания истинности выполняет по отношению к базе данных четыре функции.Содержание книги
Поиск на нашем сайте
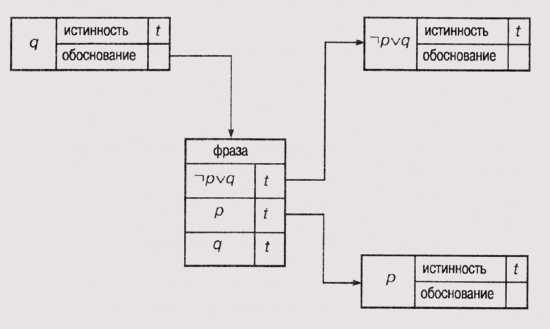
(1) Реализует множество дедукций высказываний, которые Мак-Аллестер назвал распространением пропозициональных принуждений (propositional constraint propagation). (2) Формирует обоснования при присвоении высказываниям значений истинности, когда такое присвоение выполняется в результате распространения принуждений (а не при установке значения пользователем). Таким образом, если мы приходим к заключению, что q истинно, поскольку истинны p и (p (3) Обновляет базу данных утверждений, как только какое-либо высказывание удаляется. Так, если мы приходим к выводу, что q истинно, поскольку истинны р и (p (4) Отслеживает цепочку предположений, которые привели к противоречию, с помощью метода, получившего наименование обратное прослеживание, ведомое зависимостями (dependency-directed backtracking). После этого пользователю предлагается удалить одно из предположений, "виновных" в появлении противоречия. Задавшись предположениями р и (— p v q) и пользуясь механизмом распространения принуждений, система отслеживания истинности может получить q. Затем она формирует поддерживающую структуру, представленную на рис. 19.2. Каждый узел в этой сети представляет собой фрейм (см. о фреймах в главе 6) с набором слотов, один из которых хранит наименование узла, другой — значение истинности, а третий — указатель на обоснование. Обоснование представлено другим фреймом, который содержит таблицу поддерживающих высказываний и их значения истинности. В структуре на рис. 19.2 истинность узла q подтверждается тем фактом, что узлы, представляющие р и (— p v g), отмечены как имеющие значения "истина". Обратите внимание на то, что узлы, представляющие предположения, как, например, р, не имеют указателей на фреймы обоснования, поскольку они полагаются истинными по определению. Если в дальнейшем окажется, что значение q несовместимо с содержимым остальной базы данных утверждений, то, анализируя описанную структуру данных, можно будет выйти на фреймы обоснования. После этого пользователю будет предоставлена возможность проследить цепочку зависимостей, связанную либо с р, либо с (-p v q). Для выполнения такого отслеживания очень важно, чтобы структуры поддержки были убедительными. Убедительность структуры означает отсутствие зацикливания, т.е. отсутствие такой ситуации, когда некоторое высказывание не подтверждает через "посредников" само себя. Обратите внимание — все утверждения являются либо предположениями, введенными пользователем, либо обосновываются наличием других утверждений. В следующем разделе мы рассмотрим другую, более сложную систему отслеживания истинности предположений, в которой допускается использовать в качестве обоснования отсутствие запрещающей информации.
Рис. 19.2. Структура представления связей между высказываниями Немонотонное обоснование Подход, предложенный Дойлом [Doyle, 1979], отличается от того, который применил Мак-Аллестер. Он основан на философии "здравого смысла", в частности на презумпции значения по умолчанию. В первом приближении, помимо хранения допущений, подтвержденных какими-либо свидетельствами, хранятся также допущения, основанные на резонном предположении, т.е. допущения, свидетельства против которых отсутствуют. Обоснования (или, пользуясь терминологией Доила, резоны) в пользу допущения Р представляют собой упорядоченную пару списков (IN P, OUT p ). Список IN p — обычные обоснования в форме, которая аналогична использованной Мак-Аллестером. Он содержит высказывания, истинность которых является необходимым условием истинности Р. Список OUT pсодержит высказывания, присутствие которых во множестве допущений указывает на ложность Р. Это множество получило название множества немонотонных обоснований (nonmonotonic justification), поскольку добавление высказывания в него потребует отказаться от сделанного ранее допущения. В подходе, который рассматривался Мак-Аллестером, этот вариант не анализировался. Пусть, например, обоснование для значения р имеет вид ({}, {-p}). Это означает, что можно предполагать наличие р до тех пор, пока это обоснование не станет ложным. Обоснование для q пусть имеет вид ({p}, {r}). Такое обоснование означает, что можно предполагать наличие q до тех пор, пока высказывание р присутствует в множестве текущих допущений (в терминологии Доила — получает статус поддержки (support status) "включено" — in), а высказывание rотсутствует в множестве допущений (в терминологии Доила — получает статус поддержки "исключено" — out). Обратите внимание на то, что обоснования могут быть связанными, как в приведенном выше примере. Если -р имеет статус исключено, то, следовательно, р имеет статус включено, а тогда и q имеет статус включено до тех пор, пока rимеет статус исключено. Такая цепочка причинно-следственных связей называется SL-обоснованием (SL — сокращение от support list). Общее правило для SL-обоснований гласит, что допущение Р присутствует в текущем множестве допущений только в том случае, если каждое из допущений, перечисленных в списке IN, имеет статус включено, а каждое из допущений, перечисленных в списке OUT, имеет статус исключено.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.108.134 (0.006 с.) |

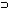 q), то р и (p
q), то р и (p