
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к решению задач по управлению качествомСодержание книги
Поиск на нашем сайте
Если в задаче требуется оценить пределы колебаний доли бракованной продукции, алгоритм решения следующий. Сначала оценивают долю (частость) бракованных изделий в выборочной совокупности:
где Далее рассчитывают среднюю ошибку выборки, которая показывает среднее расхождение между характеристиками выборочной и генеральной совокупности. Расчёт средней ошибки выборки зависит от вида отбора единиц в выборку. При повторном отборе (рисунок 6) каждая отобранная единица возвращается в генеральную совокупность и теоретически может снова быть отобрана в выборку. При бесповторном отборе (рисунок 7) каждая отобранная единица исключается из дальнейшего рассмотрения.
РИСУНОК 6 – Схема повторного отбора единиц в выборку
РИСУНОК 7 – Схема бесповторного отбора единиц в выборку
При повторном отборе средняя ошибка выборки для доли (частости) рассчитывается по формуле:
При бесповторном отборе средняя ошибка выборки для доли (частости) рассчитывается по формуле:
где n – число единиц выборки, N – число единиц генеральной совокупности. Дисперсия доли бракованной продукции по выборке рассчитывается по формуле:
где Если выборка достаточно велика (объем составлял не менее 20 единиц), то считается, что ошибка распределена по нормальному закону. Таким образом, зная закон распределения ошибки, можно определить предельную ошибку выборки и таким образом оценить границы интервала, за которые оценка доли бракованной продукции выйдет с заданной вероятностью (доверительной вероятностью). Такой интервал называется доверительным. Предельная ошибка определяется по формуле:
где
– коэффициент доверия. Коэффициент доверия определяется в зависимости от того, с какой доверительной вероятностью требуется гарантировать результаты выборочного исследования. Для определения
ТАБЛИЦА 9 – Наиболее часто встречающиеся значения коэффициента доверия
Таким образом, границы доверительного интервала могут быть представлены следующим образом:
где р – число бракованных изделий в генеральной совокупности.
Если в задаче требуется оценить необходимую численность выборки для оценки доли бракованных изделий при заданных параметрах, алгоритм решения следующий. Величина ошибки выборки зависит от численности выборочной совокупности При повторном отборе необходимая численность выборки определяется по формуле:
При бесповторном отборе необходимая численность выборки определяется по формуле:
где t – коэффициент доверия (определяется по таблице 9 в зависимости от заданной доверительной вероятности);
Решение типового примера. Произведено выборочное наблюдение для определения доли брака. В выборку было взято 800 изделий из общего количества в 6 тыс. изделий. В выборке было обнаружено 54 бракованных изделия. Определить размер колебания доли бракованных изделий в генеральной совокупности с вероятностью 0,954.
Определим долю дефектных изделий в выборке:
Определим дисперсию доли в выборочной совокупности:
Рассчитаем среднюю ошибку выборки:
Рассчитаем предельную ошибку выборки (t=2):
Определим границы доверительного интервала:
Таким образом, доля бракованных изделий в партии изделий с вероятностью 0,954 составляет от 6,11% до 7,39%.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.118.154 (0.01 с.) |

 , (15)
, (15)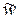 – доля бракованных изделий в выборочной совокупности;
– доля бракованных изделий в выборочной совокупности; 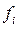 – число бракованных изделий; n – число единиц выборки.
– число бракованных изделий; n – число единиц выборки.
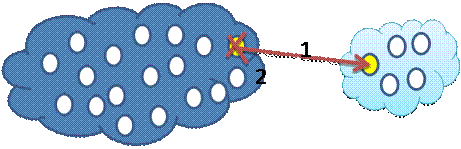
 (16)
(16) , (17)
, (17) - дисперсия доли бракованной продукции по выборке;
- дисперсия доли бракованной продукции по выборке; , (18)
, (18) - доля бракованных единиц в выборочной совокупности.
- доля бракованных единиц в выборочной совокупности. , (19)
, (19) – предельная ошибка выборки;
– предельная ошибка выборки;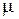 – средняя ошибка выборки;
– средняя ошибка выборки; пользуются таблицами нормального распределения. Некоторые наиболее часто встречающиеся значения этого коэффициента приведены в таблице 9.
пользуются таблицами нормального распределения. Некоторые наиболее часто встречающиеся значения этого коэффициента приведены в таблице 9. или
или  , (20)
, (20) . Задавая допустимую ошибку выборки, вероятность ошибки (через уровень доверительной вероятности), оценивая дисперсию изучаемого признака, можно определить численность выборки.
. Задавая допустимую ошибку выборки, вероятность ошибки (через уровень доверительной вероятности), оценивая дисперсию изучаемого признака, можно определить численность выборки. . (21)
. (21)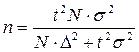 , (22)
, (22) – численность генеральной совокупности;
– численность генеральной совокупности; - дисперсия доли бракованной продукции по выборке (см. формулу 18);
- дисперсия доли бракованной продукции по выборке (см. формулу 18); .
. .
.
 .
.
 .
.


