
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтерактивні технології навчання та їх сутністьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ВСТУП Актуальність теми. У зв’язку із збільшенням розумового навантаження на уроках математики в старшій школі практикуються такі методичні прийоми, що підтримують в учнів інтерес до навчання, бажання займатися математикою, стимулюють їх активність протягом усього уроку. Одним із основних принципів діяльності викладача є принцип пріоритетного розвитку творчих здібностей дітей. За визначенням американського Е.Фромма, суть творчості – „ дивувати і пізнавати, це вміння знаходити рішення у нестандартних ситуаціях, це націленість на відкриття нового і здатності до глибокого пізнання особистого досвіду”. Як свідчать науково–педагогічні дослідження, здібності людини до певного виду діяльності розвиваються лише в процесі цієї діяльності. Можливості для такої діяльності учнів повинні створювати викладачі на уроках, і робити це потрібно спеціально. Спостереження засвідчують, що використання у навчальному процесі творчих завдань без систематичного навчання учнів того, як їх розв’язувати, допомагає розвинути творчі здібності лише у незначної частини школярів, найбільш обдарованих. Тому їх у процесі творчої діяльності потрібно систематично й цілеспрямовано навчати цієї діяльності. Викладачі дуже часто стикаються з проблемою зниження рівня пізнавальної активності учнів, небажанням працювати самостійно та й просто вчитися. Серед багатьох причин втрати дітьми інтересу до занять можна назвати одноманітність уроків. Відсутність можливості повсякденного пошуку нової, цікавої інформації призводить до шаблонного викладання, а це руйнує та вбиває дитячий інтерес до навчання. Творчий підхід учителя до побудови та проведення уроку, насиченість різноманітними прийомами, методами та формами викладання зможуть забезпечити його ефективність. Один із способів розвитку пізнавальної активності учнів — це використання інтерактивних технологій, які дають змогу підвищити активність і привернути увагу учнів до навчання.Урок з використанням інтерактивнихних технологій стає цікавішим для учня, а тому й ефективнішим для засвоєння знань. Стан дослідження проблеми. Інтерактивне навчання, його окремі складові досить ґрунтовно вивчалися такими науковцями, як: С. С. Кашлєв, М. В. Кларін, О. В. Козіна, О. А. Комар, О. І. Пометун, Г. О. Сиротенко, С. О. Сисоєва, Н. Суворова та ін. Інтерактивні технології на уроках математики розглядаються в працях Л. П. Ампілогової, Ж. Л. Бранопольської, В. В. Ковінчука, Л. Б. Новицької, Т. М. Паламар, Г. Скинець та ін. Ці дослідники приділяють значну увагу практичним аспектам інтерактивного навчання математики, наводять розробки уроків і фрагментів уроків із використанням інтерактивних форм і методів навчання. У своїй докторській дисертації М. Ф. Юсупова розглядає методику інтерактивного навчання графічних дисциплін студентів саме переважно в контексті відношень «студент– комп’ютер», «викладач–комп’ютер–студент». Деякі дисертаційні дослідження присвячені питанням упровадження окремих складових інтерактивного навчання як засобу розвитку учнів: О. О. Куликова (розвиток самостійності), С. М. Уткін (підвищення навченості). Інтерактивне навчання в площині певних конкретних дисциплін розглядалося такими дослідниками: Р. М. Абдулов (фізика, школа), Н. А. Коломієць (молодша школа), Л. М. Кратасюк (українська мова, середня школа), І. В. Куришева (природничо-наукові дисципліни, старша школа), І. Г. Луцик (суспільно- гуманітарний цикл, педагогічний коледж), Т. В. Сердюк (суспільні дисципліни, ВНЗ І–ІІ рівнів акредитації), О. О. Склярова (фізика, школа), Н. В. Солодюк (українська мова, старша школа), Н. С. Шолохова (фізика, середня школа), О. Є. Шувалова (географія, школа) та ін. Однак відкритими та недослідженими залишаються питання організації інтерактивного навчання саме уроків математики в старшій школі. Отже, актуальність і недостатність вивчення окресленої проблеми зумовили вибір теми курсової роботи: «Підвищення пізнавальної активності учнів на уроках математики шляхом використання інтерактивних технологій» Об’єкт дослідження – використання інтерактивних технологій на уроках математики. Предмет дослідження – шляхи формування пізнавальної активності учнів на уроці з використанням інтерактивних технологій. Для досягнення мети та розв’язання задач використано такі науково-педагогічні методи дослідження: вивчення та аналіз філософської, психологічної, педагогічної, методичної літератури, узагальнення одержаної інформації з метою дослідження особливостей використання інтерактивних технологій на уроках математики в старшій школі.
Поняття інтерактивна методика” та “інтерактивна технологія” Аналізуючи літературу, можна часто зустріти термін “інтерактивні технології навчання”, а не інтерактивні методи навчання. Розвиток науки та техніки пропонує учням та вчителям нові форми комунікації, нові типи розв’язання абстрактних і конкретних завдань, перетворюючи вчителя з авторитарного транслятора основних ідей на натхненника інтелектуального і творчого потенціалу учня. Майбутнє за системою навчання, що вкладалася б у схему учень – технологія – вчитель, за якої вчитель перетворюється на педагога-методолога, технолога, а учень стає активним учасником процесу навчання. На думку Аматьєва О. методична майстерність сучасного вчителя має розвиватися не через забазпечення його великою кількістю готових рецептурних посібників і широке використання ним готових поурочних розробок. Йому потрібні передусім фундаментальні знання з базового предмета, висока загальна культура і ґрунтовна дидактична компетентність. Вже на прчатку 20-х років минулого століття у працях відомих педагогів (І.П. Павлова, А.А. Ухтомського, С.Т. Шацького, В.М. Бехтєрєва) з’являються терміни “педагогічна технологія” й “педагогічна техніка”. Педагогічна техніка визначалась у педагогічній енциклопедії 1930-х років як сукупність прийомів і засобів, спрямованих на чітку й ефективну організацію навчальних занять. Відтоді минуло майже сто років, а в сучасній педагогічній літературі й досі не існує єдиних, вичерпних, уніфікованих визначень понять освітні, педагогічні, навчальні технології. Деякі дослідники налічують близько 300 дефініцій цих термінів, які різняться не лише за формою, а й за змістом, що в них вкладається. Одні науковці розуміють під терміном “технологія” управління педагогічними процесами, інші – способи організації діяльності учнів, різноманітні методи та прийоми досягнення педагогом навчальної мети тощо. На думку деяких дослідників, технологію від методики відрізняють два принципові моменти: гарантія остаточного результату й проектування майбутнього навчального процесу. Педагогічна технологія – набір процедур, які поновлюють професійну діяльність вчителя, і гарантують запланований остаточний результат. Технологія, на відміну від методики, не припускає варіативності, з неї не можна викинути жодного елемента. Для технологічного навчання обов’язковим є постійний зворотній зв'язок, коригування та зміни у подальшій діяльності.
Роль інтерактивних технологій у розвитку Правила дискусії (культура ведення дискусії). Дискусія дає прекрасну нагоду виявити різні позиції з певної проблеми або з суперечливого питання. Для того щоб дискусія була відвертою, необхідно створити в класі атмосферу довіри та взаємоповаги. Тому бажано знати правила культури ведення дискусії: 1. Говоріть по черзі, а не всі одночасно. 2. Не перебивайте того або той, хто говорить. 3. Критикуйте ідеї, а не особу, що її висловила. 4. Поважайте всі висловлені думки. 5. Не смійтеся, коли хтось говорить, за винятком, якщо хтось жартує. 6. Не змінюйте тему дискусії. 7. Намагайтеся заохочувати до участі в дискусії інших.
ВИСНОВКИ Інтерактивне навчання старшокласників математики – це таке навчання, за якого відбувається як взаємодія старшокласників з власним досвідом навчально-пізнавальної діяльності, так і з досвідом інших учнів (досвід усвідомлюється, акумулюється, систематизується); це таке навчання, сутність якого полягає в організації спільного процесу вчення, коли відбувається реалізація природної потреби старшокласників до діалогу, полілогу (комунікативно-діалоговий характер навчання) зі штучно побудованою системою, структура та зміст якої сприяють досягненню основної мети вивчення математики в старшій школі. При взаємодії учня з інтерактивним навчальним середовищем розвиваються такі якісні ознаки мислення як широта, самостійність, критичність, глибина, гнучкість мислення, широта розуму. За інтерактивного навчання математики старшокласники самостійно за допомогою спільного досвіду знаходять розв’язання тієї чи іншої задачі, через що не відбувається уніфікація алгоритму розв’язання будь- якої задачі. Таким чином, старшокласники при інтерактивному навчанні тренуються саме у власному мисленні, а не спостерігають мислення вчителя чи інших учнів, набувають власний досвід, обговорюють його з іншими, збагачуючи інших учнів власними ідеями щодо розв’язання певної проблемної ситуації.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ 1. Баханов К. О. Що ж таке технологія навчання? // Шлях освіти. – 1999. - №3.- 24 с. 2. Баханов К. О. Інноваційні системи, технології та моделі навчання історії в школі: Монографія – Запоріжжя: Просвіта, 2000. – 160 с. 3. Биков В. Ю. Моделі організації систем відкритої освіти: [монографія] / Валерій Юхимович Биков. – К.: Атика, 2008. – 684 с. 4. Воронцов В. В. Технология обучения // Педагогика / Под ред. П. И. Пидкасистого. – М.: 1996. – 168 с. 5. Інтерактивні технології навчання: теорія, практика, досвід: метод. Посіб. Уклад.: О. Пометун, Л. Пироженко. – К.: А.Н.Н., 2002. – 136 с. 6. Кашлев С. С. Интерактивные методы обучения: [учеб.-метод. пособие] / Сергей Семёнович Кашлев. – Минск: ТетраСистемс, 2013. – 224 с. 7. Кларин М. В. Интерактивное обучение – инструмент освоения нового опыта // Педагогика, 2000. - №7. – С. 12-18.ю 8. Козина Е. В. Польза от интерактивного обучения / Е. В. Козина // Здоровье детей. – 2005. – № 18. – С. 32–33. 9. Лапінський В. В. Навчальне середовище нового покоління та його складові [Електронний ресурс] / В. В. Лапінський. – Режим доступу: http://www.ii.npu.edu.ua/files/Zbirnik_KOSN/13/05.pdf. 10. Максимюк С. П. Педагогіка: Навчальний посібник. – К.: Кондор, 2005. – 667 с. 11. Педагогический энциклопедический словарь / [гл. ред. Б. М. Бим-Бад]. – М.: Большая российская энциклопедия, 2003. – 528 с. 12. Пометун О. І. Сучасний урок. Інтерактивні технології навчання: [наук. метод. посібн.] / О. І. Пометун, Л. В. Пироженко; за ред. О. І. Пометун. – К.: Видавництво А. С. К., 2004. – 192 с. 13. Селевко Г. К. Современные образовательные технологии: Учебное пособие. – М.: Народное образование, 1998. – 256 с. 14. Селевко Г. К. Энциклопедия образовательных технологий. В 2 т. Т. 1. М.: НИИ школьных технологий, 2006. – 816 с. 15. Сисоєва С. О. Інтерактивні технології навчання дорослих / С. О. Сисоєва // Рідна школа. – 2010. – № 11. – С. 3–8. 16. Сігіда Т. В. Орієнтація навчального середовища на формування особистості з цілісним мисленням / Т. В. Сігіда // Постметодика. – 2010.– № 5. – С. 34–37. 17. Суворова Н. Интерактивное обучение: новые подходы / Н. Суворова // Учитель. – 2000. – № 1. – С. 25–27. 18. Уткин С. М. Интерактивная педагогическая технология как фактор повышения обученности учащихся: дисс. … канд. пед. наук: 13.00.01 / Сергей Михайлович Уткин. – СПб, 2000. – 167 с. 19. Хуторской А. В. Современная дидактика. – С.-Петербург, 2001.- 553с. 20. Чернишова Ю. Интерактивные методы: обучение пониманию // Биология в школе, 1998.- №3. – С. 30-35. 21. Ярошенко О. Г. Групова навчальна діяльність школярів: теорія і методика. – К.: Партнер, 1997. – 193с.
ДОДАТКИ Додаток А Нетрадиційний урок. Урок – змагання.
Тема уроку: Розв’язування нерівностей. Мета уроку: Перевірити якість знань і вмінь учнів при розв’язуванні тригонометричних, показникових та логарифмічних нерівностей; розвивати увагу, пам'ять, кмітливість, логічне мислення, виховувати почуття колективізму, відповідальності, інтересу до предмета.
Хід уроку.
І. Вступне слово вчителя. Учні поділені на 4 команди. Кожна має свою назву та виготовлені емблеми. Умови гри: потрібно відгадати слово – код, ключем до нього є правильний розв’язок нерівності. Гра проводиться в 3 етапи: І етап: Розв’язування тригонометричних нерівностей:
1.
2. cos х < - 3.
ІІ етап: Розв’язування показникових нерівностей:
4. 2х > 8 (А) (В: (3; +
5. (
6. 2х2 > (
ІІІ етап: Розв’язування логарифмічних нерівностей:
7. log 5 х > log 5 12 (Б) (12; +
8. log ½ х < log ½ 4 (Б) (4;
9. log 5 (3х + 1) > 2 (А) (8;
Примітка: Перші два завдання кожного етапу оцінюються в 0,5 бала, третє завдання - 2 бали.
Команда може набрати максимально 12 балів і отримає шукане слово – код ФЛЕКСАГОН – це многокутник, складений із смужки прямокутної або більше складної зігнутої форми, що володіє дивовижною властивістю: при перегинанні флексагона його зовнішня поверхня ховається всередину, а попередню схована поверхня несподівано виходить наверх.
А тепер супер – гра: Задача: Розв’язування рівняння: 2 cos
2 cos
можлива лише при 5х +
тобто при х = 6 5х = 1 Звідси х = 0 Оголошується команда - переможець. Оцінки за роботу на уроці виставляє капітан команди для своїх учасників. Потім ці оцінки узгоджують капітани з викладачем.
Додаток Б Хід уроку. І. Перевірка домашнього завдання. Актуалізація опорних знань. Дати відповіді на запитання: 1. Означення оборотної функції. 2. Як визначити чи функція оборотна чи ні? 3. Означення оберненої функції, її область визначення і область значень. 4. Оборотна функція у = f (х) задана формулою. Як утворити обернену функцію g? Перевірка домашнього завдання. Скласти обернену функцію
Відповідь: g (х) =
ІІ. Сприймання і усвідомлення понять логарифмічної функції, засвоєння властивостей логарифмічної функції та її графіка (використання бумеранга). Розглянемо показникову функцію у = ах та пригадаємо її властивості (таб. 1 “Властивості показникової функції у = ах ”)
- Чи можна функцію у = ах вважати оборотною? Пояснити це. - Вивести формулу, що задає функцію g, обернену до f (х) = ах у = ах, х = ау, у = log а х.
Означення: Функцію, яку можна задати за допомогою формули у = log а х називають логарифмічною. Властивості логарифмічної функції у = log а х.
1. D (log а) = R+ (0; 2. Е (log а) = R (- 3. Логарифмічна функція на всій області визначення зростає, якщо а > 1 і спадає якщо 0 < а < 1 (з теореми про обернену функцію). 4. Побудова графіка функції у = log а х, якщо а > 1 і 0 < а < 1 (графіки будуються за властивістю оберненої функції).
Рис. 1
Для логарифмічної функції притаманні всі властивості логарифмів: 5. Для будь-якого а > 1 (а = 1) виконуються рівності: 1. log а 1 = 0; 2). log аа = 1; 3. log а(ху) = log ах + log ау; якщо х > 0; у > 0.
4. log а ( 5. Для будь-якого числа х > 0 і р є R log ахр = р log ах
ІІІ. Тренувальні вправи.
Розв’яжемо вправи, де використовуються властивості логарифмічної функції.
Завдання 1: Знайти область визначення функції: 1. f (х) = log8 (4 – 5х) 4 – 5х > 0; -5х > -4; х < 0.8 В: D (f) = (- 2. f (х) = log2 (х2 – 3х - 4) D = 25, х1 = - 1; х2 = 4 Відповідь: D (f) = (-
3. у = lg (16 – х2) 16 – х2 > 0; (4 – х) (4 + х) > 0 Відповідь: D (f) = (-4; 4)
4. у = log ½ (5х – х2 – 6) Відповідь: D (f) = (-2; 3) Завдання 2 (усно)
Рис. 2
Висновок: Крива тим ближче прилягатиме до осі Х, чим більше а (а > 1). Крива тим щільніше до осі, чим менше а (0 < а < 1)
Щоб розв’язати наступне завдання, вам необхідно взяти з папки “Вчись вчитись” властивості логарифмів.
Завдання 3 (усно: рис. 2)
1. Який висновок можна зробити щодо додатних чисел m і n, якщо log5 m < log5 n? (Відповідь m < n)
2. Який висновок можна зробити щодо додатного числа m, якщо log4 m = - 3.7? (Відповідь m < 1)
3. Який висновок можна зробити щодо додатних чисел m і n, якщо log ½ m > log ½ n? (Відповідь m < n)
Завдання 4 (усно) За властивостями логарифмічної функції визначити, що більше: 1) log2 3 чи log2 5 (В.: log2 5 > log2 3) 2) log1/2 5 чи log1/2 3 (В.: log1/2 3 > log1/2 5) 3) log2 1 чи log7 1 (В.: log2 1 = log7 1) 4) log3 3 чи log5 5 (В.: log3 3 = log5 5) 5) log0.32 чи log5 3 (В.: log5 3 > log0.3 2) 6) log4 5 чи log5 4 (В.: log4 5 > log5 4)
Завдання 5. Знайти помилку в міркуваннях:
( Відповідь: із нерівності 2 lg
ІV. Домашнє завдання.
V. Підсумок уроку.
Додаток В Хід уроку. ІІІ. “Робота в парах”.
№ 1. Оборіг для зберігання сіна має форму правильної чотирикутної призми з пірамідальним верхом. Висота оборогу 5 м, причому висота його частини, що має форму призми становить 3 м., а сторона основи – 6 м. Густина сіна 30 кг/м3. Який об’єм оборогу? Скільки кілограм сіна вміщається під оборогом? Чи вистачить цього сіна для годівлі 2-х корів, що з’їдають в день 20 кг на зимово-стійловий період з 15 жовтня по 7 травня?
№ 2. Цистерна для зберігання дизельного палива має форму циліндра з двома боковими півкулями. Діаметр циліндра – 2 м, а його довжина – 3 м. Скільки літрів дизельного палива вміщається в цистерну? На скільки днів вистачить цього дизельного палива для щоденної повної заправки трактора МТЗ-80 (місткість паливного бака трактора МТЗ-80 становить 120 літрів)?
ІV. Підсумок уроку.
ВСТУП Актуальність теми. У зв’язку із збільшенням розумового навантаження на уроках математики в старшій школі практикуються такі методичні прийоми, що підтримують в учнів інтерес до навчання, бажання займатися математикою, стимулюють їх активність протягом усього уроку. Одним із основних принципів діяльності викладача є принцип пріоритетного розвитку творчих здібностей дітей. За визначенням американського Е.Фромма, суть творчості – „ дивувати і пізнавати, це вміння знаходити рішення у нестандартних ситуаціях, це націленість на відкриття нового і здатності до глибокого пізнання особистого досвіду”. Як свідчать науково–педагогічні дослідження, здібності людини до певного виду діяльності розвиваються лише в процесі цієї діяльності. Можливості для такої діяльності учнів повинні створювати викладачі на уроках, і робити це потрібно спеціально. Спостереження засвідчують, що використання у навчальному процесі творчих завдань без систематичного навчання учнів того, як їх розв’язувати, допомагає розвинути творчі здібності лише у незначної частини школярів, найбільш обдарованих. Тому їх у процесі творчої діяльності потрібно систематично й цілеспрямовано навчати цієї діяльності. Викладачі дуже часто стикаються з проблемою зниження рівня пізнавальної активності учнів, небажанням працювати самостійно та й просто вчитися. Серед багатьох причин втрати дітьми інтересу до занять можна назвати одноманітність уроків. Відсутність можливості повсякденного пошуку нової, цікавої інформації призводить до шаблонного викладання, а це руйнує та вбиває дитячий інтерес до навчання. Творчий підхід учителя до побудови та проведення уроку, насиченість різноманітними прийомами, методами та формами викладання зможуть забезпечити його ефективність. Один із способів розвитку пізнавальної активності учнів — це використання інтерактивних технологій, які дають змогу підвищити активність і привернути увагу учнів до навчання.Урок з використанням інтерактивнихних технологій стає цікавішим для учня, а тому й ефективнішим для засвоєння знань. Стан дослідження проблеми. Інтерактивне навчання, його окремі складові досить ґрунтовно вивчалися такими науковцями, як: С. С. Кашлєв, М. В. Кларін, О. В. Козіна, О. А. Комар, О. І. Пометун, Г. О. Сиротенко, С. О. Сисоєва, Н. Суворова та ін. Інтерактивні технології на уроках математики розглядаються в працях Л. П. Ампілогової, Ж. Л. Бранопольської, В. В. Ковінчука, Л. Б. Новицької, Т. М. Паламар, Г. Скинець та ін. Ці дослідники приділяють значну увагу практичним аспектам інтерактивного навчання математики, наводять розробки уроків і фрагментів уроків із використанням інтерактивних форм і методів навчання. У своїй докторській дисертації М. Ф. Юсупова розглядає методику інтерактивного навчання графічних дисциплін студентів саме переважно в контексті відношень «студент– комп’ютер», «викладач–комп’ютер–студент». Деякі дисертаційні дослідження присвячені питанням упровадження окремих складових інтерактивного навчання як засобу розвитку учнів: О. О. Куликова (розвиток самостійності), С. М. Уткін (підвищення навченості). Інтерактивне навчання в площині певних конкретних дисциплін розглядалося такими дослідниками: Р. М. Абдулов (фізика, школа), Н. А. Коломієць (молодша школа), Л. М. Кратасюк (українська мова, середня школа), І. В. Куришева (природничо-наукові дисципліни, старша школа), І. Г. Луцик (суспільно- гуманітарний цикл, педагогічний коледж), Т. В. Сердюк (суспільні дисципліни, ВНЗ І–ІІ рівнів акредитації), О. О. Склярова (фізика, школа), Н. В. Солодюк (українська мова, старша школа), Н. С. Шолохова (фізика, середня школа), О. Є. Шувалова (географія, школа) та ін. Однак відкритими та недослідженими залишаються питання організації інтерактивного навчання саме уроків математики в старшій школі. Отже, актуальність і недостатність вивчення окресленої проблеми зумовили вибір теми курсової роботи: «Підвищення пізнавальної активності учнів на уроках математики шляхом використання інтерактивних технологій» Об’єкт дослідження – використання інтерактивних технологій на уроках математики. Предмет дослідження – шляхи формування пізнавальної активності учнів на уроці з використанням інтерактивних технологій. Для досягнення мети та розв’язання задач використано такі науково-педагогічні методи дослідження: вивчення та аналіз філософської, психологічної, педагогічної, методичної літератури, узагальнення одержаної інформації з метою дослідження особливостей використання інтерактивних технологій на уроках математики в старшій школі.
Інтерактивні технології навчання та їх сутність
Процес навчання – не автоматичне вкладання навчального матеріалу в голову учня. Адже куди важливіше навчити, ніж просто розповісти. Цей процес потребує напруженої розумової роботи підлітка та його власної активної участі в цьому процесі. Цю мету і переслідує застосування інтерактивних технологій. Інтерактивні технології – це порівняно новий, творчий, цікавий підхід до організації навчальної діяльності учнів. Слово “інтерактив” походить від англійського слова “interact”. “Inter” – це взаємний, “act” – діяти. Інтерактивний – здатний взаємодіяти або перебувати в режимі бесіди, діалогу з будь-чим (наприклад, комп’ютером) або з будь-ким (людиною). Сутність інтерактивного навчання полягає в активному залученні всіх учнів до процесу пізнання. У педагогічній літературі описано чимало типів організації навчання (за рівнем активності учнів, рівнем залучення їх до продуктивної діяльності, за дидактичною метою, за способами організації тощо). Голант Е.Я. (60-ті рр.) поділив типи та методи навчання на активні та пасивні залежно від участі учнів у навчальній діяльності. Звісно, термін “пасивне” є умовним, адже будь-яка організація навчального процесу неодмінно передбачає певний рівень пізнавальної активності суб’єкта – учня, інакше досягнення навіть мінімального результату неможливе. У своїй класифікації Я. Голант використовує “пасивність” як визначення низького рівня активності учнів, переважно репродуктивної діяльності за майже цілковитої відсутності самостійності й творчості. До цієї класифікації ми додамо інтерактивне навчання як різновид активного, котрий, однак, має свої закономірності та особливості. При пасивному типі навчання учень виступає у ролі “об’єкта” навчаня, має засвоїти й відтворити матеріал, переданий йому вчителем, текстом підручника тощо – тобто джерелом правильних знань. До відповідних методів навчання належать методи, що вимагають від учнів лише слухати й дивитися (лекція-монолог, читання, пояснення, демонстрація й відтворювальне опитування учнів). Учні, як правило, не спілкуються один з одним і не виконують жодних творчих завдань. При активному навчанні передбачається застосування методів, що стимулюють пізнавальну активність і самостійність учнів. Учень виступає “суб’єктом” навчання, виконує творчі завдання, вступає у діалог з вчителем. Основними методами цього навчання є: самостійна робота, проблемні й творчі завдання, питання учня до вчителя і навпаки, що розвивають творче мислення. Сутність інтерактивного навчання полягає в тому, що навчальний процес відбувається за умов постійної, активної взаємодії всіх учнів. Це співнавчання, взаємонавчання (колективне, групове, навчання в співпраці), де учень і вчитель є рівноправними, рівнозначними суб’єктами навчання. Педагог виступає в ролі організатора процесу навчання, лідера групи. Організація інтерактивного навчання передбачає моделювання життєвих ситуацій, використання рольових ігор, спільне розв’язання проблем. Воно ефективно сприяє формуванню цінностей, навичок і вмінь, створенню атмосфери співпраці, взаємодії, дає змогу педагогу стати справжнім лідером учнівського колективу. Отже, інтерактивні технології – це організація засвоєння знань і формування певних вмінь та навиків через сукупність особливим способом організованих навчально-пізнавальних дій, що полягають у активній взаємодії учнів між собою та побудові міжособистісного спілкування з метою досягнення запланованого результату. Дослідження проведені Національним тренінговим центром (США, штат Меріленд) у 1980-х роках, засвідчують, що інтерактивне навчання вможливлює різке збільшення відсотка засвоєння матеріалу, бо впливає не лише на свідомість учня, а й на його почуття, волю. Результати цих досліджень відображено у схемі, яка дістала назву “Піраміда навчання”. “Піраміда навчання” демонструє, що найменших результатів можна досягти за умов пасивного навчання (лекція – 5%, читання – 10%), а найбільших – інтерактивного(дискусійні групи – 50%, практика через дію – 75%, навчання інших або негайне застосування знань – 90%). Ці дані є середньостатистичними, тому у конкретних випадках результати можуть різнитися, але в середньому таку закономірність може простежити кожен педагог. Науковці виділяють наступні принципи інтерактивного навчання: 1. Принцип активності. Означає, що для досягнення поставлених цілей кожен учень повинен брати активну участь у процесі спілкування та активно взаємодіяти з іншими. 2. Принцип відкритого зворотнього зв’язку, сутність якого полягає в обов’язковому висловленні членом чи всіма членами групи думок, ідей чи заперечень щодо поставлених завдань. Саме завдяки активному використанню зворотнього зв’язку учасники групи довідуються, як сприймаються іншими людьми їхня манера спілкування, стиль мислення, особливості поведінки. Завдяки цьому принципу відбувається корекція мовлення. 3. Принцип експериментування припускає активний пошук учнями нових ідей та шляхів вирішення поставлених завдань. Цей принцип дуже важливий і як зразок стратегії поводження в реальному житті, і як поштовх до розвитку творчості й ініціативи особистості. 4. Принцип довіри в спілкуванні. Саме на це спрямовано спеціальну організацію групового простору в ході проведення занять: звичайно використовуваний у роботі прийом розташування учня і вчителя по колу обличчям один до одного, для того щоб змінити в учнів стереотипну установку і уявлення про те, як повинні проводитися й організовуватися заняття і яку роль у них повинен грати вчитель. 5. Принцип рівності позицій. Він означає, що вчитель не прагне нев’язати учням своєї думки, а діє разом з ними. В свою чергу, учень має змогу побувати у ролі організатора, лідера. Нагромаджений вже сьогодні в Україні та за кордоном досві переконливо засвідчує, що інтерактивні технології сприяють інтенсифікації та оптимізації навчального процесу. Вони дозволяють учням: - аналізувати навчальну інформацію, творчо підходити до засвоєння навчального матеріалу й тому зробити засвоєння знань більш доступним; - навчитись формулювати власну думку, правильно її виражати, доводити власну точку зору, аргументувати й дискутувати; - навчитись слухати іншу людину, поважати альтернативну думку; - моделювати різні соціальні ситуації, збагачувати власний соціальний досвід через включення в різні життєві ситуації; - вчитись будувати конструктивні відносини в групі, визначати своє місце в ній, уникати конфліктів, розв’язувати їх, шукати компроміси, прагнути діалогу; - знаходити спільне розв’язання діалогу; - розвивати навички проектної діяльності, самостійної роботи, виконання творчих робіт.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 634; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.019 с.) |

 sin x
sin x 
 (С) (В:
(С) (В:  + 2
+ 2  n
n  х
х  + 2
+ 2  (В: О) Л
(В: О) Л tg 2 х
tg 2 х  +
+  n
n  +
+  )) К
)) К )х
)х  (Б) (В: (3;
(Б) (В: (3;  = 5х + 5-х
= 5х + 5-х х
х 
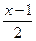

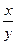 ) = log ах - log а у, якщо х > 0; у > 0.
) = log ах - log а у, якщо х > 0; у > 0.
 )2 > (
)2 > (


