
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: треугольник и его элементы.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Тема: Треугольник и его элементы. ЦЕЛИ: 1. Изучить понятие треугольника и его элементов в ходе практической работы; 2. Развитие логического мышления учащихся. Формирование устойчивого познавательного интереса к изучению геометрии. 3. Воспитание отношений взаимопомощи и сотрудничества между учащимися в процессе познавательной деятельности; развитие их самостоятельности и творчества. ХОД УРОКА Организационный момент. Мотивация урока. Кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? (Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида). А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного. Зовётся он треугольник, И с ним хлопот не оберётся школьник! Актуализация опорных знаний. Среди множества различных геометрических фигур на плоскости выделяется большое семейство МНОГОУГОЛЬНИКОВ. Названия геометрических фигур имеют вполне определенный смысл. Присмотритесь внимательно к слову “многоугольник”, и скажите из каких частей оно состоит. Слово “многоугольник” указывает на то, что у всех фигур этого семейства “много углов”. Подставьте в слово “многоугольник” вместо части “много” конкретное число, например 5. Вы получите ПЯТИУГОЛЬНИК. Или 6. Тогда – ШЕСТИУГОЛЬНИК. Заметьте, сколько углов, столько и сторон, поэтому эти фигуры вполне можно было бы назвать и многосторонниками. На рисунке геометрические фигуры. Используя рисунок, назовите эти фигуры.
Каким наименьшим числом можно заменить “много” в многоугольнике? (Ответ: 3) Изучение нового материала. Часто знает и дошкольник, Что такое треугольник, А уж вам-то, как не знать… Но совсем другое дело — Очень быстро и умело Треугольники считать! Например, в фигуре этой Сколько разных? Рассмотри! Все внимательно исследуй И “по краю” и “внутри”.
Треугольник – простейшая фигура: три стороны, три вершины, три угла. Математики называют его двумерным “симплексом” - по латыни означает простейший. Именно в силу своей простоты треугольник явился основой многих измерений. Через площадь треугольника выражается площадь любого многоугольника, достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Еще 4000 лет назад в одном египетском папирусе говорилось о площади треугольника. Через 2000 лет в Древней Греции очень активно велось изучение свойств треугольника. Пифагор открыл свою знаменитую формулу. Особенно плодотворно свойства треугольника исследовались в XV-XVI веках. Большой вклад в эту теорию внес знаменитый математик Леонард Эйлер. Император Франции Наполеон свободное время посвящал занятием математики и, в частности, изучению свойства треугольников.
ТРЕУГОЛЬНИК – геометрическая фигура, состоящая из трех точек (вершин) и трех попарно соединяющих их отрезков (стороны). Задача Земельный участок имеет треугольную форму. Сколько потребуется метров проволоки, чтобы обнести этот участок забором? (Ответ: измерить стороны и сложить их длины.) Как мы называем сумму длин всех сторон треугольника? (Ответ: периметр.) Р = АВ + ВС + СА (ед.) Практическая работа. Медиана. Начертите треугольник АВС и найдите середину стороны ВС – точку М. Что называется серединой отрезка? (Серединой отрезка называется точка отрезка, которая делит его пополам, то есть на два равных отрезка). Запись на доске: АМ=МС. Соедините точку М с вершиной В. Отрезок ВМ называется медианой треугольника. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Сколько вершин у треугольника? (3). Сколько у него сторон? (3). Сколько медиан можно провести в треугольнике?(3). “Проведите” три медианы на моделях треугольников. Какое свойство медиан вы заметили? В любом треугольнике все медианы пересекаются в одной точке. Эта точка называется центром тяжести треугольника. Высота. Запись на доске: ВН С помощью чертёжного угольника из вершины В треугольника АВС проведём перпендикуляр ВН к прямой АС. Он называется высотой треугольника. Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону. Сколько высот имеет треугольник? (3). “Постройте” все три высоты на модели вашего треугольника. Обладают ли высоты аналогичным свойством, что и медианы? (Да). Высоты или их продолжения пересекаются в одной точке. Биссектриса. Вспомните определение биссектрисы угла. Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла. Запись на доске: Постройте биссектрису ВК угла В с помощью транспортира. Она пересечёт отрезок АС в точке К. Отрезок ВК называется биссектрисой угла В треугольника АВС. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны треугольника. Покажите все три биссектрисы на вашей модели треугольника. Сформулируйте свойство биссектрис треугольника. В любом треугольнике биссектрисы пересекаются в одной точке. Классификация треугольников. По величине углов 1). Остроугольные. 2). Прямоугольные. 3). Тупоугольные. По длине сторон: · Разносторонние. · Равнобедренные. · Равносторонние. “ Перпендикуляр” - от латинского слова “PERPENDICULARIS” - “отвесный”. Термин был образован в средние века. “ Биссектриса” - от латинских слов (дважды, надвое) и “SECTRIX” - “секущая”. “ Медиана” - от латинского слова “MEDIANA” - “средняя” (линия). Итоги урока. Рефлексия. Что больше всего тебе запомнилось на уроке? Что удивило? Что понравились больше всего? Каким ты хочешь увидеть следующий урок? Домашнее задание: выучить п.9, вопросы с.77, решить № 263, 269(б), 262. (творческое): · Сочинить рассказ, сказку или стихотворение о стране треугольников. · Составить картинку из различных видов треугольников.
ХОД УРОКА Организационный момент. Мотивация урока. Изучение нового материала. Практическое задание. Измерить с помощью транспортира углы треугольников (остальным учащимся модели треугольников заранее раздать) и найти их сумму.(каждый ученик говорит свой результат) Что получилось? Сумма углов треугольника равна 180°? Выскажите гипотезу. «Сумма углов любого треугольника равна 180°» Гипотеза сформулирована. Чтобы она стала истиной – требуется доказать. Итак, теорема Формулировка: Сумма углов треугольника равна 180° Дано: Доказать:
1)Проведём DE ׀׀ AC.
3)
4) Впервые доказал теорему Пифагор, затем Евклид. Закрепление теоремы в ходе устных упражнений по готовым чертежам.
Введение понятия внешнего угла треугольника. Внешним углом треугольника называется угол, смежный с внутренним углом треугольника. Свойство внешнего угла треугольника: внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Физкультминутка. Одолела вас дремота, (Зеваем.) Шевельнуться неохота? Ну-ка, делайте со мною Упражнение такое: Вверх, вниз потянись, (Руки вверх, потянулись.) Окончательно проснись. Руки вытянуть пошире. (Руки в стороны.) Раз, два, три, четыре. Наклониться — три, четыре (Наклоны туловища.) И на месте поскакать. (Прыжки на месте.) На носок, потом на пятку. Все мы делаем зарядку. Самостоятельная работа. Тренировочный тест по готовым чертежам. 1.Найдите
4.Найдите Итоги урока. Д/з.
Вот и подошел к концу наш урок. Давайте подведем итоги. Мы выучили - …. Мы умеем - … Сделаем выводы - ….
Тема: Равные треугольники. Цели урока:
ХОД УРОКА Организационный момент. Мотивация урока. Изучение нового материала. -Как можно сравнить два прямоугольника? (Чтобы сравнить два прямоугольника, надо один прямоугольник наложить на другой, если из-за верхнего прямоугольника будет виден нижний, значит верхний прямоугольник меньше нижнего и наоборот. А если они совместятся, то данные прямоугольники равны.) – Как сравнить два треугольника, изображенных на доске (внешне два треугольника должны быть почти равными)? (Скопировать один треугольник на прозрачный материал, например на кальку, и наложить на второй.) – Какие две геометрические фигуры можно назвать равными? (Две геометрические фигуры называются равными, если при наложении они совмещаются) Фигуры называются равными, если при наложении совпадают. Справка из истории: Если мы обратимся к истории, то в самом первом учебнике по геометрии “Началах” Евклида можно найти следующее определение: “…Совмещающиеся друг с другом равны между собой…” Прошло столько лет, а определение практически не изменилось. Эти определения о равенстве фигур можно отнести и к треугольникам, так как треугольник это фигура.
Историческая пауза. Треугольник - самая простая замкнутая прямолинейная фигура, одна из первых, свойства которой человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни. В строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Изображение треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и в других древних документах. В древней Греции учения о треугольниках развивалось в ионийской школе, основанной в VII веке до н.э. Фалесом, в школе Пифагора число три определялось через треугольник. Три - треугольник, образующий плоскость двух измерений, и возврат к определенности. Числа пифагорийцы изображали в виде точек, известны, так называемые, треугольные числа (1, 3, 6, 10...), которые образуют правильный треугольник. Учение о треугольниках было полностью изложено в первой книге “Начал” Евклида. Среди определений, которыми начинается эта книга, имеются и следующие: ”Из трехсторонних фигур равносторонний треугольник есть фигура, имеющая три равных стороны, равнобедренный же - имеющая только две равные стороны, разносторонний - имеющая три неравные стороны”. Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники. Самостоятельная работа. Решить № 338. Итоги урока. Д/з. Выучить п.11, вопросы с.89. Решить № 329. 332, 301. ХОД УРОКА Организационный момент. Мотивация урока. Три пути ведут к знаниям: путь размышления - это путь самый благородный, путь подражания - это путь самый легкий и путь опыта - это путь самый горький. Какой путь выберите вы? 3. Актуализация опорных знаний. Теоретический опрос по вопросам: · объясните, какая фигура называется треугольником; · начертите треугольник и покажите его стороны вершины и углы; · что такое периметр треугольника? · какие треугольники называются равными?
Назовите углы: а) Углы ∆DEK, прилежащие к стороне ЕК; б) углы ∆MNP, прилежащие к стороне MN. Назовите угол: а) ∆DEK, заключенный между сторонами DE и DК; б) ∆MNP, заключенный между сторонами NP и РМ. Между какими сторонами: а) ∆DEK заключен угол К; б) ∆MNP заключен угол N?
∆АВС= ∆КМР. Назовите равные стороны и равные углы этих треугольников.
Изучение нового материала. Какие треугольники равны?- Но всегда ли нам удаётся реально совместить треугольники? (Нет) - Действительно, иногда совместить треугольники нет возможности. Что же делать? Достаточно сравнить лишь три элемента одного треугольника с тремя элементами другого треугольника. Вот тут нам на помощь придут признаки равенства треугольников, они нам расскажут, какие именно элементы нужно сравнивать. Что такое признак равенства треугольников и сколько существует признаков? Некоторые условия, при которых два данных треугольника оказываются равными, называются признаками равенства треугольников. Можно сказать, что признак – это примета, по которой можно узнать те или иные свойства фигур. - Сегодня на уроке мы познакомимся с первым и вторым признаками равенства треугольников. Первый признак равенства треугольников. Физминутка Почти 90%всей информации человек воспринимает глазами. Если устают глаза, снижается наше внимание и активность. Давайте перед следующей задачей дадим отдых глазам и себе. 1. Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы. Повторите 3-4 раза. 2. Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 3-4 раза. 3. Медленно наклоняйте голову: вперед – влево – вправо - назад. Повторите 3-4 раза. 4. Поморгайте несколько раз глазами, не напрягая мышц. Сделайте глубокий вздох и медленный выдох. Итоги урока. Д/з. - Что нового вы узнали сегодня на уроке? С чем познакомились? Сформулируйте первый и второй признаки равенства треугольников? Помогли ли они вам при решении задач? Ребята, математика наука точная, поэтому все определения и теоремы воспроизводить своими словами нельзя? Послушайте одну старинную историю. Это произошло в те времена, когда на улицах городов еще не было освещения. Как-то ночью мэр столкнулся с горожанином. Это было неприятно и больно. Тогда мэр отдал приказ, чтобы никто не выходил ночью на улицу без фонаря. Следующей ночью мэр опять столкнулся с тем же горожанином. - Вы не читали моего приказа? — спросил мэр сердито. - Читал, — ответил горожанин. — Вот мой фонарь. - Но в фонаре у вас нет ничего. - В приказе об этом не упоминалось. Наутро появился новый приказ, обязывающий вставлять свечу в фонарь при выходе ночью на улицу. Вечером мэр опять налетел на того же горожанина, - Где фонарь?! — закричал мэр. - Вот он. - Но в нем нет свечи! - Нет, есть. Вот она. - Но она не зажжена! - В приказе ничего не сказано о том, что надо зажигать свечу. И мэру пришлось издать еще один приказ, обязывающий граждан зажигать свечи в фонарях при выходе ночью на улицу. Вот почему следует формулировки определений, аксиом и теорем учить наизусть. Если вы можете своими словами передать их точный смысл — пожалуйста! Если же нет, то, чтобы не уподобляться тому мэру, о котором только что услышали, следует учить наизусть. Выучить п.12, решить № 355, 357, 364.
ХОД УРОКА Организационный момент. Мотивация урока. Можно сказать, что почти вся геометрия со времен “Начал” Евклида покоится на “трех китах” - трех признаках равенства треугольников. Лишь на рубеже ХIХ - ХХ в.в. математики научились строить геометрию на основе более фундаментального и общего, чем равенство треугольников, понятия геометрического преобразования. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о “геометрии треугольника” как о самостоятельном разделе элементарной геометрии. И сегодня мы продолжить работать над закреплением первого и второго признаков равенства треугольников. Физкультминутка Что такое физкультура? Тренировка и игра. Что такое физкультура? Физ и куль и ту и ра! Руки вверх, руки вниз – это физ. Крутим шею, словно руль – это куль. Ловко прыгай в высоту – это ту. Бегай пол часа с утра – это Ра. Занимаясь этим делом, Станешь сильным, ловким, смелым. Плюс – хорошая фигура. Вот что значит физкультура! На четыре - руки шире, Пять – руками помахать. Шесть – за парту тихо сесть. Самостоятельная работа. Решить № 2, 3 (вариант 3). с.99. Итоги урока. Д/з. Решить вариант 1 (вариант 2) с.99. ХОД УРОКА Организационный момент. Мотивация урока. Треугольник - самая простая замкнутая прямолинейная фигура, одна из первых, свойства которой человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни. В строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Изображение треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и в других древних документах. И сегодня нам предстоит познакомиться с одним из его представителей. Изучение нового материала. Учитель демонстрирует рисунки с изображениями треугольников (плакаты):
Какой особенностью обладают эти треугольники? Учащиеся замечают равные стороны (или углы). Учитель дает определение равнобедренного треугольника, показывает его основание и боковые стороны. Вопрос: дать определение равнобедренного треугольника. Практическое задание: построить равнобедренный треугольник ABC (BC – основание) на нелинованной бумаге (учитель выполняет построение на доске). Провести биссектрису AD (с помощью транспортира).
Вопрос: какие еще равные элементы вы замечаете в этом треугольнике? Формулируется теорема: В равнобедренном треугольнике углы при основании равны (первое свойство равнобедренного треугольника). Доказательство обсуждается по рисунку на доске. Вопросы учителя: - Какие треугольники мы видим на рисунке? - Какие равные элементы можно выделить в этих треугольниках? - Что можно сказать об элементах равных треугольников? Затем учитель предлагает учащимся записать доказательство в тетрадь. В доказательстве этой теоремы скрыто еще одно свойство равнобедренного треугольника: мы доказали равенство треугольников ABD и ACD, но не назвали соответствующие равные элементы. Какие же элементы остались неназванными? BD = DC и ﮮADB = ﮮ ADC. Делаем вывод: AD – медиана и высота. Учитель еще раз формулирует второе свойство равнобедренного треугольника и просит учащихся отметить, на какие слова в формулировке следует обратить внимание? В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой (биссектриса проводится к основанию, две другие биссектрисы таким свойством не обладают). Треугольник, у которого все стороны равны, называется равносторонним. Людей с давних времен волновал вопрос, подчиняются ли такие неуловимые вещи как красота и гармония, каким- либо математическим расчетам. Можно ли «проверить алгеброй гармонию?»- как сказал А.С.Пушкин. Конечно, все законы красоты невозможно вместить в несколько формул, но, изучая математику, мы можем открыть некоторые слагаемые прекрасного. Одним из символов прекрасного в геометрии, является равносторонний треугольник. У него все стороны и все углы равны, поэтому его еще и называют правильным треугольником. Докажите, что у равностороннего треугольника все углы равны. Работа в парах. ХОД УРОКА Организационный момент. Мотивация урока. Девизом нашего урока является высказывание: “Есть в математике нечто, вызывающее человеческий восторг”, так как на уроках геометрии очень важно уметь, смотреть и видеть, замечать и отмечать различные особенности геометрических фигур. Даю “установку”: Развивать и тренировать свое геометрическое зрение. Кто ничего не замечает, Тот ничего не изучает. Кто ничего не изучает, Тот вечно хнычет и скучает. Изучение нового материала. Работа с учебником.
Физминутка для глаз. -Не поворачивая головы, обведите взглядом стену класса по периметру по часовой стрелке, классную доску по периметру против часовой стрелки, треугольник, изображенный на стенде по часовой стрелке и равный ему треугольник против часовой стрелки. Поверните голову налево и посмотрите на линию горизонта, а теперь на кончик своего носа. Закройте глаза, сосчитайте до 5, откройте глаза и … Мы ладонь к глазам приставим, Итоги урока. Д/з. 1. С каким признаком вы сегодня познакомились? Сформулируйте его. 2. Какие трудности возникли при решении задач? Выучить п. 14. Вопросы с. 112. Решить № 424 (б), 428 (б), 437.
ХОД УРОКА Организационный момент. Мотивация урока. Сегодня мы продолжим путешествие по прекрасной стране Геометрия. Лучше разглядим ее красоту и совершенство. Девизом нашего урока будет: «С любовью к ее величеству - науке геометрии». Пройдемся по ее памятным местам - определениям и теоремам. В геометрии очень много разных тропинок, но главная из них та, которая начинается за школьной партой и учебной книгой. Мы с вами уже побывали на тропинке решения задач и доказательства теорем. Сегодня вновь вернемся к тропинке решения задач и побываем на тропинке красоты чисел. Шагая по тропинкам, погрузимся в мир треугольников. В геометрию тропинки одолеем без запинки. При этом наши суждения должны отличаться строгостью, обоснованностью, краткостью и полнотой, последовательностью и завершенностью, так же не будем пренебрегать интуицией, догадкой, фантазией. Итак, в добрый путь! Изучение нового материала Мы все знаем, что стороны у прямоугольных треугольников имеют свои названия. Начертите любой прямоугольный треугольник в тетрадь и подпишите стороны. Дайте определение сторон треугольника … - гипотенуза – … (напротив прямого угла, перевод с греческого – стягивающая), катет - …(образуют угол …)
Работа с учебником по группам. Изучить и продемонстрировать признаки равенства прямоугольных треугольников. Решить № 442, 443, 444 устно. Историческая пауза. Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал еще в глубокой древности, т. к. эта фигура всегда имела широкое применение в практической жизни. Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней Греции и Древнего Египта. Еще в древности стали вводить некоторые знаки обозначения для геометрических фигур. Древнегреческий ученый Герон (I век) впервые применил знак Прямоугольный треугольник занимал почетное место в Вавилонской геометрии. Стороны прямоугольного треугольника: гипотенуза и катеты. Термин «гипотенуза» происходит от греческого слова «ипонейноуза», обозначающее «тянущаяся над чем-либо», «стягивающая». Слово берет начало от образа древнегреческих арф, на которых струны натягиваются на концах двух взаимно-перпендикулярных подставок. Термин «катет» происходит от греческого слова «катетос», которое означает начало «отвес», «перпендикуляр». Евклид говорил: «Катеты – это стороны, заключающие прямой угол». В Древней Греции уже был известен способ построения прямоугольного треугольника на местности. Для этого использовали веревку, на которой были завязаны 13 узелков, на одинаковом расстоянии друг от друга. При строительстве пирамид в Египте именно так изготавливали прямоугольные треугольники. Наверно поэтому прямоугольный треугольник со сторонами 3,4,5 и назвали египетским треугольником. Самостоятельная работа. Доказать, что против угла 30°в прямоугольном треугольнике лежит катет, равный половине гипотенузы. Работа в парах по учебнику. ХОД УРОКА Организационный момент. Мотивация урока. Изучение нового материала. Решить задачу. Построить треугольник АВС со сторонами 4см, 5см,6см. Учащиеся говорят учителю, что нужно делать, учитель строит. -Как можно с помощью циркуля и линейки построить треугольник? -Может кто-то вспомнит, как мы это делали в 6 классе.
А теперь сами в тетрадях постройте треугольник со сторонами 5см, 3см, 2см. В ходе решения этой задачи учащиеся должны прийти к тому,что не всегда можно построить треугольник. Возникает вопрос: -А всегда ли существует треугольник? Оказывается, что треугольник существует не всегда. -А когда же он существует? Сегодня мы и решим эту проблему. Итак, сейчас мы докажем теорему о существовании треугольника. Она называется теоремой о неравенстве треугольника. Теорема: Каждая сторона треугольника меньше суммы двух других сторон. -Что нам дано? (строим треугольник АВС) -Что нам нужно доказать? На доске и в тетрадях.
Доказать: АВ<АС+СВ
A C
Доказательство. Для доказательства теоремы предлагаю сделать дополнительные построения: 1) продолжить сторону АС, 2) на продолжении отложить отрезок СД, равный стороне СВ.
-Что вы видите на рисунке? -Какие выводы можно сделать? -Давайте, сравним <2 и <АВД.
-Из каких отрезков состоит отрезок АД? Значит, АВ<АС+СД АВ<АС+ВС
Значит, мы доказали теорему о существовании треугольника. -Может кто-то сам попробует доказать эту теорему? -А какие еще неравенства можно записать для треугольника АВС. Работа с учебником. Рассмотреть следствия из теоремы. -Итак, опять вернемся к нашим первым задачам и проверим, существует ли треугольник. а) Треугольник АВС со сторонами 4см, 5см, 6см. 4 < 5+6, 5 < 4+6, 6 < 4+5 (да) б) Треугольник АВС со сторонами 5см,3см,2см. 5 < 3+2 (нет) 2. А теперь проверьте можно ли построить треугольник со сторонами 5см, 6см, 7см (да); 8см, 4см, 3см (нет). Физкультминутка Что такое физкультура? Тренировка и игра. Что такое физкультура? Физ и куль и ту и ра! Руки вверх, руки вниз – это физ. Крутим шею, словно руль – это куль. Ловко прыгай в высоту – это ту. Бегай пол часа с утра – это Ра. Занимаясь этим делом, Станешь сильным, ловким, смелым. Плюс – хорошая фигура. Вот что значит физкультура! На четыре - руки шире, Пять – руками помахать. Шесть – за парту тихо сесть. Самостоятельная работа. Работа в парах. Решить № 477(1, 2), Итоги урока. Д/з. Итак, мы сегодня с вами познакомились с теоремой существования треугольника – «неравенством треугольника». Научились применять её при решении задач. Выучить п. 16, вопросы с.124, решить № 477(3), 478(1) – на 7 баллов, № 2, 4 варианта 4 с. 127 – на 11 баллов.
Организация класса. Мотивация урока. Самостоятельная работа. Решить вариант 1, 2 (№ 2, 3, 4) с.127. Ход урока Организационный момент. Мотивация урока. Контрольная работа 4. Итоги урока. Повторить п. 9-16.
Тема: Треугольник и его элементы. ЦЕЛИ: 1. Изучить понятие треугольника и его элементов в ходе практической работы; 2. Развитие логического мышления учащихся. Формирование устойчивого познавательного интереса к изучению геометрии. 3. Воспитание отношений взаимопомощи и сотрудничества между учащимися в процессе познавательной деятельности; развитие их самостоятельности и творчества. ХОД УРОКА Организационный момент. Мотивация урока. Кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? (Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида). А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного. Зовётся он треугольник, И с ним хлопот не оберётся школьник!
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.061 с.) |





 АС.
АС. АВК =
АВК = 

 Доказательство:
Доказательство:






 =…
=…
 2.Найдите
2.Найдите  =…..,
=….., 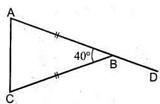 3.Найдите
3.Найдите 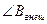 =…
=…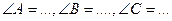
 Выучить п.10. Решить № 297 (б), 298, 300.ть п.рока. Д/з.абота.риала.
Выучить п.10. Решить № 297 (б), 298, 300.ть п.рока. Д/з.абота.риала.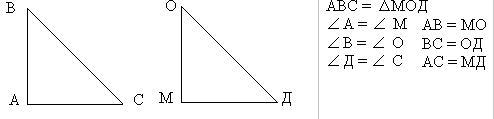







 вместо слова треугольник.
вместо слова треугольник. 4 5
4 5 B Дано: АВС
B Дано: АВС -Как вы думаете, что напрашивается?
-Как вы думаете, что напрашивается? -Какая из сторон меньше? Почему?
-Какая из сторон меньше? Почему?


