
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Итоги урока. Рефлексия. Д/з.Содержание книги Поиск на нашем сайте
Что больше всего тебе запомнилось на уроке? Что удивило? Что понравились больше всего? Каким ты хочешь увидеть следующий урок? Выучить п. 15, вопросы с..118. решить № 446, 448 – на 8 баллов, 460 –на 11баллов. Подготовить сообщение по теме «Египетский треугольник».
Тема: Неравенство треугольника. Цели урока:
Мудр не тот, кто знает много, а тот, чьи знания полезны. Эсхил ХОД УРОКА Организационный момент. Мотивация урока. Актуализация опорных знаний. Теоретический опрос можно провести письменно. Математический диктант (учитель зачитывает начало задания, дети записывают только продолжение – ответы) 1) Периметр треугольника - это… 2) Против меньшей стороны лежит … 3) Сумма углов треугольника … 4) Против большего угла лежит … 5) В прямоугольном треугольнике гипотенуза … 6) Если два угла треугольника равны, то он … 7) Найти все внутренние углы и внешний угол треугольника.
< B = 350 А С
Проверка. Учитель зачитывает задания, один ученик – ответы. Изучение нового материала. Решить задачу. Построить треугольник АВС со сторонами 4см, 5см,6см. Учащиеся говорят учителю, что нужно делать, учитель строит. -Как можно с помощью циркуля и линейки построить треугольник? -Может кто-то вспомнит, как мы это делали в 6 классе.
А теперь сами в тетрадях постройте треугольник со сторонами 5см, 3см, 2см. В ходе решения этой задачи учащиеся должны прийти к тому,что не всегда можно построить треугольник. Возникает вопрос: -А всегда ли существует треугольник? Оказывается, что треугольник существует не всегда. -А когда же он существует? Сегодня мы и решим эту проблему. Итак, сейчас мы докажем теорему о существовании треугольника. Она называется теоремой о неравенстве треугольника. Теорема: Каждая сторона треугольника меньше суммы двух других сторон. -Что нам дано? (строим треугольник АВС) -Что нам нужно доказать? На доске и в тетрадях.
Доказать: АВ<АС+СВ
A C
Доказательство. Для доказательства теоремы предлагаю сделать дополнительные построения: 1) продолжить сторону АС, 2) на продолжении отложить отрезок СД, равный стороне СВ.
-Что вы видите на рисунке? -Какие выводы можно сделать? -Давайте, сравним <2 и <АВД.
-Из каких отрезков состоит отрезок АД? Значит, АВ<АС+СД АВ<АС+ВС
Значит, мы доказали теорему о существовании треугольника. -Может кто-то сам попробует доказать эту теорему? -А какие еще неравенства можно записать для треугольника АВС. Работа с учебником. Рассмотреть следствия из теоремы. -Итак, опять вернемся к нашим первым задачам и проверим, существует ли треугольник. а) Треугольник АВС со сторонами 4см, 5см, 6см. 4 < 5+6, 5 < 4+6, 6 < 4+5 (да) б) Треугольник АВС со сторонами 5см,3см,2см. 5 < 3+2 (нет) 2. А теперь проверьте можно ли построить треугольник со сторонами 5см, 6см, 7см (да); 8см, 4см, 3см (нет). Закрепление изученного материала.
-Известна ли длина треугольника?
-Какие значения может принимать длина основания? - Существует ли равнобедренный треугольник с боковой стороной 2см и основанием 8см? Почему? - Существует ли равнобедренный треугольник с боковой стороной 8см и основанием 2см? Объяснить. Решение. Возможны два случая: 1) АВ=ВС=2см, АС=8см. АС <АВ+ВС,8<2+2, нет. 2) АВ=ВС=8см,АС=2см. 8<8+2, да. Ответ: 8см, 8см, 2см. Решение задач на готовых чертежах.
Решить № 474 (1, 5) устно, 478 (2). Решить вариант 2(№2, 3, 4) с.127. Физкультминутка Что такое физкультура? Тренировка и игра. Что такое физкультура? Физ и куль и ту и ра! Руки вверх, руки вниз – это физ. Крутим шею, словно руль – это куль. Ловко прыгай в высоту – это ту. Бегай пол часа с утра – это Ра. Занимаясь этим делом, Станешь сильным, ловким, смелым. Плюс – хорошая фигура. Вот что значит физкультура! На четыре - руки шире, Пять – руками помахать. Шесть – за парту тихо сесть. Самостоятельная работа. Работа в парах. Решить № 477(1, 2), Итоги урока. Д/з. Итак, мы сегодня с вами познакомились с теоремой существования треугольника – «неравенством треугольника». Научились применять её при решении задач. Выучить п. 16, вопросы с.124, решить № 477(3), 478(1) – на 7 баллов, № 2, 4 варианта 4 с. 127 – на 11 баллов.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.211.58 (0.007 с.) |

 В
В 4 5
4 5 B Дано: АВС
B Дано: АВС -Как вы думаете, что напрашивается?
-Как вы думаете, что напрашивается? -Какая из сторон меньше? Почему?
-Какая из сторон меньше? Почему?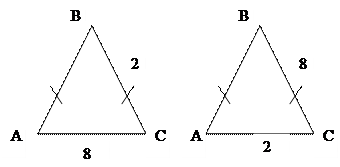 -А длина боковой стороны?
-А длина боковой стороны?



