
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III. Изучение нового материала.Содержание книги
Поиск на нашем сайте 1. Разобрать решение задачи на с. 185 учебника. 2. Правило: Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца. 3. Решить задачу № 1097 (а; в; д). а) 8 – 2 = 6; в) 6 – (-1) = 6 + 1 =7; д) 3,2 – (–4,7) = 3,2 + 4,7 = 7,9. IV. Повторение ранее изученного материала. 1. Решить задачу № 1107 (2) самостоятельно. 2. Решить № 1103. V. Итог урока. 1. Ответить на вопросы на с. 185 учебника. 2. Найти расстояние между точками: а) А (–5,2) и В (–1,8); б) С 3. Решить уравнение: а) 2,4 + х = –2,8; б) 18,24 – у = 20. Домашнее задание: выучить правила п. 34; решить № 1109 (ж – к), 1111, 1113 (в; г), 1115. Прочитать исторический материал на с. 190. Урок 3 Цели: закрепить изученный материал, вырабатывать навыки сложения чисел; проверить степень усвоения учащимися материала; подготовиться к контрольной работе. Ход урока I. Устная работа. 1. Решить устно № 1098 (в; д; е) и 1104. 2. Решить уравнения № 1103 (д; е) на доске. 3. Двое учащихся работают у доски: 1) один ученик решает задачу № 1106; 2) второй ученик решает задачу № 1115. II. Выполнение упражнений. 1. Решить № 1090 (г; д; е) устно. 2. Решить № 1095 с комментированием на месте. 3. Решить № 1092 (д; г; е) на доске и в тетрадях. Решение. г)
Ответ: Ответ: Ответ: 4. Решить № 1089 (устно). 5. Решить задачу № 1097 (г; е) на доске и в тетрадях, № 1097 (б) – самостоятельно. 6. Решить № 1096 (ж; и) самостоятельно, № 1096 (к; л; м) – на доске и в тетрадях. Решение. ж) и) к) л) м)
III. Самостоятельная работа. Вариант I. 1. Выполните вычитание: а)7,5 – (–3,7); в) б) –2,3 – 6,2; г) 2. Решите уравнение: а)7,8 – х = 9,3; б) у – (–17,85) = 12; в) 3. Найдите расстояние между точками: а) С (–6,1) и Д (3,4); б) Е 4. Решите уравнение | х – 2| = 4. 5. Дополнительно: решить № 1108 (1). Вариант II. 1. Выполните вычитание: а) –25,7 – 4,6; в) б) 6,3 – (–8,1); г) 2. Решите уравнение: а) х – (–2,7) = 3,8; б) 16,37 + у = –30; в) 3. Найдите расстояние между точками: а) Е (–8,2) и F (6,6); б) М 4. Решите уравнение | х – 3| = 6. 5. Дополнительно: решить № 1108 (2). Домашнее задание: подготовиться к контрольной работе, выучить правила п. 31–34; решить № 1109 (л – р), № 1112, 1113 (д; е), 1110. Контрольная работа № 10 (1 час) Цели: проверить знания, умения и навыки учащихся по изученному материалу; узнать степень усвоения ими сложения и вычитания положительных и отрицательных чисел. Ход урока I. Организация учащихся на выполнение работы. II. Выполнение работы по вариантам. Вариант I. 1. Выполните действия: а) –3,8 – 5,7; в) 3,9 – 8,4; д) б) –8,4 + 3,7; г) –2,9 + 7,3; е) 2. Найдите значение выражения:
3. Решите уравнение: а) х + 3,12 = –5,43; б) 4. Найдите расстояние между точками А (–2,8) и В (3,7) на координатной прямой. 5. Напишите все целые значения п, если 4 < | п | < 7. Вариант II. 1. Выполните действия: а) –3,5 + 8,1; в) –7,5 + 2,8; д) б) –2,9 – 3,6; г) 4,5 – 8,3; е) 2. Найдите значение выражения:
3. Решите уравнение: а) 5,23 + х = –7,24; б) 4. Найдите расстояние между точками С (–4,7) и Д (–0,8) на координатной прямой. 5. Напишите все целые значения у, если 2 < | у | < 7. Вариант III. 1. Выполните действия: а) –7,5 + 4,2; в) –4,7 + 2,9; д) б) –3,7 – 5,8; г) 3,7 – 5,6; е) 2. Найдите значение выражения:
3. Решите уравнение: а) 4,31 – х = 5,18; б) 4. Найдите расстояние между точками М (–7,1) и N (4,2) на координатной прямой. 5. Напишите все целые значения m, если 4 < | m | < 8. Вариант IV. 1. Выполните действия: а) –7,4 – 2,9; в) 8,7 – 9,4; д) б) –4,1 + 2,8; г) –3,7 + 5,6; е) 2. Найдите значение выражения:
3. Решите уравнение: а) х – 3,22 = –8,19; б) 4. Найдите расстояние между точками К (–0,2) и Р (–3,1) на координатной прямой. 5. Напишите все целые значения z, если 5 < | z | < 9. Домашнее задание: повторить изученный материал. УМНОЖЕНИЕ Урок 1 Цели: ввести правило умножения положительных и отрицательных чисел и научить применять это правило при выполнении упражнений; развивать логическое мышление учащихся. Ход урока I. Анализ контрольной работы. 1. Сообщить результаты контрольной работы и указать ошибки учащихся. 2. Выполнить задания, вызвавшие затруднения у учащихся. II. Устная работа. 1. Решить устно № 1134 (а) и 1135. 2. Решить устно № 1137. Привести свои примеры. III. Объяснение нового материала. 1. Разобрать решение задачи 1 на странице 190 учебника. 0,4 · 200 = 80 (м2). Расход ткани изменился на 80 м2. 2. Разобрать решение задачи 2 (с. 190–191). Вывод: расход ткани на костюмы за день изменился на –80 м2. Значит, –0,4 · 200 = – (0,4 · 200) = –80. Считают, что и 200 · (–0,4) = – (200 · 0,4) = –80. 3. Правило умножения двух чисел с разными знаками. Примеры. –2 · 6 = – (2 · 6) = –12; –6 · 2 = – (6 · 2) = –12; –1,5 · 0,3 = – (1,5 · 0,3) = –0,45; 7,8 · (–0,1) = – (7,8 · 0,1) = –0,78. 4. Вывод: при изменении знака любого множителя знак произведения меняется, а его модуль остается тем же. 5. Если же меняются знаки обоих множителей, то произведение меняет знак дважды и в результате знак произведения не меняется: 8 · 1,1 = 8,8; –8 · 1,1 = –8,8; (–8) · (–1,1) = – (–8,8) = 8,8. Видим, что произведение отрицательных чисел есть число положительное. 6. Правило умножения двух отрицательных чисел. Примеры. –7,5 · (–0,2) = 1,50 = 1,5; –19 · (–0,3) = 5,7; –5,8 · (–6) = 34,8. IV. Закрепление изученного материала. 1. Решить № 1118 и 1119 устно. 2. Решить № 1121 (а; б; в; г; е; ж; з; и; м) устно, № 1121 (д; к; л; н; о) – на доске и в тетрадях. 3. Решить № 1123 (а; б; в) на доске и в тетрадях. Решение. а) 4. Решить № 1129 (а; б) самостоятельно, № 1129 (в; г) – на доске и в тетрадях. Решение. а) б) в) г) 5. Самостоятельно решить № 1140 (а; б). V. Итог урока. 1. Повторить правила, привести свои примеры. 2. Выполнить умножение: а) 64 · (–10); б) –2,8 · 3; в) –4,7 · (–5); г) 6,9 · (–0,1); д) Домашнее задание: выучить правила п. 35; решить № 1143 (а – г), № 1144 (а; б; в), № 1148. Урок 2 Цели: способствовать выработке навыков умножения чисел с разными знаками и умножения отрицательных чисел; закрепить правила умножения десятичных и обыкновенных дробей. Ход урока I. Устная работа. 1. Повторить правила умножения чисел с разными знаками и умножения отрицательных чисел. Привести свои примеры. 2. Проверить по тетрадям выполнение учащимися домашнего задания. 3. Решить № 1134 (б) и № 1138 устно. II. Выполнение упражнений. 1. Решить задачу № 1120, используя рисунок 89 учебника. 2. Решить устно № 1124. 3. Решить № 1121 (п; р; с; т) на доске и в тетрадях. 4. Решить № 1128 (а; б) устно. Учащиеся формулируют правила умножения чисел. 5. Решить № 1123 (г; д; е) на доске и в тетрадях. Решение. г) е) 6. Решить № 1126 на доске и в тетрадях. 7. Объяснить решение № 1127 (а). Решение. а) х + 4 + х + 4 + х + 4 = 3 х + 12 = 3 · 9,1 + 12 = 27,3 + 12 = 39,3. 8. Решить № 1129 (д) на доске; № 1129 (ж) самостоятельно. Решение. д)
ж) 9. Решить № 1130 (а; б) на доске и в тетрадях. Решение. а) б) 10. Повторение материала: 1) Решить задачу № 1141 (а; б). 2) Решить уравнения № 1140 (в; г) самостоятельно с проверкой. III. Итог урока. 1. Повторить правила умножения чисел. 2. Решить № 1128 (в; г) устно. 3. Решить № 1125 письменно и сделать вывод. Домашнее задание: выучить правила п. 35; решить № 1143 (д – з), № 1144 (г; д; е), № 1145 (а – в), № 1147. Урок 3 Цели: обобщить и закрепить изученный материал в ходе выполнения упражнений; проверить знания и умения учащихся; развивать навыки самостоятельной работы. Ход урока
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

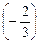 и Д
и Д  .
.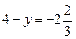 д)
д)  е)
е) 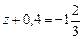
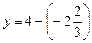
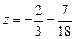
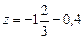

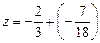
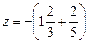
 .
. 
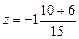
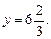
 .
. 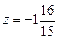
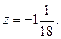
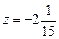 .
.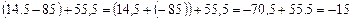 ;
;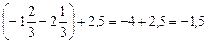 ;
;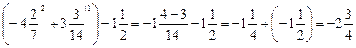 ;
; ;
;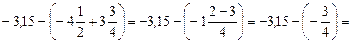
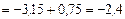 .
.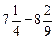 ;
; .
.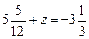 .
.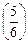 и F
и F  .
. ;
;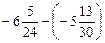 .
.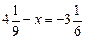 .
.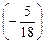 и N
и N 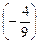 .
.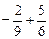 ;
;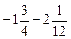 .
. .
.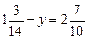 .
. ;
;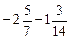 .
.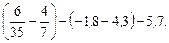
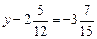 .
.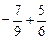 ;
; .
.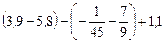 .
.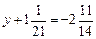 .
.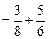 ;
;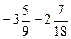 .
. .
.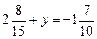 .
.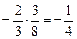 ; б)
; б) 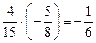 ; в)
; в)  .
. ;
;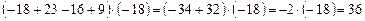 ;
;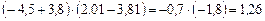 ;
; .
.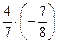 ; е)
; е) 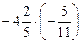 .
. ; д)
; д)  ;
;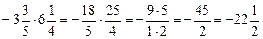 .
.
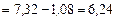 ;
;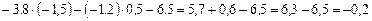 .
.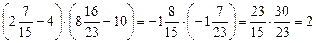 ;
; .
.


