
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III. Закрепление нового материала.Содержание книги
Поиск на нашем сайте
1. Решить № 304 (а; б) на доске и в тетрадях. 2. Решить № 305 с комментированием. 3. Решить задачу № 314 на доске и в тетрадях. Решение. 1) 2)
Ответ: короче шаг сына. 4. Решить задачу № 316. Коллективно учащиеся разбирают решение задачи, а затем самостоятельно записывают решение в тетрадях. Решение. 1) 2)
Ответ: длиннее часть трехметрового бревна. 5. Решить № 319 (а; б; ж; з) и № 321 (а; г) на доске и в тетрадях. 6. Решить № 321 (б; в) с комментированием. 7. Решить № 312 (объясняет учитель). 8. Повторение материала: 1) Решить № 352 (а). Повторить основное свойство дроби и признаки делимости чисел на 2, на 5, на 3, на 9. 2) Решить задачу № 356 (1). Решение. 1) 600 · 0,5 = 300 (км) пролетит первый самолет за 0,5 ч. 2) 750 – 600 = 150 (км/ч) больше скорость второго самолета, чем первого. 3) 300 + 225 = 525 (км) на столько больше километров должен пролететь второй самолет. 4) 525: 150 = 3,5 (ч) через столько часов второй самолет после своего вылета будет впереди на 225 км. Ответ: через 3,5 ч. IV. Итог урока. 1. Выучить правила из пункта 11. 2. Прочитать на странице 50 учебника текст «Говорите правильно». Домашнее задание: изучить п. 11; решить № 359 (а; б; в), № 360 (а; д), № 361, № 373 (в). Урок 2 Цели: упражнять учащихся в сравнении дробей, сложении и вычитании дробей с разными знаменателями; развивать логическое мышление учащихся. Ход урока I. Устная работа. 1. Проверить выборочно номера домашнего задания. 2. Решить № 346 (в) и № 351 (б). II. Выполнение упражнений. 1. Решить № 304 (в; г) с комментированием. 2. Решить № 306 с комментированием. 3. Решить № 307 (а) на доске и в тетрадях. 4. Решить № 313 (самостоятельно). 5. Решить № 319 (в; г; д; k). Четверо учеников самостоятельно решают на доске, остальные в тетрадях, а потом проверяют решение. 6. Решить № 322 (а; в) на доске и в тетрадях. Решение.
7. Решить задачу № 344 (решение объясняет учитель). Решение. Все поле составляет 1. 1) 1: 6 = 2) 1: 4 = 3) Ответ: 8. Выполнить задание № 318 на координатном луче. 9. Самостоятельно решить № 356 (2). Решение. 1) 60 · 0,5 = 30 (км) проедет автобус за 0,5 ч. 2) 75 – 60 = 15 (км/ч) больше скорость легковой машины. 3) 30 + 45 = 75 (км) больше должна проехать легковая машина. 4) 75: 15 = 5 (ч) через столько часов после своего выезда легковая машина будет впереди автобуса на 45 км. Ответ: 5 ч. 10. Решить № 352 с комментированием. Повторить признаки делимости на 10, на 2, на 3. Решение.
III. Итог урока. 1. Повторить правило сравнения дробей. 2. Решить задачи: а) Длина первой доски б) Оля уложила в ящик 15 кг яблок за 8 мин, Катя – 20 кг яблок за 11 мин. Кто из них работал быстрее? Условия этих задач заранее записаны на доске; учитель привлекает к решению этих задач многих учащихся, выясняя степень усвоения ими материала, а решения задач учитель записывает на доске. Домашнее задание: решить № 359 (г; д; е), № 360 (б; е), № 363, № 371. Урок 3 Цели: способствовать развитию навыков сравнения дробей, сложения и вычитания дробей с разными знаменателями; закрепить знание нахождения наименьшего общего кратного чисел. Ход урока I. Устные упражнения. 1. Решить задание № 346 (в; г). 2. Укажите наибольшую дробь: Найдем а) 3. Не приводя дроби к общему знаменателю, определите, какая из них меньше: а) II. Работа по учебнику. 1. Для сложения и вычитания дробей верны изученные ранее свойства этих действий. Они иногда помогают упрощать вычисления. 2. Разобрать решение примеров 4 и 5 на странице 49 учебника. 3. Устные упражнения: найти значение выражения:
III. Выполнение упражнений. 1. Решить № 330 (а), № 331 (а), № 332 (а) на доске и в тетрадях. Решение.
2. Решить № 307 (б) с комментированием. 3. Решить задачу № 317. Решение. НОК (5; 9; 15) = 45.
На решение задачи Юра затратил 4. Решить задачу № 342 самостоятельно. 5. Решить № 322 (б; г) на доске и в тетрадях. Решение.
6. Решить № 319 (е; и) самостоятельно (с проверкой). 7. Решить № 321 (д; е; ж) самостоятельно. 8. Решить № 327 (а; в) на доске и в тетрадях. Решение.
9. Повторение ранее изученного материала. Самостоятельно решить № 348, а затем проверить решение по тетрадям. Решение. а) 0,72 – 0,62 = 0,49 – 0,36 = 0,13; б) 32 – 17,5 = 27 – 17,5 = 9,5; в) 0,52 · 8 = 0,25 · 8 = 2; г) 2,6: 0,13 = 2,6: 0,001 = 260. IV. Итог урока. 1. Повторить правило сравнения дробей. 2. Сравните Домашнее задание: решить № 359 (ж; з), № 360 (в; г; з), № 369 (б), № 364, № 373 (г). Урок 4 Цели: упражнять учащихся в сравнении, сложении и вычитании дробей; научить решать уравнения и задачи; проверить знания и умения учащихся в ходе самостоятельной работы. Ход урока I. Проверка домашнего задания. 1. Двое учащихся работают на доске, решая № 364 и № 369 (б). 2. С остальными учащимися устно решить № 347 (а). 3. Сравните: 4. Назвать дроби в том порядке, как они расположены на координатном луче:
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.233.51 (0.005 с.) |

 (м) составляет шаг папы.
(м) составляет шаг папы. (м) составляет шаг сына.
(м) составляет шаг сына. значит, шаг сына короче.
значит, шаг сына короче. (м) одна седьмая часть трехметрового бревна.
(м) одна седьмая часть трехметрового бревна.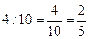 (м) одна десятая часть четырехметрового бревна.
(м) одна десятая часть четырехметрового бревна.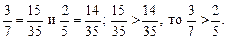

 (часть) убирает за 1 день первый комбайн.
(часть) убирает за 1 день первый комбайн. (часть) убирает за 1 день второй комбайн.
(часть) убирает за 1 день второй комбайн. (часть) уберут за 1 день оба комбайна.
(часть) уберут за 1 день оба комбайна. части.
части. НОК (8; 24; 9) = 72
НОК (8; 24; 9) = 72
 м, а длина второй доски –
м, а длина второй доски –  м. Какая из этих досок длиннее?
м. Какая из этих досок длиннее? НОК (63; 315; 105) = 315.
НОК (63; 315; 105) = 315.



 урока, Нина –
урока, Нина –  урока, а Миша –
урока, а Миша –  урока.
урока.








