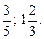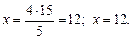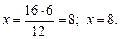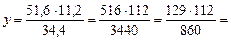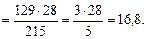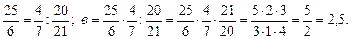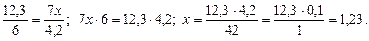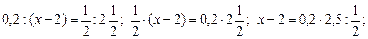Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Проверка изученного материала.Содержание книги
Поиск на нашем сайте 1. Что называется пропорцией? Как называются члены пропорции? 2. Какие из равенств являются пропорциями? а) 2,5: 0,5 = 45: 9; б) 2,5: 0,5 = 3 + 2; в) 0,5 · 12 = 24: 4. 3. Прочитать пропорцию и проверить, верно ли она составлена: а) 9: 3 = 24: 8; б) 1,5: 0,1 = 0,3: 0,2; в) 0,38: 0,01 = 7,6: 0,2. 4. Составить, если можно, пропорции из следующих отношений: а) 2,8: 0,07 и 4: 0,01; б) 500: 125 и 3,2: 0,8; в) 0,3: 0,5 и 0,7: 0,8. 5. Решить устно № 766 (б; в) и № 768 (б; г). II. Объяснение нового материала. 1. Вычислим произведение крайних и произведение средних членов каждой пропорции: а) 20: 5 = 8: 2; 20 · 2 = 40; 5 · 8 = 40; б) 1,2: 0,4 = 30: 10; 1,2 · 10 = 12; 0,4 · 30 = 12. 2. Можно сделать вывод: произведение крайних членов верной пропорции равно произведению средних членов пропорции. Это свойство называют основным свойством пропорции. Для пропорции а: в = с: d оно записывается
3. Чтобы убедиться в том, что пропорция составлена верно, достаточно проверить, равны ли произведения крайних и средних членов. Если эти произведения равны, то пропорция составлена верно. Примеры: 1) Пропорция 0,9: 3,6 = 0,4: 1,6 составлена верно, так как 0,9 · 1,6 = 1,44 и 0,4 · 3,6 = 1,44. 2) Пропорция 5,4: 1,8 = 4: 3 составлена неверно, так как 5,4 · 3 = 16,2; а 1,8 · 4 = 7,2. III. Закрепление изученного материала. 1. Решить № 762 (а; в; д) на доске и в тетрадях. Решение.
Пропорция верная.
Пропорция составлена неверно.
2. Решить № 760 (б) на доске и в тетрадях. 3. Проверить (двумя способами), верно ли равенство: а) 28: 7 = 20: 4; б) 7,5: 1,5 = 120: 24; в) 4,2: 0,3 = 2,8: 0,2. 4. Даны равенства: а) 30 · 3 = 18 · 5; б) 4 · 9 = 0,2 · 180; в) 0,48 · 0,5 = 0,6 · 0,4. Каждое равенство представить в виде пропорции, применяя основное свойство пропорции. Образец: а) 30: 5 = 18: 3 или 18: 30 = 3: 5. 5. Составить, если можно, пропорции из четырех данных чисел: а) 100; 80; 4; 5; б) 5; 10; 9; 4,5; в) 45; 15; 8; 75. 6. Решить № 765 самостоятельно. 7. Повторение ранее изученного материала: а) Решить устно № 771. б) Решить задачу № 773. Решение.
Ответ: IV. Итог урока. 1. Сформулируйте основное свойство пропорции. Привести свои примеры. 2. Верны ли равенства 60: 20 = 18: 6 и 20: 60 = 6: 18? 3. Из следующих равенств составить пропорцию: а) 40 · 30 = 20 · 60; б) 18 · 8 = 9 · 16. Домашнее задание: выучить правила п. 21; решить № 780, 781 (б), № 804, 805. Урок 3 Цели: закрепить знание учащимися основного свойства пропорции; научить применять основное свойство пропорции при решении уравнений; в ходе выполнения упражнений закрепить правила умножения и деления дробей. Ход урока I. Устная работа. 1. Что называется пропорцией? Основное свойство пропорции. Привести свои примеры. 2. Составьте, если можно, пропорции из четырех данных чисел: а) 16; 12; 3; 4; б) 0,7; 0,3; 2; 1; в) 0,15; 0,25; 0,03; 0,05. 3. Проверьте (двумя способами), верно ли равенство: а) 49: 14 = 14: 4; б) 2,5: 0,4 = 3,5: 0,56; в) 0,002: 0,005 = 0,1: 0,25. II. Изучение нового материала в виде беседы. 1. Пропорция 20: 16 = 5: 4 верна, так как 20 · 4 = 16 · 5 = 80. Поменяем местами в этой пропорции средние члены. Получим новую пропорцию: 20: 5 = 16: 4. Она тоже верна, так как при такой перестановке произведение крайних и произведение средних членов не изменилось. Эти произведения не изменяются, если в пропорции 20: 5 = 16: 4 поменять местами крайние члены: 4: 5 = 16: 20. 2. Сделать вывод: если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны. 3. В пропорции можно менять местами правую и левую части, то есть 16: 4 = 20: 5. Любая пропорция может быть записана восемью различными способами. 4. Записать восемью различными способами пропорцию: 10: 5 = 6: 3. Решение. 1) 3: 5 = 6: 10; 2) 10: 6 = 5: 3; 3) 6: 3 = 10: 5; 4) 3: 6 = 5: 10; 5) 5: 10 = 3: 6; 6) 6: 10 = 3: 5; 7) 5: 3 = 10: 6; 8) 10: 5 = 6: 3. 5. Используя основное свойство пропорции, можно найти ее неизвестный член, если все остальные члены известны. Пример 1. Найдите х, если х: 4 = 15: 5. В заданном уравнении неизвестное число х является крайним членом пропорции. Используя основное свойство пропорции, можно записать: х · 5 = 4 · 15. Отсюда находим:
Правило. Неизвестный крайний член пропорции равен произведению средних членов, деленному на известный крайний член пропорции. Пример 2. Решим уравнение 16: х = 12: 6. Неизвестное число х является средним членом пропорции. Используя основное свойство пропорции, можно записать. х · 12 = 16 · 6. Отсюда находим
Правило. Неизвестный средний член пропорции равен произведению крайних членов, деленному на известный средний член пропорции. 6. Работа по учебнику. Разобрать решение примеров 1 и 2 на странице 124 учебника. III. Закрепление изученного материала. 1. Решить № 764 (а; б) самостоятельно. 2. Решить № 763 (а; б; в; д) на доске и в тетрадях. Решение. а) у: 51,6 = 11,2: 34,4;
Ответ: у = 16,8. (Числа 129 и 215 сокращаем на 43). б) в: Ответ: в = 2,5. д) Ответ: х = 1,23. 3. Решить № 763 (з) (объясняет учитель). Решение.
х – 2 = 1; х = 1 + 2 = 3. Ответ: х = 3. 4. Решить задачу на повторение № 775 самостоятельно. IV. Итог урока. Ответить на вопросы к пункту 21 на странице 124 учебника. привести свои примеры. Домашнее задание: ответить на вопросы к п. 21; решить № 777, № 779 (т), № 802. Урок 4 Цели: проверить степень усвоения учащимися изученного материала и знания, умения, навыки в ходе выполнения самостоятельной работы; способствовать развитию логического мышления учащихся. Ход урока
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 925; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

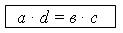
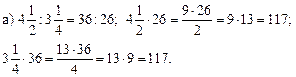
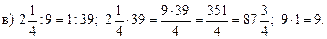
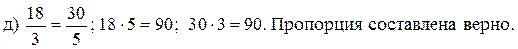
 части составляет угол А от угла В.
части составляет угол А от угла В.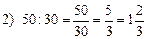 (раза) угол В больше угла А.
(раза) угол В больше угла А.