
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
IV. Закрепление изученного материала.Содержание книги
Поиск на нашем сайте
1. Решить № 1061–1064, используя координатную прямую, заранее начерченную на доске. 2. Решить № 1066 (а; в; д) на доске и в тетрадях, № 1066 (б; г; е; ж) самостоятельно. Решение. а) 26 + (–6) = 20; г) 80 + (–120) = –40; б) –70 + 50 = –20; д) –6,3 + 7,8 = 1,5; в) –17 + 30 = 13; е) –9 + 10,2 = 1,2; ж) 1 + (–0,39) = 0,61. 3. Решить № 1065 самостоятельно. 4. Решить № 1069 (а; б). 5. Повторение ранее изученного материала: а) Решить задачу № 1079 (1) на доске и в тетрадях. Решение. 1) 140 · 3 = 420 (км) – проехали в третий день. 2) 240 + 140 + 420 = 800 (км) – проехали за три дня. 3) 230 · 5 = 1150 (км) – проехали за пять дней. 4) 1150 – 800 = 350 (км) – проехали в пятый день. Ответ: 350 км. б) Решить № 1073 (б). Решение.
Ответ: –9. V. Итог урока. 1. Ответить на вопросы на с. 181 учебника. 2. Выполнить сложение: а) 37 + (–56); в) 4,61 + (–2,29); б) –43 + 75; г) –3,08 + 1,69. Домашнее задание: выучить правила п. 33, решить № 1081 (а – г), № 1083 (а), № 1085. Урок 2 Цели: способствовать выработке навыков сложения отрицательных чисел и сложения чисел с разными знаками; развивать логическое мышление учащихся. Ход урока I. Проверка усвоения материала. 1. Сформулировать правило сложения отрицательных чисел. Решить устно № 1072 (д – ж). 2. Решить устно № 1075 (а) и № 1076 (в; г). 3. Сформулировать правило сложения чисел с разными знаками. 4. Подберите такое число, чтобы получилось верное равенство: а) –4,5 + … = –3,5; г) –7,2 + … = 4,2; б) … + 3 = –2,9; д) … + (–4,9) = –2,9; в) –13,1 + … = –13,1; е) 0,48 + … = 0. II. Выполнение упражнений. 1. Решить № 1066 (з – м) (объясняет учитель). решение. к) л) 2. Выполнить сложение (самостоятельно): а) 3. Решить № 1069 (в; г). 4. Решить № 1067 (а) на доске и в тетрадях, 1067 (б) самостоятельно. Решение. а) (–6 + (–12)) + 20 = –18 + 20 = 2; б) 2,6 + (–1,8 + 5,2) = 2,6 + 3,4 = 6. 5. Решить № 1070 (а; б) на доске и в тетрадях. Решение. а) = –1,35; б)
6. Повторение ранее изученного материала: а) Решить задачу № 1079 (2) самостоятельно. б) Решить № 1080 (1). Решение. 1) 2,35 + 4,65 = 7; 2) 40 – 2,9 = 37,1; 3) 7 · 5,3 = 37,1; 4) 37,1: 37,1 = 1. в) Решить задачу № 1078 (а – г). III. Итог урока. 1. Сформулировать правило сложения отрицательных чисел. Привести свои примеры. 2. Сформулировать правило сложения чисел с разными знаками. Привести свои примеры. 3. Выполните сложение: а) –379 + 948; в) б) –0,81 + 0,66; г) Домашнее задание: выучить правила п. 32 и 33; решить № 1081 (д – л), № 1083 (б; в), № 1084. Урок 3 Цели: способствовать выработке навыков и умений сложения отрицательных чисел и чисел с разными знаками; проверить усвоение материала учащимися в ходе выполнения упражнений. Ход урока I. Устная работа. 1. Повторить правило сложения отрицательных чисел. Привести свои примеры. 2. Повторить правило сложения чисел с разными знаками. Привести свои примеры. 3. Решить устно № 1072 (з; и) и 1073 (а). 4. Решить № 1075 (б; в), записывая решение только на доске. II. Тренировочные упражнения. 1. Решить № 1066 (н – р) на доске и в тетрадях с помощью учителя. Решение. н) о) п) р) 2. Решить № 1067 (в; г) на доске и в тетрадях. Решение. в) (–10 + (–1,3)) + (5 + 8,7) = –11,3 + 13,7 = 13,7 – 11,3 = 2,4; г) (11 + (–6,5)) + (–3,2 + (–6)) = 4,5 + (–9,2) = – (9,2 – 4,5) = –4,7. 3. Решить № 1070 (в; г). Решение. в)
г) 4. Решить № 1068. 5. Повторение ранее изученного материала: Решить задачу № 1078 (д – з) на доске и в тетрадях. III. Самостоятельная работа. Вариант I. 1. Выполните сложение: а) –543 + 458; г) б) 0,54 + (–0,83); д) в) 2. Выполните действия 3. Найдите значение выражения х + 2,6, если х = –1,47;
4. Сколько решений имеет уравнение | х + 2| = –5? Вариант II. 1. Выполните сложение: а) 257 + (–314); б) –0,28 + (–0,18); в) –6 + г) 2. Выполните действия 3. Найдите значение выражения у + (–4,2), если у = 1,83; у = 4. Сколько решений имеет уравнение | у – 9| = –6? Домашнее задание: решить № 1081 (м – р), № 1082, № 1086. ВЫЧИТАНИЕ Урок 3 Цели: способствовать выработке навыков и умений сложения отрицательных чисел и чисел с разными знаками; проверить усвоение материала учащимися в ходе выполнения упражнений. Ход урока I. Устная работа. 1. Повторить правило сложения отрицательных чисел. Привести свои примеры. 2. Повторить правило сложения чисел с разными знаками. Привести свои примеры. 3. Решить устно № 1072 (з; и) и 1073 (а). 4. Решить № 1075 (б; в), записывая решение только на доске. II. Тренировочные упражнения. 1. Решить № 1066 (н – р) на доске и в тетрадях с помощью учителя. Решение. н) о) п) р) 2. Решить № 1067 (в; г) на доске и в тетрадях. Решение. в) (–10 + (–1,3)) + (5 + 8,7) = –11,3 + 13,7 = 13,7 – 11,3 = 2,4; г) (11 + (–6,5)) + (–3,2 + (–6)) = 4,5 + (–9,2) = – (9,2 – 4,5) = –4,7. 3. Решить № 1070 (в; г). Решение. в)
г) 4. Решить № 1068. 5. Повторение ранее изученного материала: Решить задачу № 1078 (д – з) на доске и в тетрадях. III. Самостоятельная работа. Вариант I. 1. Выполните сложение: а) –543 + 458; г) б) 0,54 + (–0,83); д) в) 2. Выполните действия 3. Найдите значение выражения х + 2,6, если х = –1,47;
4. Сколько решений имеет уравнение | х + 2| = –5? Вариант II. 1. Выполните сложение: а) 257 + (–314); б) –0,28 + (–0,18); в) –6 + г) 2. Выполните действия 3. Найдите значение выражения у + (–4,2), если у = 1,83; у = 4. Сколько решений имеет уравнение | у – 9| = –6? Домашнее задание: решить № 1081 (м – р), № 1082, № 1086. Урок 2 Цели: упражнять учащихся в вычитании отрицательных чисел; научить находить длину отрезка на координатной прямой; развивать логическое мышление учащихся. Ход урока I. Устная работа. 1. Повторить правила сложения отрицательных чисел и сложения чисел с разными знаками. Привести примеры. 2. Решить устно № 1098 (а; б; г) и 1101 (в; г). 3. Решить № 1104, записывая на доске приведенные учащимися примеры. 4. Двое учащихся на доске выполняют упражнения из домашнего задания: 1) № 1109 (а – з); 2) № 1116. Решение. 30 % = 0,3. Пусть в альбоме было х российских марок, тогда иностранных марок в альбоме было 0,3 х. Всего в альбоме 1105 марок. х + 0,3 х = 1105 1,3 х = 1105 х = 1105: 1,3 = 11050: 13 = 850 х = 850. В альбоме было 850 российских марок, а иностранных 1105 – 850 = 255 (марок). Ответ: 255 марок, 850 марок. II. Выполнение упражнений. 1. Решить № 1091 (к; л; р; н; п) самостоятельно с проверкой; 1091 (о; с; т) решить на доске и в тетрадях. Решение. к) –7,62 – (–7,62) = –7,62 +7,62 = 0; л) –0,21 – 0 = –0,21 + 0 = –0,21; р) н) п) о) с) т)
2. Решить устно № 1094. 3. Решить № 1092 (а; в) на доске и в тетрадях, 1092 (б) – самостоятельно. Решение. а) –2 + х = 4,3 б) 8,1 + у = –6 в) 5 – х = 1,7 х = 4,3 – (–2) у = –6 – 8,1 х = 5 – 1,7 х = 4,3 + 2 у = –6 + (–8,1) х = 3,3. х = 6,3. у = –14,1. Ответ: х = 6,3. Ответ: у = –14,1. Ответ: х = 3,3. 4. Решить № 1088, используя демонстрационный термометр. 5. Решить № 1096 (а; в; д) на доске и в тетрадях, № 1096 (б; г; е) – самостоятельно. а) (62 – 28) – 40 = 34 – 40 = 34 + (–40) = –6; б) –50 + (37 + 30) = –50 + 67 = 17; в) –6 – (–8 –20) = –6 – (–28) =–6 + 28 = 22; г) –7 –(–12 + 13) = –7 –1 = –7 + (–1) = –8; д) 4,1 – (–1,8 + 2,5) = 4,1 – 0,7 = 3,4; е) (–3,2 + 60) – 0,8 = 56,8 – 0,8 = 56.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.8.179 (0.005 с.) |

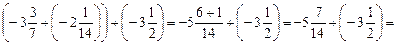
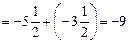 .
. ;
; ; м)
; м) 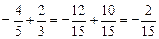 .
.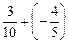 ; б)
; б) 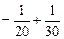 ; в)
; в) 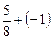 ; г)
; г) 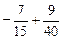 .
.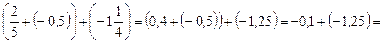
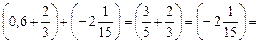
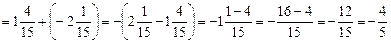 .
. ;
;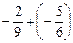 .
. ;
;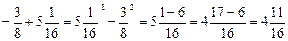 ;
;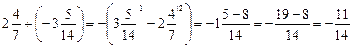 ;
; = 0.
= 0.
 ;
;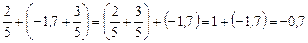 .
.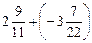 .
.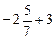 ;
; .
.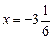 ; х = –18;
; х = –18;  .
.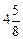 ;
;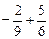 ; д)
; д) 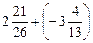 .
.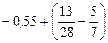 .
.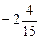 ; у = 16; у =
; у = 16; у = 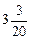 .
. ;
;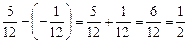 ;
;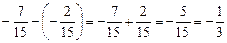 ;
;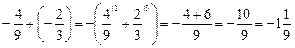 ;
;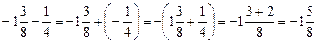 ;
;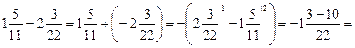
 .
.


