Наибольшее и наименьшее значения функции на ограниченном замкнутом множестве.

Схема исследования функции на экстремум.

_1. z¢_x, z¢_y

_2. Найти критические точки. z¢_x=0, z¢_y=0

_3. Взять производные z¢¢_xx,z¢¢_yy,z¢¢_xy,z¢¢_yx.

_4. C помощью условия существования экстремум сделать вывод.

Теорема Вейерштрасса. Если функция z=f(x,y) непрерывна на замкнутом, ограниченном множестве, то на этом множестве функция принимает наибольшее и наименьшее значение.

 

Правило нахождения максимума и минимума для функции от двух переменных.

1. Найти ОДЗ и обедиться, что оно замкнутое и ограниченное.

2. Исследовать на экстремум, вычислить значение функции.

3. Вычислить значения функции на границах ОДЗ.

4. Из всех значений выбрать наибольшее и наименьшее.

Метод наименьших квадратов.

(рассмотрим для двух величин, остальные аналогично0Пусть (Х,У) – система двух случайных величин. Задача – исследовать связь между Х и У.

М(У/Х=х) – условные математические ожидания случайной величины У при условии, что Х=х (х – фиксированное число) М(У/Х=х)=f(x). Уравнение y=f(x) называется уравнением регрессии СВ У на СВ Ч. Будем приближать функцию y=f(x) к прямой y=kx+b, т.е. попытаемся подобрать k,b так, чтобы y=kx+b как можно лучше апроксимировать функцию y=f(x). В качестве прямой y=kx+b предлагается выбрать ту, на которую лучше всего «ложаться» экспериментальные точки. у₁=kx₁+b Þ Е²₁= (y₁-(kx₁+b))² характеризует степень удалённости точки (х₁,у₁) от прямой y=kx+b Е²₂= (y₂-(kx₂+b))² и т.д. Естественный критерий, характеризующий близость всей совокупности точек к прямой y=kx+b К=åⁿ_i=1E²_i. К=к(к,b) – функция двух переменных. Найдём такие к^*,b^*, которые минимизируют значение К.

К(к,b)= åⁿ_i=1(y_i-(kx_i+b))² Необходимое условие экстремума. DК/Dк=0; DК/Db=0

DК/Dк=åⁿ_i=12(y_i-(kx_i+b))(-х_i)=0

kåⁿ_i=1 х_i²+båⁿ_i=1 х_i =åⁿ_i=1 х_i y_i;

DК/Db=åⁿ_i=12(y_i-(kx_i+b))(-1)=0

åⁿ_i=1 y_i -kåⁿ_i=1 х_i-nb=0.

_í^ì kåⁿ_i=1 х_i²+båⁿ_i=1 х_i =åⁿ_i=1 х_i y_i

î kåⁿ_i=1 х_i+nb=åⁿ_i=1 y_i

cистема двух линейных уравнений с двумя неизвестными к и b.

12. Выпуклые функции в Rⁿ и их свойства.

Отрезок в Rⁿ с концами a, b Î Rⁿ – это множество точек

х (t)= (1-t) a + t b,

где t произвольное число из промежутка [0; 1]. Отрезок с концами a, b обозначается [ a, b ]. Отрезок [ a, b ] совпадает с множеством точек в Rⁿ, представимых в виде с = aа + bb, где a,b - произвольные неотрицательные числа такие, что a+b=1. Множество Р Ì Rⁿ называется выпуклым, если вместе с любыми двумя точками a, bÎР оно содержит и весь отрезок [ a, b ]. Функция n переменных f (х), определенная на выпуклом множестве РÌRⁿ, называется выпуклой, если для любых двух точек a, b Î Р и любых двух чисел a,bÎ[0; 1] таких, что a+b=1, выполняется неравенство

f (aа + bb) ≤ a f (а) + b f (b)

Для непрерывной функции, заданной на выпуклом множестве Р, следующие условия равносильны:

1) f выпукла;

 

 

 

 

Неравенство из пункта 4 называется неравенством Йесена. выпуклая функция наз. строго выпуклой, если неравенство f (aа + bb) ≤ a f (а) + b f (b) строгое при всех a, b из области определения функции и α,β ≥0 таких, что α+β=1.

Функция f наз. (строго) вогнутой, если –f (строго) выпукла, т.е.

f (aа + bb) ≥ a f (а) + b f (b)

Линейная функция f(x)=(c,x)+c₀ одновременно выпукла и вогнута, но не строго.

Свойства выпуклых функций.

1. функция с выпуклой областью определения Р Ì Rⁿ выпукла тогда и только тогда, когда выпукло множество Н_f ={(х,у):хÎР, у≥ f (x)} (из Rⁿ⁺¹) называемое надграфиком функции f (x).

2. Если f (x) выпукла, то функция α f (x) выпукла при α>0 и вогнута при α<0.

3. Если f (x) выпукла на Р, то множество U_f (α)={х: f (x) ≤ α} выпукло при любом α. (обратное утверждение неверно).

4. Сумма любого числа выпуклых функций на множестве Р Ì Rⁿ выпуклана Р, если при этом хотя бы одна из суммируемых функций строго выпукла, то вся сумма строго выпукла.

5. Пусть Р Ì Rⁿ – выпуклое множество, и для каждого i=1,2,…k пусть l _i(x) – линейная функция n переменных, а f_i (t) – функция одной переменной, выпуклая на l _i(Р). Тогда функция F(х)=f₁ (l ₁(x))+…+ f_К (l _К(x)) выпукла на Р. При этом, если все функции f_i (t) строго выпуклы и любая точка однозначно определяется набором (l ₁(а)+…+ l _К(а)), то F(х) строго выпукла.

6. Пусть f выпукла на Р Ì Rⁿ , а φ(t) – возрастающая выпуклая функция на множестве f (Р) ÌR, тогда F(х)= φ(f(x)) выпукла на Р. Если f (x) строго выпукла, то и F(х) строго выпукла.

7. Дифференциируемая функция f (x) выпукла на множестве Р Ì Rⁿ тогда и только тогда, когда (grad f (a), b-a) ≤ f (b)- f (a) для любых a,bÎР

8. Пусть f (x) – функция, непрерывная на отрезке [ a, b ]ÌR и дважды дифференциируемая на (a, b). Для выпуклости функции f (x) на [ a, b ] необходимо и достаточно выполнение неравенства f˝ (x)≥0 для всех tÎ (a, b). Для строгой выпуклости f (x) добавляется условие f˝ (x)≠0 ни на одном интервале, содержащемся в (a, b).

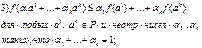
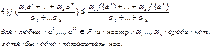
9. Пусть D – выпуклое открытое множество в пространстве Rⁿ, f (x)= f (x₁,…,х_n) – функция, имеющая в D непрерывные частные производные второго порядка. Для каждой точки хÎ D положим