
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие минимизации логических функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При представлении функции алгебры логики (ФАЛ) математическим выражением используют два вида ее представления. Дизъюнктивной нормальной формой (ДНФ) называется логическая сумма элементарных логических произведений, в каждое из которых аргумент или его отрицание входят один раз. ДНФ может быть получена из таблицы истинности следующим образом: для каждого набора аргументов, на котором функция равна «1», записывают элементарные произведения переменных, причем переменные, значение которых равно нулю, записывают с инверсией. Полученные произведения, называемые минтермами, суммируют. Конъюнктивной нормальной формой (КНФ) называется логическое произведение элементарных сумм, в каждую из которых аргумент или его отрицание входят один раз. КНФ может быть получена из таблицы истинности: для каждого набора аргументов, на котором функция равна «0», составляют элементарную сумму, причем переменные, значение которых равно «1», записываются с отрицанием. Полученные суммы объединяют операцией логического умножения.
Пример 1 Таблица 1.2 — Таблица истинности
Задана логическая функция 3-х переменных, которая равна единице в случае, если хотя бы две из входных переменных равны единице. Запишем эту функцию в виде таблицы истинности (табл. 1.2). Для данной логической функции ДНФ имеет вид
ДНФ, полученная суммированием конституента единицы, называется совершенной (СДНФ). Для функции из примера 1 КНФ:
Иногда удобнее пользоваться не самой ФАЛ, а ее инверсией. В этом случае при использовании вышеописанных методик для записи СДНФ надо использовать нулевые, а для записи СКНФ единичные значения функции. Минимизация ФАЛ — сокращение логического выражения функции до минимума. Целью минимизации является минимизация стоимости ее технической реализации. Метод минимизации ФАЛ с использованием карт Вейча (Карно) базируется на табличном виде представления ФАЛ. Картой Вейча (Карно) называется таблица, число клеток которой для функции и переменных равно 2n, причем каждому минтерму соответствует своя клетка карты (рис. 1.15).
Рисунок 1.15 — Вид карты Вейча (Карно) для функции 3 переменных Если требуется представить на карте Вейча (Карно) логическую функцию, заданную в виде ДНФ, в соответствующие клетки заносятся единицы. Остальные клетки остаются незаполненными или заполняются нулями. Логическая функция на карте Вейча (Карно) представляется совокупностью клеток, заполненных единицами, а инверсия функции представляется совокупностью пустых или заполненных нулями клеток. При минимизации ФАЛ используются либо ее единичные, либо нулевые значения. В обоих случаях получаются равносильные выражения, которые, однако, могут отличаться по числу членов и выполненных логических операций.
Основным критерием минимизации ФАЛ является критерий уменьшения количества элементарных логических элементов при использовании только однородных элементов, например, только типа И-НЕ (ИЛИ-НЕ). Алгоритм минимизации сводится к следующему: На карте Вейча выделяют прямоугольные области, объединяющие выбранные значения функции («1» или «0»). Причем каждая область должна содержать 2k клеток, где k может принимать значения 0; 1; 2; 3, т.е. 1; 2; 4; 8 клеток. Выделенные области могут пересекаться, т. е. одна клетка может входить в несколько разных областей. Каждая из выделенных областей является самостоятельным произведением переменных и носит название импликанты. Для каждой выделенной области записывается произведение тех аргументов, которые в соседних клетках не изменяют своего значения. Сумма полученных произведений образует минимальную ДНФ.
Пример 2
Пример 3
объединяем по «1»
Следует также отметить, что, поскольку карты Вейча (Карно) функции 3-х переменных представляют собой объемные фигуры, при формировании областей необходимо помнить, что в одну область объединяются крайние столбцы карты 3-х переменных (рис. 1.15). Рисунок 1.16 — Объединение крайних областей в единую область
Регистр — электронное устройство, предназначенное для кратковременного хранения и преобразования многоразрядных двоичных чисел. Регистр состоит из триггеров, количество которых определяет, сколько разрядов двоичного числа может хранить регистр – разрядность регистра (рис. 1.16, а). Для организации работы триггеров могут быть использованы логические элементы.
Рисунок 1.17 — Регистр а) общее представление, б) условно-графическое обозначение По способу ввода и вывода информации регистры подразделяются на параллельные и последовательные. В последовательном регистре триггеры соединены последовательно, т. е. выходы предыдущего триггера передают информацию на входы последующего. Тактовые входы С триггеров соединены параллельно. Такой регистр имеет один информационный вход и вход управления - тактовый вход С. В параллельном регистре запись в триггеры происходит одновременно, для чего имеется четыре информационных входа. На рисунке 1.17 представлено УГО и назначение выводов четырёхразрядного параллельно-последовательного регистра. Счетчик импульсов — электронное устройство, предназначенное для подсчета числа импульсов, поданных на вход. Количество поступивших импульсов выражается в двоичной системе счисления. Счетчики импульсов являются разновидностью регистров (счетные регистры) и строятся соответственно на триггерах и логических элементах. Основными показателями счетчиков являются коэффициент счета К 2n - число импульсов, которое может быть сосчитано счетчиком. Например, счетчик, состоящий из четырех триггеров, может иметь максимальный коэффициент счёта 24=16. Для четырехтриггерного счетчика минимальный выходной код - 0000, максимальный -1111, а при коэффициенте счёта Кс = 10 выходной счет останавливается при коде 1001 = 9. На рисунке 1.18 представлены УГО четырехразрядного счетчика и временные диаграммы работы. При поступлении первого счетного импульса по его спаду первый триггер переходит в состояние Q1 = 1, т.е. в счетчике записан цифровой код 0001. По окончании второго счетного импульса первый триггер переходит в состояние «0», а второй переключается в состояние «1». В счетчике записывается число 2 с кодом 0010.
Рисунок 1.18 — Двоичный четырехразрядный счетчик а) условно-графическое обозначение, б) временные диаграммы работы Подсчет числа импульсов является наиболее распространенной операцией в устройствах цифровой обработки информации. В процессе работы двоичного счетчика частота следования импульсов на выходе каждого последующего триггера уменьшается вдвое по сравнению с частотой его входных импульсов (рис. 1.18, б). Поэтому счетчики применяют также в качестве делителей частоты.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 897; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.203.104 (0.006 с.) |


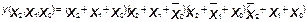

 При объединении клеток с нулевыми значениями ФАЛ получим ФАЛ, инверсную заданной.
При объединении клеток с нулевыми значениями ФАЛ получим ФАЛ, инверсную заданной. ;
;


 ;
; ;
;





