
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие определённого интегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные свойства интеграла. Установим ряд важных свойств определенного интеграла. Большая часть этих свойств присуща интегралам от любых интегрируемых функций, но мы будем формулировать их для функций непрерывных. Теорема 1. Если f (x) и g (x) - две непрерывные функции, заданные на промежутке [ a, b ], то
т. е. интеграл суммы равен сумме интегралов слагаемых. В самом деле, составляя интегральную сумму для функции f (x) + g (x), очевидно, будем иметь
после чего остается перейти к пределу при λ → 0. Аналогично доказывается Теорема 2. Если f (x) - непрерывная функция, а c - постоянное число, то
т. е. постоянный множитель можно выносить за знак интеграла. Теорема 3. Пусть f (x) непрерывна на промежутке [ a, b ]. Если этот промежуток точкой c разложен на части [ a, c ] и [ c, b ], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.
В самом деле, будем при раздроблении промежутка [ a, b ] на части включать c в число точек деления. Если c = xm, то
Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [ a, b ], [ a, c ] и [ c, b ]. Остается перейти к пределу при λ → 0. Доказанную теорему можно высказать в более общей форме. Для этого нам понадобится расширить смысл символа интеграла. Если f (x) - любая функция, определенная в точке a, то по определению полагаем
Таким образом, интеграл с совпадающими пределами равен нулю. Пусть функция f (x) интегрируема на промежутке [ a, b ]. Тогда по определению полагаем
Таким образом, при перестановке пределов интегрирования определенный интеграл меняет знак. Теперь можем привести упомянутую более общую форму теоремы 3: Теорема 4. Пусть функция f (x) непрерывна в промежутке [ A, B ]. Если a, b, c суть точки этого промежутка, то
В самом деле, если из точек a, b и c две (а тем более три) совпадают, то равенство (13) очевидно. Пусть же все эти точки различны. Если a < c < b, то дело сводится к теореме 3. Прочие случаи взаимного расположения точек a, b, c тоже легко свести к той же теореме. Пусть, например, c < b < a. Тогда
откуда
и остается дважды применить формулу (12). Свойство интеграла, выражаемое теоремами 3 и 4, называется аддитивностью его, как функции промежутка интегрирования.
Теорема 5. Если f (x) - непрерывная функция, заданная на промежутке [ a, b ], то существует такая точка
В самом деле, пусть M и m наибольшее и наименьшее значения f (x) на промежутке [ a, b ]. Составим для f (x) какую-нибудь интегральную сумму
Так как при всех k будет m ≤ f (ξk) ≤ M, а xk +1 > xk, то m (xk +1 - xk) ≤ M (xk +1 - xk). Складывая такие неравенства и замечая, что
получим: m (b - a) ≤ σ ≤ M (b - a). Переходя в этом неравенстве к пределу при λ → 0, приходим после деления на b - a к новому неравенству
Таким образом, частное
есть число, лежащее между наибольшим и наименьшим значениями непрерывной функции. Как известно, тогда и само это число должно являться одним из значений той же функции. Поэтому в [ a, b ] обязательно существует такая точка ξ, что h = f (ξ), а это равносильно равенству (14). Заметим, что равенство (14) справедливо не только при a < b, но и при a = b (тогда обе части этого равенства нули), а также и при a > b (этот случай приводится к рассмотренному изменением знаков). В первом из этих случаев будет ξ = a, а во втором a ≥ ξ ≥ b. Теорему 5 обычно называют теоремой о среднем значении. Из нее вытекает ряд свойств интеграла, выражающихся неравенствами. Теорема 6. Если f (x) - неотрицательная непрерывная функция и нижний предел интеграла не больше верхнего*, то и сам интеграл будет числом неотрицательным
Действительно, в этом случае оба сомножителя правой части формулы (14) неотрицательны.
* Если в интеграле Последний результат можно несколько уточнить. Теорема 7. Если a < b, а f (x) - непрерывная неотрицательная функция, которая хотя бы в одной точке [ a, b ] отлична от нуля, то
В самом деле, пусть x 0 (a < x 0 < b) - такая точка, что f (x 0) > 0. Возьмем столь малое δ > 0, чтобы при | x - x 0 | < δ было f (x) > 0, что, очевидно, возможно, благодаря непрерывности нашей функции. Не ограничивая общности, можно принять, что a ≤ x 0 - δ, x 0 + δ ≤ b. Тогда
Первый и третий интегралы правой части по предыдущей теореме неотрицательны, а второй интеграл по теореме о среднем представим в форме
и потому строго положителен. Теорему 7 можно, очевидно, формулировать и так:
Теорема 8. Пусть f (x) - неотрицательная непрерывная функция, заданная в [ a, b ], причем a < b. Если
то f (x) всюду на [ a, b ] равна нулю. В обеих теоремах 7 и 8 (в отличие от теоремы 6) нельзя отбросить условия непрерывности подинтегральной функции. Например, функция, которая в конечном числе точек [ a, b ] равна единице, а в остальных точках этого промежутка равна нулю, будет неотрицательной и нетождественной нулю, а интеграл от нее (как показано в пункте Определенный интеграл) равен нулю. Теорема 9. Если a ≤ b, а f (x) и u · g (x) - две непрерывные функции, которые на [ a, b ] удовлетворяют условию f (x) ≤ g (x), то
т. е. при нормальном порядке пределов интегрирования неравенство можно интегрировать почленно. Действительно,
Если бы мы допустили, что a < b и что хоть в одной точке оказывается f (x) < g (x), то смогли бы и в (15) исключить знак равенства. Теорема 10. Если a ≤ b и f (x) непрерывна на [ a, b ], то
т. е. при нормальном порядке пределов интегрирования абсолютная величина интеграла не превосходит интеграла от абсолютной величины подинтегральной функции. В самом деле, интегрируя неравенств - | f (x) | ≤ f (x) ≤ | f (x) |, находим:
а это равносильно неравенству (16). Из теоремы о среднем значении немедленно вытекает также следующая важная оценка интеграла: Теорема 11. Если непрерывная функция f (x) для всех x между a и b удовлетворяет неравенству | f (x) | ≤ K, то
Отметим, наконец, что поскольку определенный интеграл есть постоянное число, вполне определяемое пределами интегрирования и подинтегральной функцией, то обозначение переменной интегрирования никакого значения иметь не может, так что символы
обозначают одно и то же число. Это небесполезно сопоставить с тем, что у интегралов неопределенных дело обстоит не так. Например,
Поэтому, сводя интеграл
с помощью подстановки sin x = z к интегралу
мы должны иметь в виду, что последний интеграл равен не
Метод решения определенного интеграла от четной функции Рассмотрим определенный интеграл вида Если функция подынтегральная Многие догадались, почему так, тем не менее, рассмотрим конкретный пример с чертежом: Пример 1 Вычислить определенный интеграл В данном случае: Согласно правилу, на симметричном относительно нуля отрезке А сейчас геометрическая интерпретация. Да, продолжаем мучить несчастную параболу…. Любая чётная функция, в частности Определенный интеграл
Аналогичная история происходит с любой чётной функцией Некоторые скажут: «Да зачем это всё нужно, можно ведь и так вычислить определенный интеграл». Можно. Давайте вычислим: Но удобно ли было подставлять отрицательный нижний предел? Не очень-то. Кстати, ненулевой процент студентов допустит ошибку в знаках. Гораздо проще и приятнее подставить ноль. Замечу, что это еще был простой демонстрационный пример, на практике всё бывает хуже. Кроме того, рассматриваемый прием часто применяется при вычислении двойных интегралов, тройных интегралов, где вычислений и так хватает. Короткий разминочный пример для самостоятельного решения:
Вопрос. Определённый интеграл с переменным верхним пределом. Формула Ньютона Лейбница. Примеры.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 718; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.79.100 (0.008 с.) |





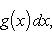










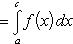
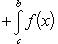









 (11)
(11)

 (12)
(12)


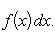 (13)
(13)




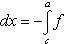



 , что
, что
 (14)
(14)














 будет a ≤ b, то будем говорить, что порядок пределов интегрирования - нормальный.
будет a ≤ b, то будем говорить, что порядок пределов интегрирования - нормальный.


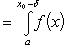



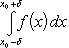

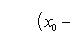






 (15)
(15)






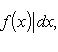 (16)
(16)







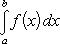

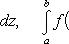

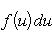






 , а именно,
, а именно,  с тем, чтобы в этом выражении заменить z на sin x.
с тем, чтобы в этом выражении заменить z на sin x.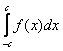 . Легко заметить, что отрезок интегрирования
. Легко заметить, что отрезок интегрирования  симметричен относительно нуля.
симметричен относительно нуля. является чётной, то интеграл
является чётной, то интеграл  .
.
 . Как проверить функцию на чётность? Нужно вместо «икс» подставить
. Как проверить функцию на чётность? Нужно вместо «икс» подставить  .
.
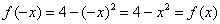 , значит, данная функция является чётной.
, значит, данная функция является чётной. наш интеграл от чётной функции можно вычислить следующим образом:
наш интеграл от чётной функции можно вычислить следующим образом:
 :
:






