Численные характеристики последствий

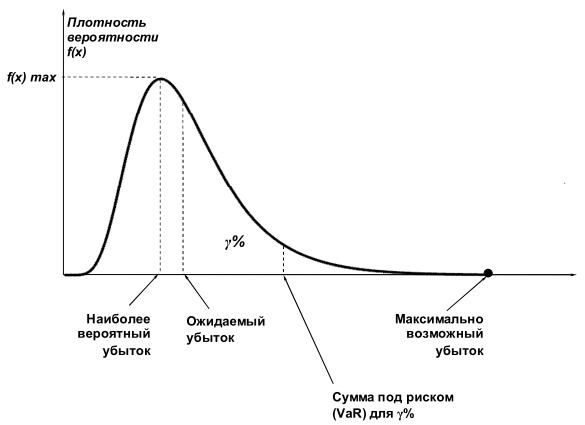
Для упрощения сравнения различных рисков удобно представлять последствия их реализации в виде одного числа. В ситуации, когда последствия детерминированы (фиксированы) это просто. Однако, если они распределены на некотором интервале (иногда бесконечном), то возникает проблема выбора единственного численного значения, с помощью которого можно было бы описать последствия. Практикой выработано несколько вариантов, которые мы рассмотрим на примере выбора численной характеристики последствий экономических рисков (т.е. убытков).

В зависимости от ситуации в качестве меры последствий экономического риска используют несколько показателей (см. Рис.5.3):

1. максимально возможный убыток (maximum possible loss);

2. наиболее вероятный убыток (maximum probable loss);

3. ожидаемый убыток (expected loss);

4. сумма под риском (др. названия - ценность под риском, сумма на риске) (Value-at-Risk, VaR)

 

 

Рис.5.3. Численные характеристики последствий

Максимально возможный убыток представляет собой предельно возможные негативные последствия. Он применяется для описания реального ущерба, связанного с полным уничтожением (утратой) объекта. Но для большинства рисков такая оценка является слишком пессимистичной, поскольку убытки достигают максимального значения относительно редко.

Наиболее вероятный убыток с математической точки зрения соответствует моде распределения случайной величины, описывающий последствия (то есть значения убытка, при котором функция плотности вероятности принимает наибольшее значение).

Ожидаемый убыток соответствует математическому ожиданию. Вероятность отклонения последствий от него как в меньшую, так и в большую сторону одинаковы и равны 50%. Для симметричных распределений (например, для нормального распределения) наиболее вероятный и ожидаемый убытки совпадают. Часто убытки хорошо моделируются случайными величинами, распределение которых имеет правостороннюю асимметрию. В этом случае мода меньше математического ожидания, поэтому наиболее вероятный убыток является более оптимистичной оценкой последствий, чем ожидаемый.

Описанные первые три варианта оценки достаточно широко используются на практике, однако имеют общий существенный недостаток - они не учитывают разброса значений. В ряде случаев это не позволяет корректно сравнить риски.

Пример:

Годовая доходность двух ценных бумаг описывается случайными величинами, распределенными нормально с одинаковыми математическими ожиданиями, но разными среднеквадратическими отклонениями (СКО) (см.Рис.5.4). Наиболее вероятные и ожидаемые результаты инвестирования у них совпадают. Однако ценная бумага с большим СКО представляет для осторожного инвестора больший риск, т.к. вероятность значительных отклонений от ожидаемого значения для нее выше.

Чтобы иметь возможность учитывать степень разброса последствий используют такой показатель, как "сумма под риском". Он показывает размер убытка, который не будет превышен с заданной вероятностью. Математически это можно записать следующим образом:

Р(Х <= VaR) = y

Х - случайная величина;

VaR - искомое значение суммы под риском;

y - заданное значение вероятности, с которой случайная величина Х не должна превысить значение суммы под риском VaR;

Иными словами сумма под риском VaR соответствует квантилю распределения для заданного значения вероятности y.

В последнее время данную характеристику активно применяют для оценки рисков в финансовой деятельности. В рассмотренном выше примере, при одинаковой заданной вероятности сумма под риском для ценной бумаги с большим СКО выше, что подтверждает более высокий уровень риска.

 

 

Рис.5.4. Иллюстрация сравнения двух рисков по показателю "сумма под риском" (VaR)

Рассмотренные подходы к описанию убытков применимы также и для последствий неэкономических рисков, которые имеют численное выражение. Подобным образом могут измеряться потери в натуральной форме, число погибших в результате аварии и т.д.

В последнее время кроме измерения отдельных рисков все чаще предпринимаются попытки найти подходы к оценке суммарного (совокупного) риска фирмы. Однако общепризнанной методики пока не выработано.

Методы измерения риска

Количественная оценка вероятности и последствий (или распределения случайных величин, с помощью которых моделируется рисковая ситуация) может осуществляться разными методами. Выбор того или иного способа зависит, в первую очередь, от объема доступной, в т.ч. статистической, информации о риске и требуемой точности оценок. Также приходится учитывать фактический уровень риска. Чем меньше вероятность наступления, тем труднее измерить риск.

Общий принцип при выборе методов измерения сводится к максимально возможному использованию доступных статистических данных. Если их нет, они недостаточны или неприменимы, фактический материал заменяется теоретическими гипотезами или экспертными оценками.

Всего можно выделить четыре группы методов количественной оценки рисков:

1. Статистические методы.

2. Вероятностно-статистические.

3. Теоретико-вероятностные.

4. Экспертные.

 

Статистические методы

В основе данных методов лежит оценка вероятности наступления случайного события исходя из относительной частоты появлений данного события в серии наблюдений. Данные методы являются наиболее предпочтительными, поскольку, во-первых, они достаточно просты, и, во-вторых, их оценки базируются на фактических данных (а, практика, как известно, является критерием истины).

Но статистические методы не применимы там, где нет достаточного объема наблюдений. Для корректной оценки рисков редких событий требуется очень больший объем статистических данных. Кроме того, сбор и обработка таких массивов информации может оказаться слишком долгой и дорогой.

Пример:

Отдельный узел сложной технической системы разработан уже давно, производится и эксплуатируется достаточно длительный период. За это время накоплено большое число статистических данных, которые позволяют рассчитать частоту отказа данного узла, которая служит несмещенной оценкой вероятности реализации риска отказа.