Дискретные и непрерывные модели

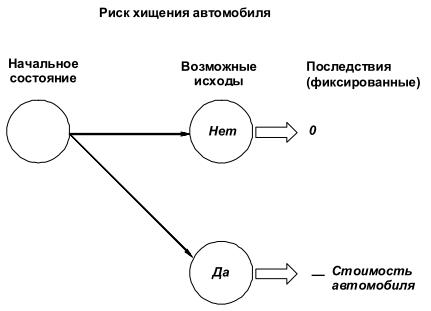
Риск, как и лежащая в его основе неопределенность, подразумевает возможность наступления различных по последствиям исходов, каждый из которых вероятен в большей или меньшей степени. С математической точки зрения это может быть описано (и далее измерено) с использованием случайных величин (СВ). Существуют дискретные и непрерывные случайные величины. Дискретными называют такие СВ, которые могут принимать только конечное или счетное множество значений. Непрерывные СВ могут принимать любые значения из некоторого замкнутого или открытого (в т.ч. бесконечного) интервала.

В самом простом случае, когда существует конечное множество исходов, каждый из которых имеет фиксированные (неслучайные) последствия, риск может быть описан с помощью одной дискретной случайной величины.

Пример:

Риск убытков от хищения автомобиля в течение некоторого периода времени для собственника может быть описан дискретной случайной величиной, имеющей два исхода с фиксированными последствиями (см. Рис.5.1):

1. "хищение не произошло", последствия равны нулю;

2. "хищение произошло", последствия равны стоимости автомобиля.

Для обоих исходов последствия принимают заранее известные неслучайные значения.

 

Рис.5.1. Пример дискретной модели риска хищения автомобиля.

 

 

Рис.5.2. Пример комбинированной дискретно-непрерывной модели риска повреждения автомобиля в ДТП.

 

Когда риск связан с изменением показателя, который может принять любое значение на некотором интервале, можно достаточно просто моделировать риск, описав данный показатель с помощью непрерывной случайной величины, распределенной на указанном интервале.

Пример:

Риск инвестора, купившего акции конкретного эмитента по определенной цене. В будущем возможны отклонения курса этих акций, как в большую, так и в меньшую сторону по отношению к цене покупки. При этом отклонения в меньшую сторону являются неблагоприятными, что и составляет риск инвестора. Он может быть описан с помощью непрерывной случайной величины, характеризующей его потери или выгоду (т.е. последствия) в зависимости от цены акции. Эти последствия могут принимать любые значения в интервале от "минус цена покупки" до "плюс бесконечность". Однако если брать достаточно короткий период прогнозирования, то курс акций, скорее всего, не уйдет далеко от ожидаемого значения, хотя такие отклонения все-таки возможны.

Дискретные или непрерывные модели могут комбинироваться при описании конкретной рисковой ситуации. Например, если в дискретной модели последствия всех или отдельных исходов могут принимать множество значений непредвиденным для субъекта способом, то они должны описываться непрерывной случайной величиной.

Пример:

В результате ДТП автомобиль может получить различные повреждения, убытки от которых могут достичь его стоимости (или даже превысить ее). Однако такие тяжелые последствия маловероятны. Предсказать заранее, какие именно повреждения получит автомобиль и каков будет ущерб, нельзя. Поэтому риск убытков от повреждения автомобиля в дорожно-транспортном происшествии в отдельной поездке может быть описан с помощью двух случайных величин (см. Рис.5.2):

1. дискретной, характеризующей возможность наступления ДТП и имеющей два исхода ("ДТП не произошло" и "ДТП произошло"), и

2. непрерывной, описывающей размер ущерба (последствия) в случае его наступления.

При этом убытки (последствия) от исхода "ДТП не произошло" неслучайны и равны нулю.

В зависимости от особенностей описываемого (моделируемого) риска, целей исследования и требуемой подробности одну и ту же ситуацию неопределенности можно представлять как в виде дискретной, так и в виде непрерывной модели, а также в виде их комбинации.

Пример:

Риск хищения имущества на предприятии в течение года можно количественно описать с использованием:

а) дискретной модели, использующей дискретную случайную величину (СВ), которая может принимать два ("краж не было" - "кража(и) были") или более значений ("краж не было" - "была 1 кража" - "было 2 кражи" и т.д.);

б) непрерывной модели, при которой риск описывается непрерывной СВ "убытки от краж за год";

в) комбинации указанных моделей, сочетающей, например, использование дискретной СВ "количество краж в течение года" и непрерывной СВ "размер убытка от одной кражи".

В любом случае, когда риск описывается с использованием случайных величин (дискретных или непрерывных), необходимо знать их распределение (его вид и значения параметров распределения) или хотя бы численные характеристики этих величин (прежде всего, математическое ожидание, дисперсию или среднеквадратическое отклонение). Тогда можно говорить о том, что риск измерен (количественно оценен). В результате изучения различных случайных процессов для некоторых случайных величин, используемых при моделировании рисков, подобраны наиболее удачно описывающие их виды распределения.

Полная информация о распределении описывающей риск случайной величины, безусловно, очень полезна. Однако для простого сравнения рисков часто достаточно знать только две характеристики: математическое ожидание и численную характеристику разброса значений относительно него (дисперсию или среднеквадратическое отклонение (СКО)).