Цифровые модели поверхностей: TIN.

Нерегулярные триангуляционные сети (Triangulation Irregular Network – TIN) являются альтернативой растровым DEM и используются во многих геоинформационных системах, системах автоматизированного картографирования, пакетах построения контуров. Модели TIN разработаны в 1970-х годах как простой способ построения поверхностей по нерегулярно расположенным точкам.

Модель TIN обладает некоторыми преимуществами перед растровыми DEM. В первую очередь, расположение точек адаптировано к местности: в равнинных участках точки расположены реже, а гористых – чаще. Выборочные точки соединяются прямыми отрезками, образующими треугольники, внутри которых поверхность задается плоскостью. Поверхность непрерывна, треугольники соединены между собой. Структуры данных в TIN-моделях более компактны и экономичны: TIN-модели из сотен точек может соответствовать растровая DEM из десятков тысяч точек. Несмотря не простоту модели, создание TIN требует решения ряда сложных задач: как размещать выборочные точки, как соединять точки в треугольники, как моделировать поверхность внутри треугольника.

Рассмотрим задачу выбора размещения точек триангуляции на следующем примере: имеется растровая DEM или оцифрованные изолинии рельефа, необходимо выбрать точки таким образом, чтобы наиболее точно представить поверхность в TIN-модели.

Рассмотрим алгоритмы выбора точек DEM.

Алгоритм Фаулера – Литтла основан на поиске особых точек поверхности – пиков, хребтов, впадин и т.п. Поверхность проверяется скользящим окном размера 3 x 3. При этом соседи центральной ячейки помечаются плюсом, если их высота больше, и минусом если меньше. Очевидно, точка является пиком, если все восемь ее соседних ячеек помечены минусом. Аналогично, точка является впадиной, если все восемь ее соседних ячеек помечены плюсом. Точка является ущельем или перевалом, если плюсы и минусы вокруг точки образуют хотя бы два полных цикла:

{ + + – – – – + + } = 2 цикла; { + – + – + – + – } = 4 цикла.

Далее слой обрабатывается окном 2 x 2 таким образом, что каждая ячейка по очереди становится во все позиции окна. Точка является гребнем горы, если в каждом из четырех окон она не самая низкая. Аналогично, точка принадлежит протоку, если во всех четырех окнах она не самая высокая. Затем, начиная от ущелий или впадин, ищутся связные протоки, пока не будут достигнуты пики (поиск можно вести и в обратном направлении). В результате получаются соединенные линиями пики, протоки, впадины, ущелья и перевалы. По выбранным точкам создаются треугольники.

 

 

Алгоритм VIP (очень важная точка) в отличие от предыдущего алгоритма, в котором идентифицируются основные особенности местности, проверяет поверхность локально, используя окно 3 x 3. Это упрощение впервые использовано в ГИС ESRI Arc/Info. Ячейка в растровой DEM имеет восемь соседей, образующих четыре тройки (рисунок 10.8-а).

 

Для каждой тройки ячеек по соответствующей вариограмме рассчитывается коэффициент вариации (рисунок 10.8-б). Первая тройка имеет нулевой коэффициент вариации, вторая и четвертая – низкий, а третья – высокий коэффициент вариации. Далее оценивается средняя вариация значения узла растровой DEM. Узлы с высокими показателями вариации включаются в результирующее разбиение, остальные отбрасываются.

 

Третий алгоритм выбора точек триангуляции основан на оптимизации существующего разбиения. Для заданной растровой DEM требуется найти такое подмножество точек (заданной мощности), что при соединении их линиями в треугольники получится как можно лучшее представление поверхности.

По узлам регулярной сети легко построить исходное разбиение на треугольники. В начале работы алгоритма разбиение полностью соответствует исходной растровой DEM. Далее все точки разбиения поочередно проверяются следующим способом. Точка временно удаляется, соответственно изменяется и разбиение. Затем определяются треугольники, содержащие удаляемую точку, оценивается разность возвышений этой точки, полученных из DEM и из трех верши треугольника. Эта разность записывается в базе данных и удаленная точка восстанавливается. Когда таким образом будут обработаны все точки, нужно удалить точки с наименьшими значениями запомненных в базе данных разностей.

После того, как выбрано необходимое количество узлов TIN, нужно выбрать способ разбиения поверхности на треугольники. При этом желательно получить близкие к равносторонним треугольники, чтобы произвольная точка поверхности была как можно ближе к узлам TIN, где значения возвышения известны точно. Рассмотрим два способа разбиения на треугольники.

 

 

Триангуляция может быть получена путем упорядочивания точек по расстоянию между ними. Для этого вычисляются и сортируются по возрастанию расстояния между всеми парами точек. Ближайшие пары точек соединяются линией, если эта линия не пересекает полученные на предыдущих шагах линии. Процесс завершается, когда невозможно создать ни одной новой линии. В результате получится TIN-разбиение, в котором будет много остроугольных треугольников.

 

Этого недостатка лишена триангуляция Делоне. По определению три точки формируют треугольник в триангуляции Делоне тогда и только тогда, когда в окружности, описанной вокруг этого треугольника нет других точек разбиения. Разобьем поверхность на области, в которых каждая точка расположена ближе всего к некоторому узлу сети – генерирующей точке. Полученные границы называют полигонами Тиссена или полигонами Вороного.

Две точки соединяются линией в триангуляции Делоне, если их полигоны Тиссена имеют общую границу. Этот метод позволяет получить требуемые “жирные” треугольники.

 

 

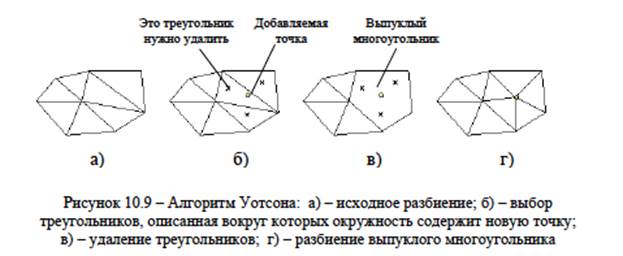
Триангуляция Делоне может быть получена при помощи алгоритма Уотсона. В начале работы этого алгоритма создается супертреугольник, содержащий все точки разбиения. Точки последовательно добавляются в существующее разбиение. Опишем процедуру образования нового разбиения придобавлении новой точки (рисунок 10.9). Сначала выбираются треугольники, описанная вокруг которых окружность содержит добавляемую точку. По определению эти треугольники не могут входить в триангуляцию Делоне, поэтому их следует удалить из разбиения. Выбранные треугольники разбиваются на отрезки, дублирующиеся отрезки удаляются. Оставшиеся отрезки формируют границу выпуклого многоугольника, который разбивается на новые треугольники простым соединением вершин с добавляемой точкой. По окончании работы алгоритма супертреугольник удаляется.

 

Существует два основных способа хранения TIN: по треугольникам и по точкам. При кодировании сети по треугольникам для каждого треугольника в базе данных создается запись, содержащая его уникальный номер, координаты трех его вершин, а также номера трех смежных с ним треугольников (рисунок 10.10-а). Во втором способе (рисунок 10.10-б) для каждой точки разбиения сохраняется ее уникальный номер, координаты и список точек, с которыми она соединена прямыми (по часовой стрелке).

 

По растровым DEM и по триангуляционным сетям можно построить

карты распределения характеристики по территории. Для этого нужно задать

список значений z, по которым будут проведены изолинии. Например, можно

взять максимальное и минимальное значения характеристики, разделить по-

лученный интервал на несколько частей и с полученным шагом провести

изолинии.

 

Вопрос № 8