Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Топологические отношения в пространственном анализе.Содержание книги
Поиск на нашем сайте
Топологические отношения в ГИС позволяют описывать связанность и отделимость точек или линий, определяющих взаимосвязи объектов в слое. Топологические отношения являются одним из наиболее полезных видов отношений, поддерживаемых пространственными базами данных. Топологическая структура данных определяет, где и как точки и линии соединяются в узлах на карте. Порядок соединения определяет форму дуги или полигона. Рассмотрим пример кодирования топологических связей в ГИС и топо- логию «дуга-узел». После того, как векторизованы объект карты и построена топология, возможно определять связанность объектов, например, с какими полигонами соседствует полигон А, какой полигон граничит с полигоном Б через границу d, найти все возможные пути из третьего узла во второй. Топология объектов может быть построена по «спагетти» следующим образом. Объекты и атрибуты позволяют описывать условия, существующие на карте или в реальности. Векторные объекты, используемые для описания пространственного изменения явления должны подчиняться правилам: два площадных объекта не должны перекрываться и каждая точка изучаемого пространства должна находиться внутри только одного площадного объекта.
Если редактируются точки объектов слоя, топология должна быть построена заново. Построение топологии включает в себя вычисление и кодирование взаимосвязей между объектами на основе планарных правил, использующихся для построения объектов по оцифрованным линиям. Планарные правила позволяют исправлять ошибки, возникающие при оцифровке. В модели топологических отношений Эгенхофера формализуются топологические отношения, которые могут существовать между двумя пространственными объектами. Такие топологические понятия, как смежность, вложенность и д.р., описываются совокупностью пересечений между внутренностями, границами и дополнениями двух элементов. Топологическое отношение R между двумя элементами A и B может быть задано матрицей:
Значениями ячеек матрицы являются либо пустое значение
Если топологическое отношение между AX и BX в X эквивалентно то- пологическому отношению AY и BY в Y, то матрицы пересечений инвариан- тов для этих отношений будут идентичны. Обратное не верно, идентичность матриц пересечений инвариантов не означает эквивалентности отношений. Описанная модель топологических отношений полностью описывает про- странственные отношения между объектами на уровне констатации факта отношения, но не содержит средств описания характера отношения. Напри- мер, если два региона касаются в двух точках, в модели будет зафиксирован только факт касания. Вопрос № 9
|
|||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 1072; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.177.65 (0.009 с.) |



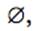 , озна- чающее, что сравниваемые внутренности, границы или дополнения не пере- секаются, либо непустое значение
, озна- чающее, что сравниваемые внутренности, границы или дополнения не пере- секаются, либо непустое значение 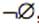 , если в пересечении имеется хотя бы одна точка. Различные комбинации значений ячеек матрицы описывают 512 различных топологических отношений. Любое пространственное отношение между двумя элементами является инвариантом одного из отношений, опи- сываемых матрицей. Однако на плоскости возможно реализовать лишь часть этих отношений (рисунок 3.2).
, если в пересечении имеется хотя бы одна точка. Различные комбинации значений ячеек матрицы описывают 512 различных топологических отношений. Любое пространственное отношение между двумя элементами является инвариантом одного из отношений, опи- сываемых матрицей. Однако на плоскости возможно реализовать лишь часть этих отношений (рисунок 3.2).