
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных уравнений. Метод Гаусса. Контроль точности при решении. Метод простой итерации, условие сходимости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
СЛАУ используются для описания дескриптивных моделей. Т.о. СЛАУ имеет след.вид:
Метод Гаусса относится к точным методам решения СЛАУ
На первом шаге 1е ур-е делится на На втором шаге из эл-тов 2го ур-я вычитаем эл-ты первого, умноженные на а21, получаем ур-е a’22x2+a’23x3=a’24. Произведем n операций умножения. Из элементов третьего ур-я вычитаем эл-ты 1го, умнож.на коэф-ты а31. Получаем ур-е a’32x2+a’33x3=a’34. Коэф-ты 2го и 3го ур-я вычисляются по формуле: При этом мы проделываем n2 операций умн.и дел. Работаем с полученной системой. На третьем шаге 2е ур-е делим на а22
На четвертом шаге: 3е-2е На пятом шаге: 3е\
Эти 5 шагов носят название прямого хода метода Гаусса. Обратный ход заключается в получении значений неизвестных по этой матрице. Точность метода: применяется метод контрольных сумм для проверки потери точности. Для этого в исх.матрицу добавляется еще один столбец, эл-ты к-го вычисляются по формуле:
Но контролировать на каждом этапе решения невозможно, поэтому вычисляют дополнительную неизвестную
Между основными и дополнительными переменными должно соблюдаться: Но реально такого быть не может, поэтому вводится точность 𝛆. Разница между основным и дополнительным x должна удовлетворять следующему: 1. На 1м шаге 2. Для каждого ур-я считаем 3. Решаем новую систему методом Гаусса. 4. Получаем решение 5. Окончательно имеем результат Тем самым для достижения приемлемой точности мы специально идем на потерю времени, решая дважды систему методом Гаусса. Мало того, проверка и восстановление точности может происходить циклически несколько раз. Метод простой итерации. МПИ-это приближенный алгоритм решения СЛАУ. Предположим, что исходная система АХ=В каким-либо образом приведена к виду: Х=CX+F, при этом заданы начальные значения искомых переменных. Начальные значения берутся исходя из смысла задачи. Данное нач.зн-е мы подставляем в правую часть системы вида Х=СХ+F. Тем самым получаем новый вектор Этот процесс является сходящимся к искомому решению, если выполняется следующее неравенство:
МПИ явл приближенным методом решения, применяется довольно редко ввиду наличия условия сходимости, сходится довольно быстро, обычно не превышает n итераций, n – кол-во переменных.
|
||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 AX=B
AX=B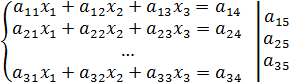 ∆≠0→решение есть и оно единственное
∆≠0→решение есть и оно единственное , получаем ур-е вида
, получаем ур-е вида  , где b1j = a1j/a11, где j=2,3,4. В общем случае на первом шаге получаем n оп.деления
, где b1j = a1j/a11, где j=2,3,4. В общем случае на первом шаге получаем n оп.деления
 0:
0: ,
, 
 ,
,  ,
, 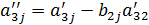 , j=3,4
, j=3,4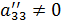
 - система треугольного вида, где коэф-ты ниже главной диагонали =0.
- система треугольного вида, где коэф-ты ниже главной диагонали =0. , где i=1,2,3. При прямом ходе метода Гаусса с эл-ми этого столбца производятся все те же действия, к-е производятся со строками, на любом этапе должно соблюдаться равенство:
, где i=1,2,3. При прямом ходе метода Гаусса с эл-ми этого столбца производятся все те же действия, к-е производятся со строками, на любом этапе должно соблюдаться равенство:  . После прихода к треугольному виду должны выполняться равенства:
. После прихода к треугольному виду должны выполняться равенства: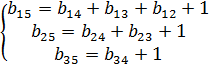
 , только в кач-ве столбца своб.членов выступает дополнительный столбец. Получаем систему:
, только в кач-ве столбца своб.членов выступает дополнительный столбец. Получаем систему:

 . Если равенство верно, то ответ получен с точностью до 𝛆. Если нет – произошла потеря точности мы попытаемся её восстановить:
. Если равенство верно, то ответ получен с точностью до 𝛆. Если нет – произошла потеря точности мы попытаемся её восстановить: обозн как
обозн как 
 - невязка, их подставляем в исх систему в кач-ве столбца своб членов.
- невязка, их подставляем в исх систему в кач-ве столбца своб членов. - поправки
- поправки
 . На след.шаге вектор
. На след.шаге вектор  подставляется в правую часть системы
подставляется в правую часть системы  , получаем
, получаем  , аналогично делаем до тех пор, пока разность между значениями всех Хi на каком-то шаге не будет отличаться от значений Хi на предыдущем (к-1) шаге на величину
, аналогично делаем до тех пор, пока разность между значениями всех Хi на каком-то шаге не будет отличаться от значений Хi на предыдущем (к-1) шаге на величину  :
: 

 - погрешность решения
- погрешность решения


