
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие численного интегрирования. Нахождение интеграла методом прямоугольников, методом трапеций, методом Симпсона.Содержание книги
Поиск на нашем сайте
1. F можно определить только для узкого круга ф-ций 2. Затраты на получение F(x) мб очень велики 3. Ф-я f(x) мб задана таблично Поэтому используется численное интегрирование. Пусть f(x) – вещественная ф-я, определенная на На каждом маленьком инт выберем Сумма S без предела – пример численного интегрирования, поскольку сумма отличается от истинного значения интеграла, можем оценить
Формул числ.интегрирования много, они отличаются друг от друга: 1) Выбором точек 2) Скоростью сходимости 3) Оценкой погрешности В общем случае точки S=Q+R, R – погрешность вычисления интеграла, квадратурная формула. Считается, что она задана, если известно, как выбираются узлы в весах, и как считается погрешность R. Метод прямоугольников. Отрезок
Каждый
От маленького отрезка можно перейти к R= Чем меньше шаг, тем выше точность. Метод трапеций.
На каждом отрезке R=
R= Метод Симпсона.

Строим Для тог, чтобы посчитать a,b,c вычислим:
f( Значения должны совпадать с Составим сумму:
Отсюда можем записать
R= На практике при выборе h для достаточно большого [a;b] необходим о выбрать максимальное знач шага таким образом,чтобы мы смогли вычислить площадь с заданной точностью. Метод прямоугольника:
Метод трапеции:
Метод Сипсона:
В зав-ти от
Решение обыкновенных дифференциальных уравнений. Методы решения. Задача Коши. Краевая задача. Решение ОДУ методом Эйлера, модифицированным методом Эйлера, методом Рунге – Кутта, методами прогноза и коррекции. Решение ОДУ большого порядка. Решение систем ОДУ. Методы решения краевых задач. Ур-ния, содержащие неизвестную ф-цию под знаком производной, называются дифференциальными уравнениями. Если ур-ние содержит одну независимую переменную и производную по ней, то оно называется обыкновенным, т.е. ОДУ. Решить ОДУ – это значит найти некоторую ф-цию, которая удовлетворяла бы как самому ур-нию, так, возможно, дополнительным условиям. В зависимости от дополнительных условий различают задачу Коши и краевую задачу. Для решения задачи Коши существует набор хорошо апробированных методов, а решение каждой отдельной краевой задачи может потребовать специфических подходов. Поэтому в классической вычислительной математике рассматривают вычисления задачи Коши, которую в простейшем случае можно рассмотреть следующим образом: Задано ОДУ первого порядка: Решение: 1).x1=x0+h; 2)tgα=f(x0,y0); 3)y=y0=tgα(x-x0); 4)x=x1, y=y1; 5)x1y1 Численные методы для решения этой задачи могут быть разбиты на две группы: одношаговые и многошаговые. Одношаговый метод. В основе всех одношаговых методов лежит разложение ф-ций в ряд Тейлора:
y(x+h)=y(x)+hy’(x)+O(h2)
В результате имеем общую формулу метода Эйлера: Несомненное преимущество метода Эйлера – простота реализации. Существенный недостаток – крайне низка точность, которую, однако, можно заранее оценить.(с каждым шагом глобальная погрешность увеличивается) Как правило, для повышения точности осуществляют решение с шагом h, с шагом h/2 и т.д. В этом случае процедуру называют самоконтролирующей или с автоматическим выбором шага. Все остальные одношаговые методы базируются на идее Эйлера, но для значительного повышения точности используются дополнительные точки. Модифицированный метод Эйлера:
3)tg α1=f(x1,y1) 4) tg αср= (tg α0- tg α1)/2 5)y=y0+ tg αср(x-x0) 6)x=x1 след. y1ср; 7)x1,y1ср Точка по модиф. мет. Эйлера гораздо ближе к искомой, чем точка по обычному мет. Эйлера. Классическим считается метод Рунге-Кутта четвертого порядка точности. yn+1=yn+1/6(k0+2k1+2k2+k3) k0=hf(xn;yn) k1=hf(xn+1/2h;yn+1/2k0) k2=hf(xn+1/2h;yn+1/2k1) k3=hf(xn+1/2h;yn+k2) δ= |yn(h)-yn(h/2)|/15 Ошибка пропорциональна O(h5). Этот метод сочетает простоту реализации с достаточной
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.110.145 (0.008 с.) |

 . Геометрический смысл: если ф-я непрерывна на
. Геометрический смысл: если ф-я непрерывна на  , и мы можем найти её первообразную F, то используется формула Ньютона-Лейбница
, и мы можем найти её первообразную F, то используется формула Ньютона-Лейбница 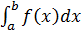 =F(b)-F(a). Но дело в том, что:
=F(b)-F(a). Но дело в том, что: ,
, 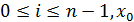 =a,
=a,  =b
=b ,
, 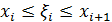 , и составим сумму:
, и составим сумму:  .
.  , если предел существует.
, если предел существует. ,
,  и
и  - верхняя и нижняя суммы Дарбу,
- верхняя и нижняя суммы Дарбу,  ,
, 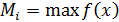 .
. ,
, 
 и
и  - весы, весы не зависят от f(x). Тогда можно составить:
- весы, весы не зависят от f(x). Тогда можно составить:  )
)

 , строим в этой точке прямую и находим точку её пересечения с f(x), проводим прямую FG, заменяем площадь ABCD на площадь AFGD. Мы можем записать:
, строим в этой точке прямую и находим точку её пересечения с f(x), проводим прямую FG, заменяем площадь ABCD на площадь AFGD. Мы можем записать: 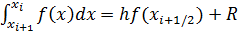
 ,
, 
 +
+ 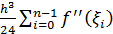
 ,
, 
 =h>0, f(x) принадлежит с2
=h>0, f(x) принадлежит с2 


 ,
, 




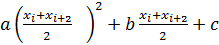
 f(
f( 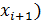 +
+  =
=  /
/ f(
f( 

 ,
, 


 считаем h. Это знач h выбирается исходя из нахудшего поведения f(x) на
считаем h. Это знач h выбирается исходя из нахудшего поведения f(x) на  и начальное условие: y(x0)=y0. Требуется найти ф-цию, удовлетворяющую как уравнению, так и начальному условию.
и начальное условие: y(x0)=y0. Требуется найти ф-цию, удовлетворяющую как уравнению, так и начальному условию. , в котором сохраняются члены до установленного порядка. Если сохраняется член вида
, в котором сохраняются члены до установленного порядка. Если сохраняется член вида  , то говорят, что метод имеет порядок n, а погрешность метода пропорциональна hn+1. Для нахождения следующей точки y(xk+1) требуется информация только об одной предыдущей точке y(xk) – способность самостартования.
, то говорят, что метод имеет порядок n, а погрешность метода пропорциональна hn+1. Для нахождения следующей точки y(xk+1) требуется информация только об одной предыдущей точке y(xk) – способность самостартования. Простейшим представителем одношаговых методов является метод Эйлера.
Простейшим представителем одношаговых методов является метод Эйлера.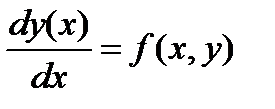
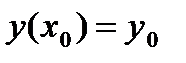


 y(x0)=y0, k=0,1,2,…
y(x0)=y0, k=0,1,2,…



