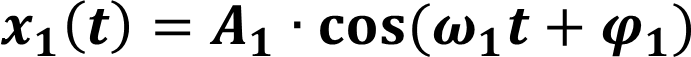Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Добротность колебательной системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Добротность колебательной системы, отношение энергии, запасённой в колебательной системе, к энергии, теряемой системой за один период колебания. Добротность характеризует качество колебательной системы, т.к. чем больше Д. к. с., тем меньше потери энергии в системе за одно колебание. Д. к. с. Q связана с логарифмическим декрементом затухания d; при малых декрементах затухания Q " p/d. В колебательном контуре с индуктивностью L, ёмкостью C и омическим сопротивлением R Д. к. с.
где w — собственная частота контура. В механической системе с массой m, жёсткостью k и коэффициентом трения b Д. к. с.
Добротность — количественная характеристика резонансных свойств колебательной системы, указывающая, во сколько раз амплитуда установившихся вынужденных колебаний при резонансе превышает амплитуду вынужденных колебаний вдали от резонанса, т. е. в области столь низких частот, где амплитуду вынужденных колебаний можно считать не зависящей от частоты.
40) Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы.
Решение уравнения:
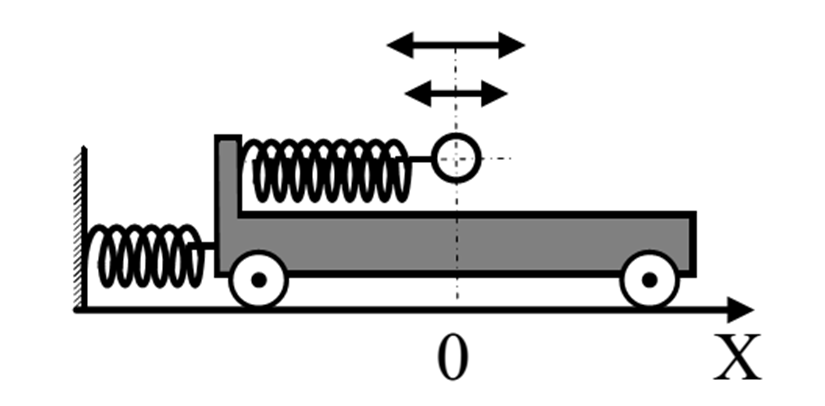
Резонанс(фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Амплитуда и фаза(не нашёл) 41) Сложение колебаний в одном направлении Уравнение движения шарика:
Уравнение движения тележки:
Бие́ния — явление, возникающее при наложении двух периодических колебаний, например, гармонических, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Частота изменения амплитуды суммарного сигнала равна разности частот исходных сигналов. Фигуры Лиссажу Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу.
42) Уравнение плоской волны. Фазовая скорость. Волновое уравнение. Решение волнового уравнения для плоской и сферической волны. Принцип суперпозиции.
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.219.131 (0.009 с.) |


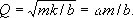
 -уравнение вынужденных колебаний
-уравнение вынужденных колебаний



 (на счёт решения и самого уравнения не уверен полностю)
(на счёт решения и самого уравнения не уверен полностю)