
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следствия 2-го закона НьютонаСодержание книги
Поиск на нашем сайте
1. Принцип причинности – имеется однозначная связь между изменением состояния движения материальной точки (тела) и действующими на эту материальную точку (тело) силами; 2. Принцип независимости действия сил – (в классической механике) каждая из действующих сил изменяет движение материальной точки (тела) независимо от действия других сил. Это позволяет рассматривать результирующую силу в виде линейной суперпозиции всех действующих сил.
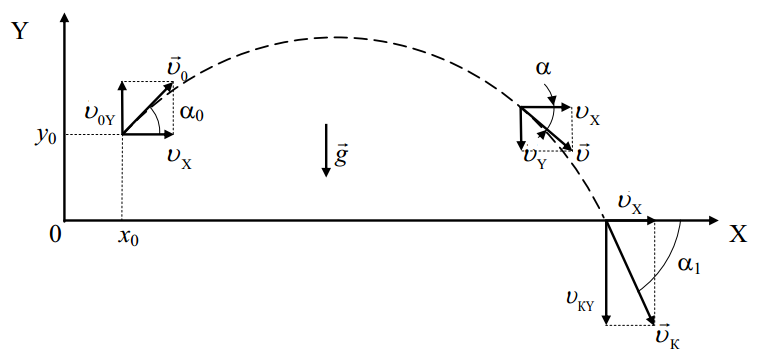
.4.Суперпозиция перемещений. Уравнение движения тела, брошенного под углом к горизонту.
5.Энергия. Примеры. Единица измерения. Кинетическая и потенциальная энергия в механике. Закон сохранения энергии в механике. Работа силы. Единица измерения работы. Мощность. Единица измерения мощности. Энергия Примеры энергии:
Кинетическая энергия связана с движением тела, она зависит только от массы и скорости движения тела по отношению к системе отсчета:
Потенциальная энергия определяется взаимным расположением тел и характером сил взаимодействия между ними. По названию понятно, что это то, что потенциально может перейти в другой вид энергии (например, в кинетическую энергию). Примеры:
2. Растянутая пружина Закон сохранения энергии: В системе, между которыми действуют только консервативные силы полная механическая энергия сохраняется, т.е. не изменяется со временем:
Работа силы – количественная характеристика процесса обмена энергией между взаимодействующими телами. Размерность работы: 1 Дж = 1 Н·м Мощностью называется отношение работы ко времени, за которое она совершается:
Мгновенная мощность:
Мощность измеряется в Ваттах (Вт): 1Вт = 1 Дж/с 6.Кинематика вращательного движения. Цилиндрическая система координат. Угловая скорость, угловое ускорение. Основное уравнение кинематики вращательного движения. Момент инерции, момент силы, момент импульса. Единицы измерения. Момент инерции тонкостенного цилиндра. Теорема Штейнера..Основное уравнения динамики для вращательного движения. Кинетическая энергия вращающегося тела. Закон сохранения момента импульса.
Для описания вращательного движения вводят следующие понятия:
Угол перемещения одинаков для всех радиус-векторов любой точки тела.
R – радиус (расстояние от центра вращения) φ – угол поворота относительно оси Угловая скорость (рад/с): Угловое ускорение (рад/с2):
Если скорость вращения постоянна ( · Основное уравнение кинематики вращательного движения
· Моментом силы
Модуль момента силы:
где
· Момент силы относительно оси – скалярная величина, равная проекции на эту ось вектора момента силы относительно произвольной точки на оси. Единица измерения момента сил –
· Моментом импульса Модуль момента импульса точки: Момент импульса твердого тела (системы материальных точек) относительно оси z:
· Моментом инерции материальной точки ( кг×м2)относительно оси вращения называется произведение массы этой точки на квадрат расстояния от оси: · Моментом инерции системы точек (тела) относительно оси вращения называется физическая величина, равная сумме моментов инерции составляющих его материальных точек:
· Момент инерции тонкостенного цилиндра Рассмотрим тонкостенный цилиндр постоянной плотности у которого ось вращения проходит через центр инерции:
где
Момент инерции элемента
Откуда получаем:
поскольку
· Теорема Штейнера момент инерции тела относительно произвольной оси
При действии момента силы на тело происходит изменение его кинетической энергии. Из этого можно получить:
Где Если ось вращения, совпадает с главной осью вращения, то мы получаем основной закон динамики вращательного движения:
· Кинетическая энергия вращения Если абсолютно твердое тело вращается вокруг оси
где
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 844; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.247.250 (0.008 с.) |

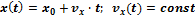
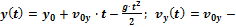 g
g 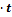
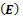 – универсальная мера различных форм движения и взаимодействия материальных тел и полей.(ДЖ)
– универсальная мера различных форм движения и взаимодействия материальных тел и полей.(ДЖ) )
)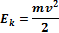
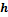
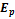 =
= 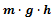
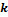 – коэффициент
– коэффициент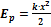
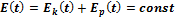
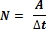
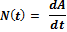

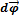 (направление по правилу буравчика)
(направление по правилу буравчика)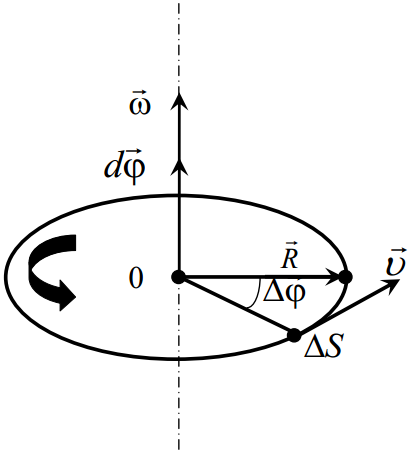 Полярные координаты:
Полярные координаты: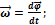
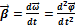
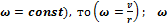 =
= 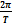
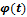 =
= 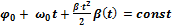
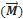 относительно точки (Н*м)называется величина, определяемая векторным произведением радиуса-вектора, проведенного из точки О в точку А (приложения силы) на силу:
относительно точки (Н*м)называется величина, определяемая векторным произведением радиуса-вектора, проведенного из точки О в точку А (приложения силы) на силу: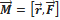
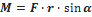
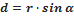 - плечо силы
- плечо силы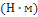
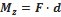
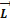 относительно неподвижной точки ( кг×м2/с.)называется физическая величина, определяемая векторным произведением радиуса-вектора на импульс:
относительно неподвижной точки ( кг×м2/с.)называется физическая величина, определяемая векторным произведением радиуса-вектора на импульс: 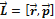
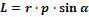
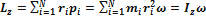
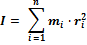
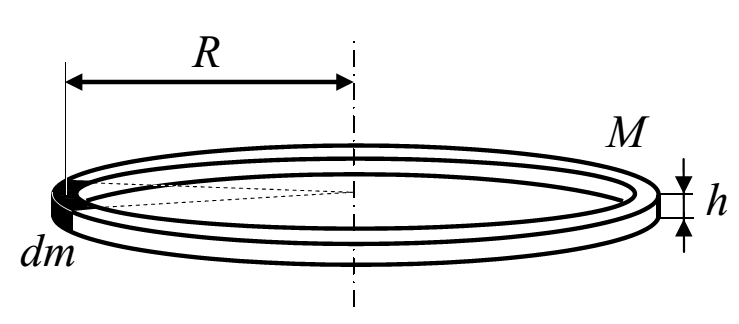
 – расстояние от оси вращения до стенки цилиндра;
– расстояние от оси вращения до стенки цилиндра;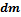 – элемент массы цилиндра
– элемент массы цилиндра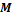 – общая масса цилиндра.
– общая масса цилиндра.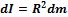
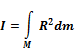
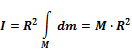
 равен сумме момента инерции относительно параллельной оси, проходящей через центр масс тела
равен сумме момента инерции относительно параллельной оси, проходящей через центр масс тела 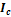 и произведения массы тела на квадрат расстояния между осями (
и произведения массы тела на квадрат расстояния между осями (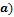 :
: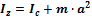
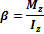
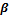 – угловое ускорение относительно оси
– угловое ускорение относительно оси 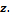
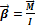 или
или 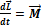
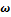 , то кинетическая энергия:
, то кинетическая энергия: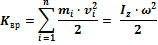
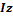 – момент инерции относительно оси
– момент инерции относительно оси 


